基于多元回归方法的岩石物理性质预测模型研究*
2018-09-18陈小根武立岐
陈小根 武立岐
(北京科技大学土木与资源工程学院)
为了在岩石中设计结构,钻孔作业是必不可少的环节。通过钻孔了解地层地质情况,对工程设计有指导意义,同时用于矿区岩石开挖工程所需的爆破炮孔也要通过钻孔作业完成,钻孔作业费用在工程预算中占较大的比重。所以,在钻孔作业之前,一般需要清楚岩石的完整性质,比如所钻地层岩石强度、密度等参数,从而确定施工技术和施工方案。获取岩石性质的传统方式是取芯,由实验测定。由于直接法耗费比较大,还有局限性,所以对岩石性质预测的间接法引起了一些学者[1-3]的兴趣。间接法不仅可用于确定完整的岩石性质,而且可以用于检验试验结果。
许多研究人员已经间接地定义各种岩石的性质采用不同的方法确定[4-8]。Kahraman等[9-11]研究在钻进过程中岩石的声的识别,利用傅立叶变换在旋转钻进过程中获得的声波信号控制岩石破碎过程。Vardhan等[12-13]在实验室通过改变钻头施加的推力和抗压强度,尝试用声级的变化确定岩体性质。通过科学方法将钻进参数和岩石物理性质建立起联系,对于岩石钻进工程优化、机械选择、耗损降低、工作效率提高都有重要意义。
本文通过室内钻进实验数据,利用多元回归的方法,建立钻进参数与岩石物理性质的数学模型,用于岩石物理性质的预测,并对模型进行验证。
1 岩石物理性质分析
岩石单轴抗压强度σ是经常使用的力学参数,是指试样只在一个方向受压时所得的极限粉碎强度,也就是说将岩石试样放在压力机的上下压板之间进行加压,直至试样被压坏时测得的压力强度值。一般利用单轴抗压强度仪器来测定。
纵波在岩石中传播的速度VP是地球物理勘探中常用的参数,它通常使用在现场和实验室来表征和确定岩石的动力性质。纵波速度可以在实验室中直接或间接测量。
岩石的密度ρ与岩石组成矿物及岩石的结构有关[14]。按岩石含水状态分为岩石天然密度和干密度。岩石密度对组成特定岩石类型的矿物非常敏感。一般用直接测量方法得出岩样的体积v,称出原岩样烘干质量m,然后求出岩石密度。
本次研究的目的是找出3个表征岩石性质的物理力学参数(σ,VP和ρ)和钻进过程中产生的声级水平之间的关系,建立估算模型,输入间接参数,预估出岩石的性质。
2 实验研究
2.1 实验的岩石样品
从现场获得的10种不同岩石样本包括板岩、石英岩、浅绿色石英岩、石榴石黑云岩、粉石英岩、绿石英岩、榴辉岩、黄色石英岩、烟熏石英岩、大理石。岩块尺寸为20 cm×20 cm×20 cm。
2.2 实验装置
在实验室采用BMV45 T20型计算机数控(CNC)垂直加工中心(图1)进行岩石样品钻进实验。用于钻进作业的刀柄长40 mm,硬质合金钻头直径为6,10,16和20 mm,钻孔长30 mm。由于钻进方法会影响产生的声音,在整个钻进过程中,为了获得一致的数据,提供相对恒定的转速和穿透率。

图1 CNC垂直加工中心
2.3 A计权等效声级测定
在钻孔过程中,为了克服岩块的振动,用虎钳夹将岩石样品紧紧地固定在机器的台面上。
钻头直径为6,10,16和20 mm;钻头转速为150,200,250和300 r/min;钻速为2,3,4和5 mm/min。对于不同钻头直径、钻头转速和钻速的组合,总共得到64组试验条件,记录岩块64种不同的A计权等效连续声级(Leq)。对于所有的测量,声级计保持在距离钻头1.5 cm。对于一个特定的条件、同一块岩石,在相对快速的演替中,确定5次声级水平。结果发现,记录的等效声级几乎一致。5次测量算术平均作为计算一个特定条件的A计权等效声级值。
3 基于钻进过程声级的岩石参数预测
3.1 岩石参数及声级
从实验室测试和基本的统计评估,如均值、最大值、最小值的结果以及不同参数的标准偏差,随着范围(最大值和最小值)的A计权等效声级在钻井过程中完整的变质岩石记录见表1。对这些结果采用多元回归分析和方差分析(ANOVA)。岩石性质(σ,VP和ρ)与钻进过程的声级的关系见图2。
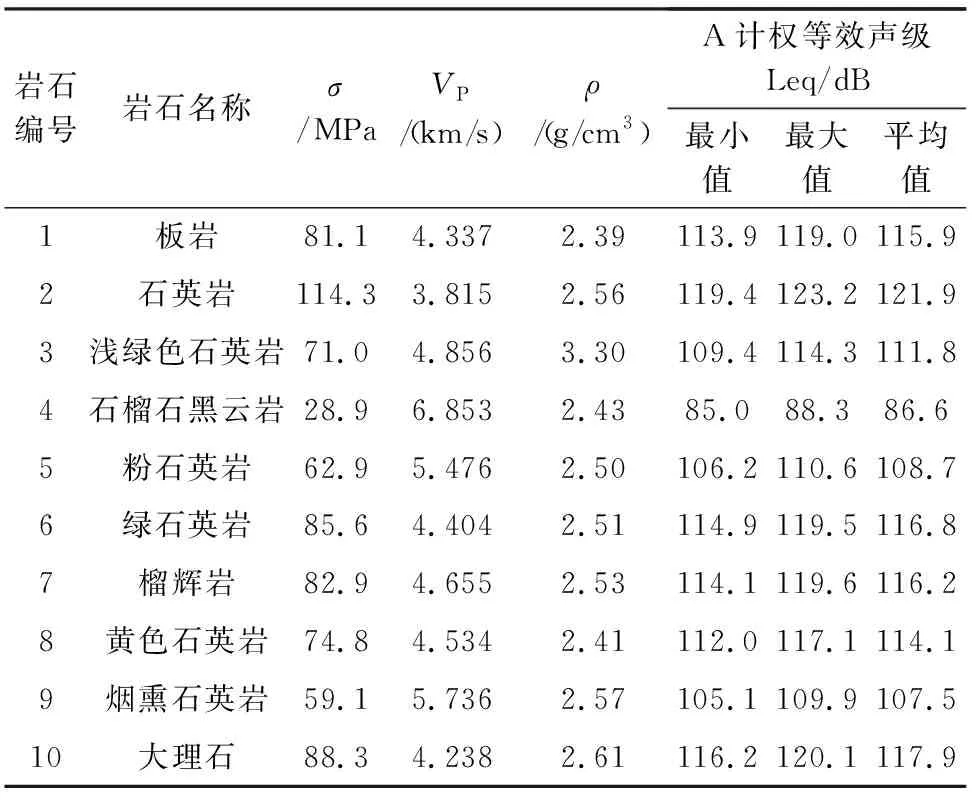
表1 岩石物理力学参数
从实验数据可以看出,岩石在不同工况下的等效声级与表征岩石特性的物理参数(σ,VP和ρ)之间表现出了良好的相关性。
3.2 基于声级的岩石参数预测模型
为了获得合适且实用的预测定性关系,需要对岩石物理力学性质和钻进过程变量参数进行建模。一个详细的过程表示可以预期一个二阶模型,通过在响应和相应的重要参数之间使用非线性拟合,采用多元回归方法对各种响应进行建模。模型的性能取决于以复杂方式起作用和相互作用的大量因素。
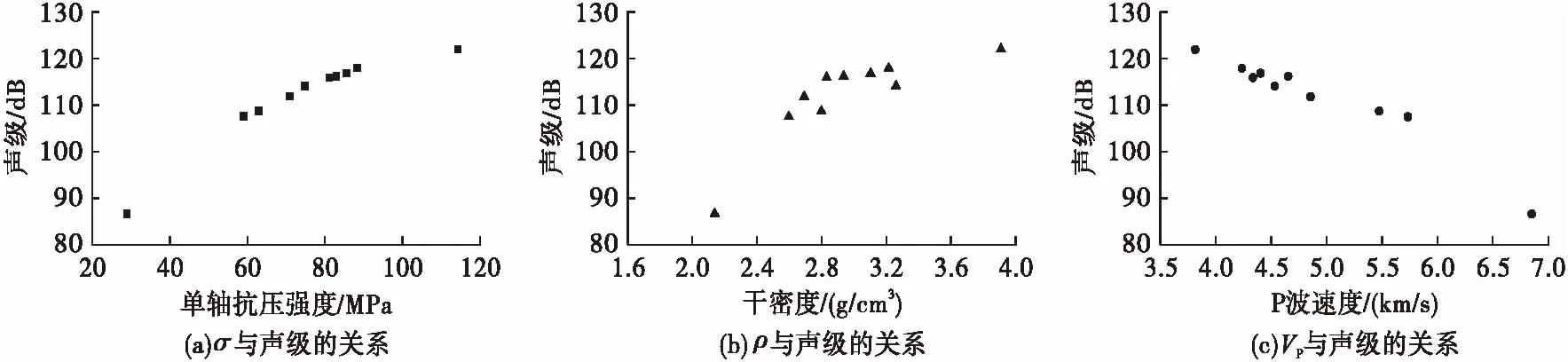
图2 岩石性质与声级的关系
钻进过程中产生的声级水平也受多种因素的影响,方差分析发现输入参数对期望响应有显著影响。为了便于实验和测量,本次研究除了考虑在钻进过程中产生的等效声级A(dB),还考虑3个重要因素,即钻头直径B(mm)、钻头转速C(r/min)、钻进速率D(mm/min)。对应所考虑的响应是单轴抗压强度σ、P波速度VP和干密度ρ。所考虑的物理力学性质参数的数学模型可以表示为
Y=f(x1,x2,x3,…,xn)+∈ ,
(1)
式中,Y为响应;x1,x2,x3,…,xn为独立变量;∈为拟合误差;f的二次模型可以表示为
(2)
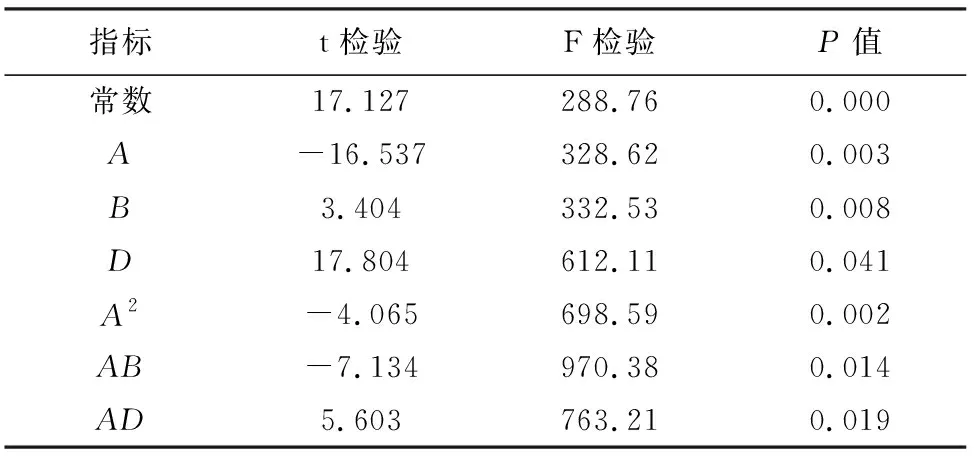
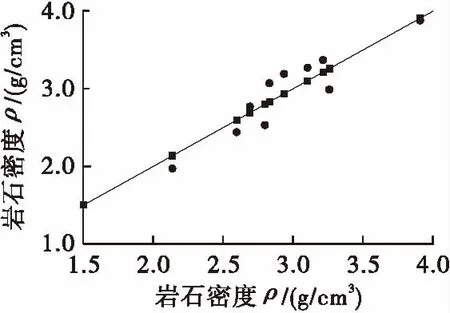
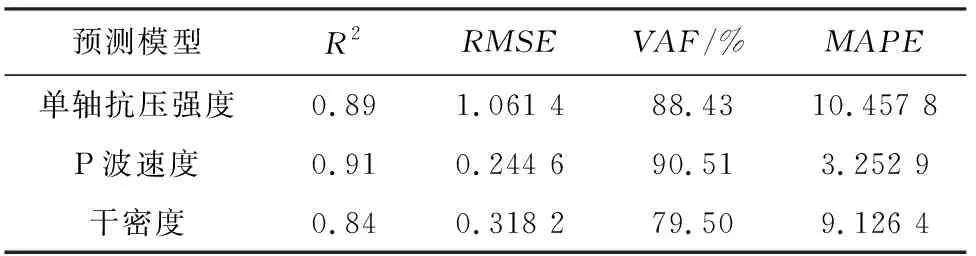
式中,ai为xi的线性效应;aij为xi的二次效应,aij(i 模型里响应面包含常数项、线性项、平方项和交叉乘积项。为了比较所有合理的回归模型,采用一种向后淘汰程序筛选。首先建立回归方程,然后对回归方程系数进行a水平(“经验法则”是将a设置为0.05,即95%置信区间)的t检验,如果t统计量在选定的a水平不显著,考虑的独立变量从模型中被删除,并且通过使用包含所有剩余独立变量的回归模型来执行回归分析;如果t统计量显著,则选择模型。通过选择具有绝对最小t统计量的自变量得到需要的回归方程,并对方程进行F检验,最后建立预测岩石特性物理力学参数的回归模型。 3.2.1 单轴抗压强度σ 单轴抗压强度σ最终建立的回归模型为 σ=543.142-12.080×A+1.876×B+0.065× C+0.071×A2-0.017×A×B-0.001×A×C. (3) 估算单轴抗压强度的回归模型的检验分析见表2。对于σ,独立变量A、B和C的P值都小于0.05,具有统计学意义。除此之外,A2的P值以及B、C与A有关的交互项AB和AC的P值都小于0.05,从而建立了实验结果。 表2 σ估计的回归模型检验分析 将自变量代入到回归模型中,得到单轴抗压强度的预测值,在同一个图中绘制出预测值与实测值,见图3。 图3 单轴抗压强度预测值与实测值●—预测值;■—实测值 3.2.2 P波速度VP P波速度回归模型为 VP=-1.192 6+0.223 6×A-0.025 56×B- 0.001 3×B2-0.014×A2+0.000 56×A×B. (4) 估算P波速度的回归模型的检验分析见表3。对于VP,独立变量A、B的P值都小于0.05,具有统计学意义。除此之外,A2、B2的P值以及B与A有关的交互项AB的P值都小于0.05,从而建立了实验结果。 表3 P波速度估计的回归模型系数分析 将自变量代入到回归模型中,得到P波速度的预测值,在同一个图中绘制出预测值与实测值,见图4。 图4 P波速度预测值与实测值●—预测值;■—实测值 3.2.3 干密度ρ 干密度ρ最终模型为 ρ=19.336-0.392 4×A+0.074 7×B+ 0.063 6×D+0.002 2×A2-0.000 8× A×B-0.000 56×A×D. (5) 估算干密度的回归模型的检验分析见表4。对于ρ,独立变量A、B、D的P值都小于0.05,具有统计学意义。除此之外,A2的P值以及B、D与A有关的交互项AB和AD的P值都小于0.05,从而建立了实验结果。 表4 干密度估计的回归模型系数分析 将自变量代入到回归模型中,得到干密度的预测值,在同一个图中绘制出预测值与实测值,见图5。 图5 干密度预测值与实验值●—预测值;■—实测值 测量值与预测值之间的相关系数是检验模型预测性能的一个很好的指标。在本研究中,数值计算(VAF)和均方根误差(RMSE)指数是为了控制在研究中开发的预测模型预测能力的表现。 (6) (7) 式中,y和y′分别为测量值和预测值。 对于一个模型,若VAF为100,且RMSE为0,则该模型是优良的。平均绝对百分比误差(MAPE)是统计中拟合系列值精确度的测量值,也被用作模型的预测性能。MAPE通常以百分比表示准确性。 (8) 式中,Ai为实际值;Pi为预测值。 建立的回归模型的性能指标见表5。 表5 回归模型的性能指标 由表5可知,与单轴抗压强度和干密度模型相比,所开发的预测P波速度的模型更有效,其具有低的RMSE值和高的VAF值。这些值可用于将已开发模型的性能与其他间接调查进行比较。对于单轴抗压强度、P波速度、干密度,MAPE值分别为10.457 8,3.252 9,9.126 4,即模型的准确度分别为89.5%,96.7%,90.8%,这间接地说明了预测模型的可靠性。 在考虑钻头直径、钻头转速和钻进速度的影响下,研究及评价在钻井过程中产生的3个完整岩石特性和声级之间的经验关系。所开发的预测模型并不旨在替代ISRM建议的测试方法,而是作为一种快速而简单的方法来估计完整岩石的物理力学性质,其优点之一是可以通过一个实验来估计多个岩石性质。回归模型计算出的岩石特性值和实际值比较接近,表明所开发的模型可以得到有效应用,具有可接受的精度,在设计的初步阶段可以预测采矿行业的完整岩石性质。然而,需要进一步的研究来预测岩体的性质。
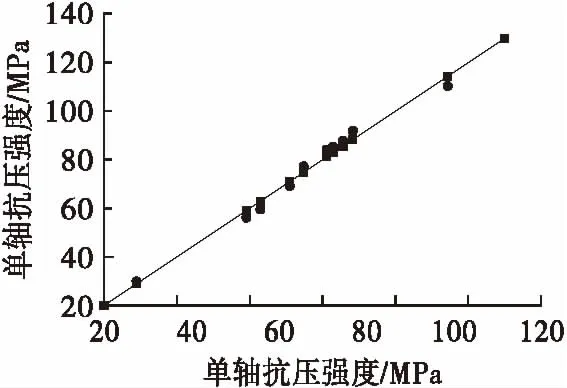

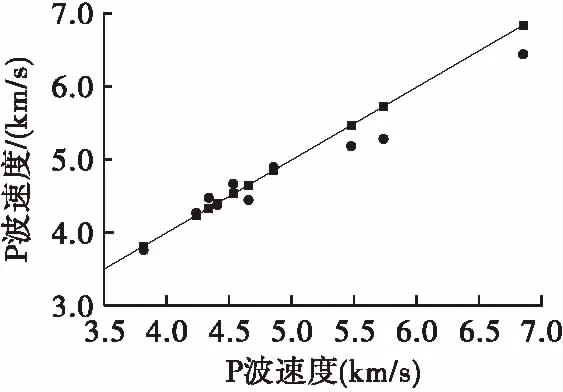
3.3 模型的预测性能
4 结 论
