基于应变能均化指标和云模型的结构损伤识别

郭惠勇，张鑫，王玉山

(1. 重庆大学 山地城镇建设与新技术教育部重点实验室；土木工程学院，重庆 400045；2. 石河子大学 水利建筑工程学院，新疆 石河子 832003)

工程结构在建成投入使用后，由于复杂服役环境下各种静动力荷载的长期作用，其材料的力学性能会发生相应退化，并累计起裂缝、变形等各种损伤，结构损伤经过长期积累会导致其整体性能降低，严重情况下会发生倒塌等灾难性事故。为了能够更早地发现结构性能的改变，进而采取必要手段最大限度地降低或避免危险的发生，有必要对结构的损伤进行识别。因此，对结构物进行损伤识别研究是目前研究的热点之一[1]。由于结构的模态等动力参数对结构的损伤较为敏感，故学者基于结构的模态等动力参数进行了大量损伤识别研究[2-3]。Koh等[4]利用模态相关性对悬索桥进行了损伤检测，Morassi等[5]构造了一个钢结构框架模型，用切口来模拟钢结构的损伤，使测试频率与结构模型的前几阶固有频率相吻合，在此基础上利用优化后的频率算法对结构进行损伤识别定位。刘济科等[6]提出了一种利用残余力向量进行结构损伤识别的两步法，通过计算结构单元的损伤定位标准值和最佳逼近向量法进行损伤的识别和定位。在这些模态参数中，模态应变能包含有振型信息，是一种较为有效的动力参数。Shi等[7]采用模态应变能变化率指标进行了损伤定位检测。Sazonov等[8]提出了应变能振动基损伤识别方法，进行了损伤定位识别。刘晖等[9]建议了可以同时定位和定量的应变能耗散率指标方法。郭惠勇等[10-11]采用应变能耗散率方法与贝叶斯理论相结合，对结构的损伤定位进行研究，并提出了一种应变能等效指标方法。Hu等[12]提出了模态分析和微分求积法计算应变能，并对复合材料板的裂纹损伤进行了识别研究。Seyedpoor[13]提出了一种两阶段的检测结构损伤的方法，该方法先采用模态应变能进行损伤定位，再利用粒子群优化算法进行二次识别。目前，现有的应变能损伤指标方法难于处理随机测量噪声引起的不确定性问题，需要寻找相应的不确定处理策略。云模型具有处理不确定性问题的能力，是Li等[14-15]提出的一种定量和定性之间的转换模型，可以通过定量和定性的映射关系实现不确定传递。云模型已经广泛应用于图像处理、数据挖掘等领域，在土木工程领域的应用还比较少，具有一定的研究价值。笔者拟采用云模型方法处理噪声等引起的不确定性问题，并结合应变能进行损伤识别研究。

1 应变能均化指标

1.1 模态应变能

结构损伤可以引起振型等模态参数发生改变，而模态应变能不仅包含振型信息，还包含刚度信息，故模态应变能数据可以较好地反映结构的损伤状况，其对损伤的敏感性要好于单纯的振型数据。损伤前后结构的第j个单元和第i阶模态的模态应变能一般表达式如式(1)。

(1)

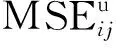
(2)

损伤前后的模态应变能数据是建立相应损伤识别指标的基础。

1.2 模态应变能耗散率指标和等效指标

从能量变化的角度分析，结构的损伤也可考虑为能量逐渐耗散的过程，刘晖等[9]利用模态应变能耗散率和变化率相等的原理推导出应变能耗散率方法，将其简称为应变能耗散率指标(Modal Strain Energy Dissipation Ratio Index, MSEDRI)，该指标可用来进行损伤的位置程度分析。第j个单元的模态应变能耗散率指标为[9]

(3)

郭惠勇等[11]借鉴了应变能耗散率方法，并利用能量等效原理，推导出一个能量等效方程，并通过分析结构损伤对模态应变能的变化趋势影响，从等效方程中提取了一种模态应变能等效指标(Modal Strain Energy Equivalence Index, MSEEI)，具体为

(4)

1.3 模态应变能均化指标

通过大量算例分析，发现应变能耗散率指标的值往往高于真实损伤值，而应变能等效指标的识别结果虽相对较好，但其值往往低于真实值。通过对两种指标分析可知，由于模态应变能耗散率指标在推导过程中为了简化计算而采用了损伤前的刚度替换损伤后的刚度，导致指标值往往大于真实损伤值，而应变能等效指标通过直接假设损伤后的刚度来建立模态应变能变化和等量耗散的等效方程，但未考虑能量耗散的过程效应，其指标往往低于真实损伤值。故两种指标具有一定互补的特性，可通过两种指标的均化建立一种新的指标。由Seyedpoor的研究[13]可知，损伤后单元刚度降低，而模态应变能却有增加的趋势，由以上两种指标的均化来确立一种新的模态应变能损伤指标，即模态应变能均化指标(Modal Strain Energy Mean Index, MSEMI)，可推导出该应变能损伤指标为

(5)

由于刚度损伤系数往往大于或等于0，故以上损伤指标更精确的表示形式为

MSEMIj=

(6)

该指标可以利用损伤前后的模态应变能数据进行损伤的定位和定量识别。但在实际应用中，测量噪声不可避免，获取的测量数据往往是含有随机噪声的不确定数据。单纯的应变能指标虽然可以较好地处理损伤识别的确定性问题，但对于含有随机噪声的不确定性问题，单纯的应变能指标难于有效处理。故提出一种云模型和应变能均化指标相结合的方法，来处理损伤识别的不确定性问题。

2 云模型和损伤识别处理策略

2.1 云模型和数字特征

云模型是对定量数据和用自然语言表示的定性概念之间的不确定性进行相互转换的模型，主要反映了客观世界事物或现象中概念的随机性与模糊性，并将随机性与模糊性完全集成在一起，为处理定性与定量相结合的不确定性问题提供了一个有效的解决途径。云模型的数字特征可以用来表征概念所具有的整体特性。云的数字特征包括期望Ex(Expectation)、熵En(Entropy)和超熵He(Hyper-entropy)，这3个数字特征的具体含义为[15]：期望(Ex)是在整个定量论域空间中能最大程度地代表这个定性概念的点，也就是云重心所在的位置；熵(En)这一数字特征既反映了代表这个定性概念的云滴的离散程度，也就是云滴在定性概念上的随机实现，又体现了定性概念C在定量论域U上的范围，又称作模糊性，即亦此亦彼性的裕度，通过熵可以看出随机性和模糊性两者之间相互关联的特征；超熵(He)是对熵不确定性的度量，也即熵的熵，这一数字特征体现了在定量论域U上对该定性概念C有贡献的所有点的不确定性的聚集程度，反映了确定度Δ(x)随机性的大小。

2.2 损伤识别处理策略

在实际测量中，模态数据会受到测量噪声的干扰，则包含模态数据的应变能同样也会受到测量噪声的干扰，从而使应变能损伤指标的识别结果产生较大偏差，并难于判断识别结果的可靠性。因此，单纯采用应变能的损伤指标难以处理噪声和误差等引起的不确定性问题，故利用云模型技术和模态应变能指标相结合来分析测量噪声和误差的干扰问题。

云模型中的云发生器作为云生成算法，可对含随机测量噪声的采样数据进行处理。云发生器包含正向和逆向云发生器，由定性概念向定量数值进行转化的发生器称为正向云发生器，由定量数值向定性转化的发生器为逆向云发生器。正向云发生器通过输入云模型的3个数字特征值，在发生器内生成满足条件的云滴，云滴数量达到一定程度时构成云；逆向云发生器通过输入一定数量的云滴，来得到云的3个数字特征值。笔者利用多次测量数据生成云滴，借鉴逆向云发生器产生云的数字特征，并进行损伤识别。

由统计理论，根据采样数据计算样本统计值。

样本均值

(7)

一阶样本绝对中心矩

(8)

样本方差

(9)

式中：N是采样次数。然后，根据云模型理论计算出期望、熵和超熵的估计值。

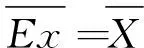
(10)

(11)

(12)

再利用期望、熵和超熵估计值计算确定度函数

(13)

基于以上算式，建立应变能均化指标和云模型相结合的损伤识别处理策略：

1)进行多次测量，获取相应的含随机测量噪声的模态数据；

2)利用模态数据计算相应的模态应变能以及模态应变能均化指标数据值，多次测量可以获取多组数据，从而可以构造出包含多个云滴的群；

3)计算所有云滴的数字特征，即期望、熵和超熵，并计算相应的确定度；

4)利用计算的期望进行含噪数据下的损伤位置识别，并进行云模型的确定度分析。

3 数值计算

二维桁架结构如图1所示，该桁架结构是损伤检测和识别常用的一个典型结构。其基本参数为：弹性模量E=7.2×104MPa，杆件截面面积A=0.001 m2，材料密度ρ=2 800 kg/m3，杆件长度如图1所示。该结构的有限元模型共有31个杆单元、14个节点、28个自由度。考虑约束作用，该模型有25个实际自由度。考虑两种多损伤工况；第1种工况，单元6和单元23发生损伤，刚度分别降低25%和30%；第2种工况，单元3、16、21发生损伤，刚度分别降低25%、35%和30%。由于实际应用中测量噪声不可避免，故测试的模态数据必须考虑随机测量噪声等引起的干扰。在数值仿真时，人工噪声应添加到模态数据中，这里采用Udwadia[16]提出的方法来模拟试验测量数据，并利用带噪声的模拟试验测量数据计算相应的模态应变能。为了获取相应的云模型数字特征，考虑了20次随机测量数据，由于加噪后结构可能会出现个别噪声敏感单元，对噪声敏感单元采用异常值过滤方法进行消减，消减系数为0.5。笔者主要采用了前3阶模态进行损伤识别研究，并考虑了3%的噪声水平。

图1 二维桁架结构Fig.1 Two-dimensional truss structure

3.1 算例1

单元6和单元23发生损伤，刚度降低25%和30%，为了进行对比，分别采用了模态应变能耗散率指标MSEDRI、模态应变能等效指标MSEEI和模态应变能均化指标MSEMI进行计算，计算结果如图2所示。从图2可以看出，3种指标均能进行损伤的定位识别，其中，MSEEI和MSEMI的定位效果要更好，而MSEDRI可能会对单元26产生误识别问题。为了进一步对损伤定量结果进行分析，3种应变能指标对于损伤单元的计算结果如表1所示。从表1可以看出，3种指标均具有一定的损伤定量能力，其中，笔者建议的模态应变能均化指标MSEMI的识别效果明显更好，故选取模态应变能均化指标MSEMI进行损伤识别研究。

图2 单元6、23损伤的3种指标的识别结果Fig.2 Identification results of three kinds of indexes when damages occur in the 6th and 23rd elements

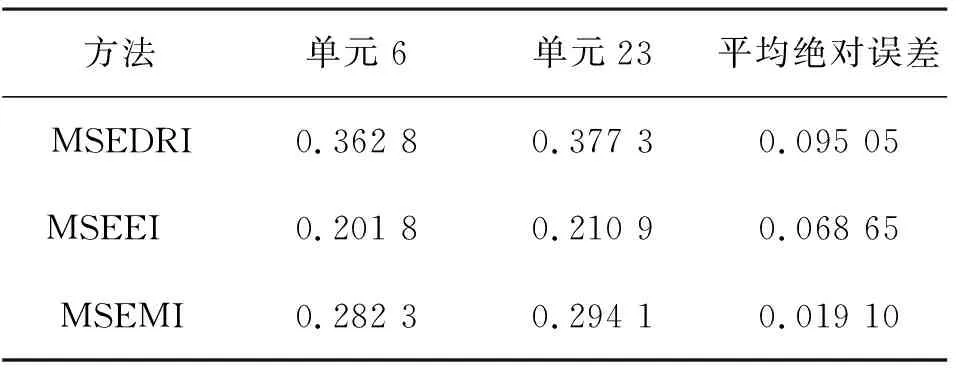
方法单元6单元23平均绝对误差MSEDRI0.362 80.377 30.095 05MSEEI 0.201 80.210 90.068 65MSEMI0.282 30.294 10.019 10

在实际应用中，测量噪声不可避免，故考虑位移模态有3%的测量噪声干扰时，采用20次含噪的随机测量数据，并利用模态应变能均化指标MSEMI和云模型相结合进行损伤识别研究。通过计算采样数据的云数字特征，得到期望的计算结果如图3所示。从图3中可以发现，利用期望值能进行损伤的定位识别，且定位的效果较好，能基本识别出损伤单元为单元6和23。同时计算出单元的确定度函数，损伤单元的确定度如图4所示。从图4可以看出，当损伤单元的确定度越高时，越接近于损伤的期望值，云滴的分布相对越集中。

图3 单元6、23损伤的MSEMI指标的期望识别结果(考虑3%的测量噪声)Fig.3 Expectation identification results of three kinds of indexes when damages occur in the 6th and 23rd elements(considering 3% noise)

图4 算例1损伤单元的确定度Fig.4 Certainty of damaged elements for case 1

3.2 算例2

单元3、16、21发生损伤，刚度降低25%、35%和30%，为了进行对比，同样采用了模态应变能耗散率指标MSEDRI、模态应变能等效指标MSEEI和模态应变能均化指标MSEMI进行计算，计算结果如图5所示。从图5可以看出，3种指标均能进行损伤的定位识别，其中MSEEI和MSEMI的定位效果依然要更好，而MSEDRI则可能会对单元1和2产生误识别问题。为了进一步对损伤定量结果进行分析，3种应变能指标对于损伤单元的计算结果如表2所示。从表2可以发现，3种指标均具有一定的损伤定量能力，其中，笔直建议的模态应变能均化指标MSEMI的识别效果明显更好。故模态应变能均化指标MSEMI仍可以作为有效的损伤识别指标。

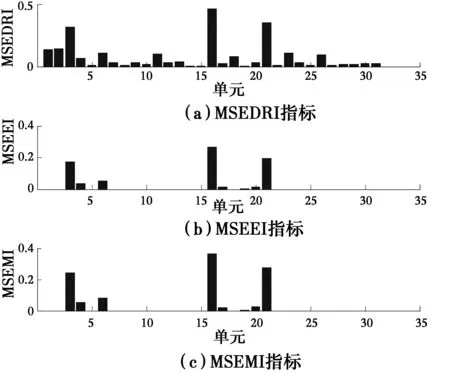
图5 单元3、16、21损伤的3种指标的识别结果Fig.5 Identification results of three kinds of indexes when damages occur in the 3rd, 16th and 21st elements

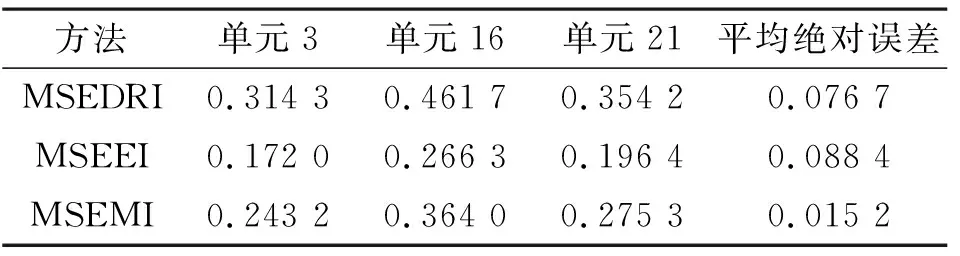
方法单元3单元16单元21平均绝对误差MSEDRI0.314 30.461 70.354 20.076 7MSEEI 0.172 00.266 30.196 40.088 4MSEMI0.243 20.364 00.275 30.015 2

当考虑测量噪声时，主要考虑位移模态有3%的测量噪声干扰，采用20次含噪的随机测量数据，并利用模态应变能均化指标MSEMI和云模型相结合进行损伤识别研究。通过计算采样数据的云数字特征，得到期望的计算结果如图6所示。从图6可以看出，利用期望值可以进行损伤的定位识别，且定位的效果较好，可以基本识别出损伤单元为单元3、16、21。同时计算出单元的确定度函数，损伤单元的确定度如图7所示。从图7可以看出，损伤单元的确定度越高时，越接近于损伤的期望值，云滴的分布也相对越集中。

图6 单元3、16、21损伤的MSEMI指标的期望识别结果(考虑3%的测量噪声)Fig.6 Expectation identification results of three kinds of indexes when damages occur in the 3rd,16th and 21st elements(considering 3% noise)

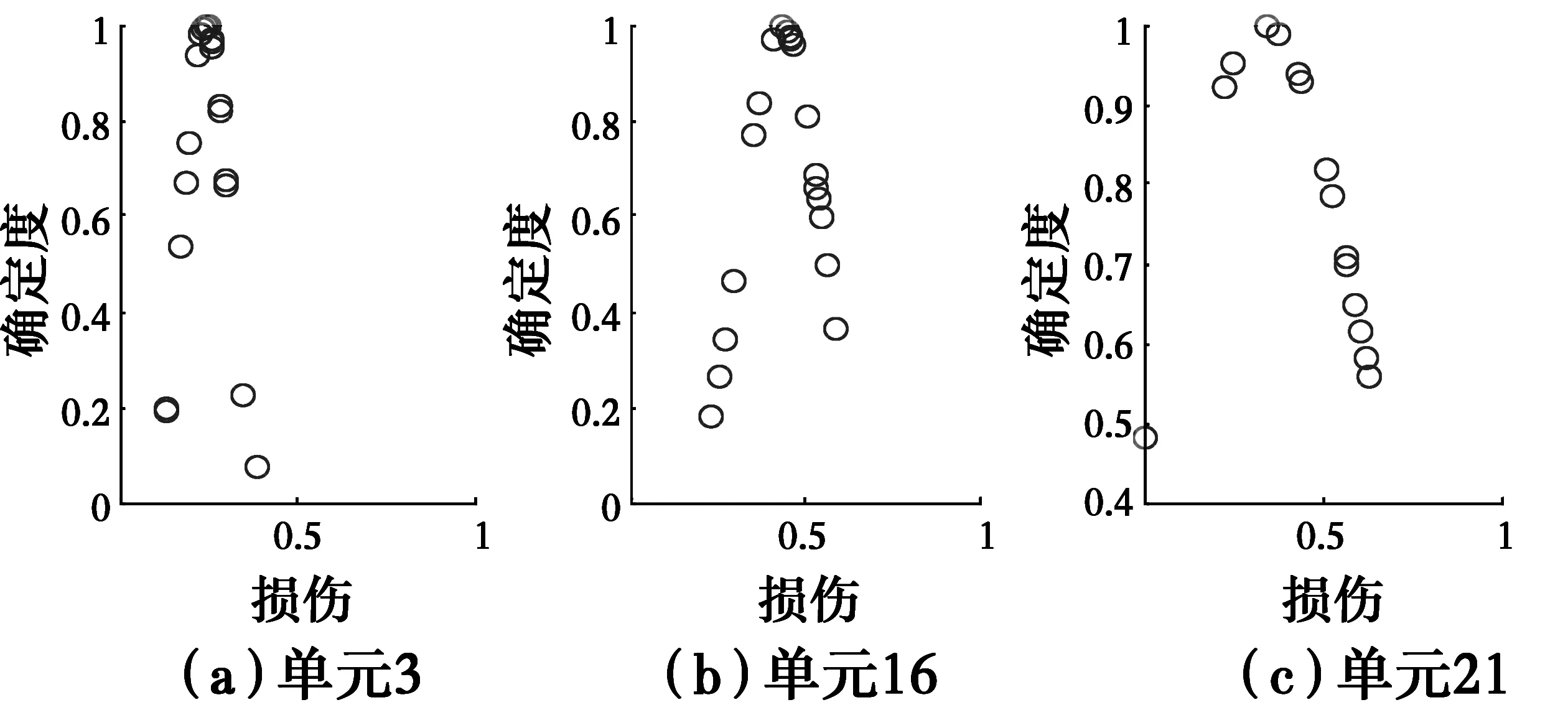
图7 算例2损伤单元的确定度分析Fig.7 Certainty analysis of damaged elements for case 2

由以上两个算例可以看出，3种模态应变能指标均能进行损伤的定位和定量研究，而且模态应变能均化指标MSEMI的定位和定量效果更好，故选取该模态应变能均化指标和云模型相结合来处理测量噪声引起的不确定性问题。通过计算出的云模型期望值，依然可以进行损伤的定位识别，通过确定度分析也可发现云模型的期望值具有对含噪数据进行损伤识别的能力。

4 结论

提出了模态应变能均化指标，以及模态应变能和云模型相结合的损伤识别方法。通过对已有的模态应变能指标进行分析，建立了一种模态应变能均化指标，考虑了随机测量噪声等引起的不确定性问题，采用了云模型的数字特征和确定度方法来处理相应的不确定性问题。通过数值计算和理论分析，可以得到以下结论：

1)当不考虑测量噪声时，模态应变能耗散率指标、等效指标、均化指标均能较好地进行损伤的定位和定量识别，其中模态应变能均化指标的识别效果更好。

2)当考虑测量误差引起的不确定问题时，模态应变能均化指标和云模型相结合能较好地处理该类问题，通过多次测量数据，并利用期望值能对结构损伤进行识别，并能分析相应的确定度问题。由于现实的工程结构往往较为复杂，采用云模型技术对于大型复杂结构的损伤识别研究仍需进一步探索。

参考文献：

[1] LAM H F, YANG J H. Bayesian structural damage detection of steel towers using measured modal parameters [J]. Earthquakes & Structures, 2015, 8(4): 935-956.

[2] LI P J, XU D W, ZHANG J. Probability-based structural health monitoring through Markov chain Monte Carlo sampling [J]. International Journal of Structural Stability and Dynamics, 2016, 16 (7): 1550039-1-1550039-16.

[3] YUEN K V, AU S K, BECK J L. Two-stage structural health monitoring approach for phase I benchmark studies [J]. Journal of Engineering Mechanics, 2004, 130(1): 16-33.

[4] KOH B H, DYKE S J. Structural health monitoring for flexible bridge structures using correlation and sensitivity of modal data [J]. Computers & Structures, 2007, 85(3/4):117-130.

[5] MORASSI A, ROVERE N. Localizing a notch in a steel frame from frequency measurements [J]. Journal of Engineering Mechanics, 1997, 123(5):422-432.

[6] 刘济科, 杨秋伟. 基于残余力向量的结构损伤识别两步法[J]. 中山大学学报(自然科学版), 2004, 43(4): 1-4.

LIU J K, YANG Q W. A two-step method for structural damage identification based on residual force vector [J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2004, 43(4): 1-4. (in Chinese)

[7] SHI Z Y, LAW S S, ZHANG L M．Structural damage localization from modal strain energy change [J]. Journal of Sound and Vibration, 1998, 218(5): 825-844.

[8] SAZONOV E, KLINKHACHORN P. Optimal spatial sampling interval for damage detection by curvature or strain energy mode shapes [J]. Journal of Sound and Vibration, 2005, 285(4/5): 783-801.

[9] 刘晖，瞿伟廉，袁润章. 基于模态应变能耗散率理论的结构损伤识别方法[J]. 振动与冲击，2004，23(2): 118-121.

LIU H, QU W L, YUAN R Z. Structural damage detection method based on the theory of dissipationratio of modal strain energy [J]. Journal of Vibration and Shock, 2004, 23(2): 118-121. (in Chinese)

[10] GUO H Y, LI Z L. Structural damage identification based on Bayesian theory and improved immune genetic algorithm [J]. Expert Systems with Applications, 2012, 39: 6426-6434.

[11] 郭惠勇，盛懋. 基于模态应变能的不同损伤指标对比[J]. 河海大学学报(自然科学版), 2014, 42(5): 444-450.

GUO H Y, SHENG M. A comparative study of different modal strain energy damage indexes [J]. Journal of Hohai University (Natural Sciences), 2014, 42(5): 444-450. (in Chinese)

[12] HU H W, WU C B. Development of scanning damage index for the damage detection of plate structures using modal strain energy method [J]. Mechanical Systems and Signal Processing, 2009, 23(2): 274-287.

[13] SEYEDPOOR S M. A two stage method for structural damage detection using a modal strain energy based index and particle swarm optimization [J]. International Journal of Non-Linear Mechanics, 2012, 47(1):1-8.

[14] LI D Y. Uncertainty in knowledge representation [J]. Engineeringence, 2000, 2(10): 73-79.

[15] LI D Y, LIU C, GAN W. A new cognitive model: Cloud model [J]. International Journal of Intelligent Systems, 2009, 24 (3): 357-375.

[16] UDWADIA F E. Structural identification and damage detection from noisy modal data [J]. Journal of Aerospace Engineering, 2005, 18(3): 179-187.