基于自适应差分进化算法拟合圆的树干胸径测量方法

胡春华 李萍萍 金成磊 朱 乐

(1.南京林业大学信息科学技术学院， 南京 210037； 2.南京林业大学生物与环境学院， 南京 210037)

0 引言

林业生产中，森林资源调查与数据采集是一个重要环节。树木胸径是立木测定的最基本因子之一。测量树木胸径可以了解树木生长状况，为树木可视化以及整个林区的生产控制提供重要数据。早期测量胸径采用卡尺或围尺人工测量[1]，这种测量方式劳动强度大，特别是对于有杂草的森林。随着电子技术的不断发展，各种测量树干胸径方法相继产生，实现无接触的树干胸径测量[2-16]。有学者采用数字图像方法获取树干胸径，如利用条形码阅读器扫描并读取树干上带有树木胸径的条形码带的数值[2]，获得树干胸径。王雪峰等[3]采用原野服务器传回的图像，并通过立体的视觉技术重建了远距离树木的胸径。王建利等[4]采用光学三角形测量理论，搭建一个由线性激光传感器与CMOS图像传感器组成的测量系统，通过图像数据与树干坐标信息获取树干表面轮廓图像，最后通过最小二乘拟合椭圆法求取树干胸径。除了直接根据图像获取树干直径以外，FORSMAN等[5]采取多视觉图像重构树干，获得树干点云数据，采用Gauss-Newton法拟合圆，求取树干胸径。黄晓东等[6]采用CCD、倾角传感器、距离传感器等设计了一套自动测量胸径与树高的测量仪。近几年，较多学者采用地面激光点云数据分析树干参数[7-11]，也有较多学者采用二维激光数据测量树干直径[12-15]。也有学者融合激光传感器与机器视觉测量单木树胸径[16]。机器视觉比较符合人的思维，但是在自然环境下，容易受到光照等条件的影响。地面激光雷达技术点云数据处理非常费时，二维激光技术特别是胸径位置处采用二维激光技术测量速度较快，且轻便，容易制成测量仪。

在解决优化问题中，差分进化算法(Differential evolution, DE)是一种非常有效的优化算法[17]。它是由STORN等[18]于1995年提出的。为解决差分进化算法对参数敏感的问题，许多研究者提出了参数自适应的差分进化算法。QIN等[19]提出了自适应差分进化算法(SaDE)。LIU[20]提出参数自适应差分算法(JADE)优化JIT(Just-in-time)与相关向量机(Relevant vector machine，RVM)。PEUURI等[21]针对DE/rand/1/bin策略算子提出一种自适种群数的DE算法，找出合适的交叉概率与对应的种群数，变异尺度在[0,1)内随机取，该算法对较复杂的函数优化效果较好。本文提出一种新的非接触式测量树干胸径方法，采用实验室自制的基于激光传感器的履带移动机器人胸径测量平台测量树干胸径。针对树干近似圆形，将传感器采集的树干表面参数用圆进行拟合，拟合出圆的半径，从而获得树干胸径。针对本研究数据，在PEUURI等[21]研究基础上，加入自适应策略与自适应控制参数，实现圆的参数拟合。

1 实验材料

本文实验数据采用实验室自制胸径测量仪测量获得，其测量平台示意图如图1所示，以Arduino为微处理器设计测量控制系统。采用长、宽、高为540、280、110 mm 的履带小车为载体，将控制器以及传感器固定在智能小车平台上。平台上固定一伸缩式铝合金撑杆，底部用螺丝螺母连接于小车底盘上，高度可以调整。撑杆顶端带有三维多角度旋转云台，可以满足多角度的测量需求。激光传感器(VL53L0X型)与舵机用L型连接件连接，采用透明亚克力塑料板作为激光传感器的固定板，用螺丝固定在L型金属连接件上。测量平台采用红外接收模块与红外遥控器控制小车前进、后退、左右转、停止以及采集数据等。测量数据存放于控制系统的SD卡内。采用超声波传感器测量树干表面到测量平台的距离。

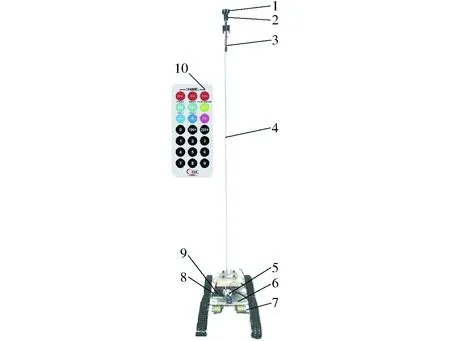
图1 测量平台示意图Fig.1 Sketch of sample collection platform1.激光传感器 2.舵机 3.控制线 4.可调整铝合金撑杆 5.超声波传感器 6.履带移动机器人平台 7.电动机 8.控制系统 9.红外接收模块 10.红外遥控器

测量平台可以通过遥控器实现远程控制，控制测量平台运动与数据采集。激光传感器测量范围在2 m以内。本实验平台测量范围为50～1 000 mm，测量精度为±1.0 mm，舵机转角范围在0°～180°，环境工作温度为-10～45℃。

2 自适应差分进化算法拟合圆

2.1 拟合圆方程的建立

由于大部分树干呈圆台形，对于同一高度的树干截面呈圆形，故根据同一平面上任意3个点能确定圆。为了使拟合圆更精确，每次舵机带动激光传感器从0°到180°采集数据，对同一个方位采集3次。如图2所示，每次采集数据时传感器自动调整到零初始位置。初始位置设置为极坐标起始坐标位置，传感器中心为坐标原点，每隔15 ms激光传感器转动1°，采集一次数据,数据单位均为mm。将采集到的数据利用K-means算法聚类，保留目标数据点。如图2所示，设转动角度与初始位置之间的夹角为α。设拟合圆心坐标为(xc,yc)，半径为R，采集样本点t时刻的坐标(xt,yt)到圆心距离为dt，其中xt=ρtcosα，yt=ρtsinα，ρt为传感器到树干表面的距离，为使样本点尽可能拟合在圆心为(xc,yc)、半径为R的圆上，则所有样本点到圆心距离与半径差的和应最小，即优化目标方程为

(1)

(2)

(3)

式中N——目标样本点数θ——优化参数

图2 样本采集原理示意图Fig.2 Sample collection principal diagram

圆心坐标与半径均为未知数，即优化参数θ=(xc,yc,R)。需要拟合优化算法对其进行优化，基于梯度的Levenberg-Marquardt(LM)优化算法、进化优化算法、粒子群优化算法等均有各自的优缺点。本文采用差分进化算法拟合圆。

2.2 自适应差分进化算法

差分进化算法是基于群体智能理论的优化算法，通过群体内个体间的合作与竞争产生的群体智能指导优化搜索，主要有变异、交叉与选择3个过程，而算法过程中的种群初始化、种群规模、进化策略、变异尺度以及交叉概率等均影响优化算法的收敛性与鲁棒性。因此本文主要对种群规模、进化策略、进化算子以及交叉概率在进化过程中自适应调整进行研究，其算法过程如下：

(1)初始化

设置初始化种群与代数以及计算过程中的其他参数初始值。假设用G=0,1,…,Gmax表示进化代数，则当前代数下种群中第i个个体表示为

Xi,G=(xi,G,1,xi,G,2,…,xi,G,D)
(i=1,2,…,Np)

(4)

式中D——种群个体维数

Np——种群个数

在种群初始化时,初始的种群需覆盖整个搜索空间RD，初始化为

xi,0,j=xL,j+r(xU,j-xL,j)
(j=1,2,…,D)

(5)

式中xU,j——第j维的上界

xL,j——第j维的下界

r——[0,1]区间内均匀分布的随机数

种群个数必须大于进化向量数，目前较多的学者对种群个数Np进行研究，种群个数与种群向量幅度有关，本研究采用PEUURI等[21]提出的种群自适应算法

Np=kDln(xU-xL+e)

(6)

式中k——比例系数

xL——下界xU——上界

本文D为3，初始种群数Np0=30，k由PEUURI 等[21]提出的自适应算法获取。

(2)差分变异操作

在当前代数中，对于每一个个体矢量Xi,G(称为目标矢量)，使用变异算子生成一个新的个体Vi,G(称为变异矢量)。目前变异策略有多种形式，经过多次实验可知DE/rand/1/bin策略与DE/current-to-best/1策略对圆拟合效果较好，从当前种群中随机挑选3个个体矢量Xr1,G、Xr2,G与Xr3,G，并选出最优Xbest,G，则变异策略为[22]

(7)

(8)

式中Fi——变异尺度因子

ζ——选择概率

λ——自适应因子，取0.5

γ——常数，取0.01

对差分矢量进行缩放，从而控制搜索步长。较大Fi对全局搜索比较有效，较小的Fi可以加速收敛。可见，选择合适的Fi非常重要，一般选择Fi∈(0.4，0.9)，然而对不同的进化代数Fi不是一个定值，Fi随着进化过程变化而动态变化。本文选用文献[23]提出的按照Cauchy分布，其参数随进化代数变化而变化。

(3)交叉操作

差分进化算法采用离散交叉算子:二项式交叉和指数交叉。交叉算子把通过变异操作得到的变异矢量Vi,G与个体目标矢量Xi,G进行离散交叉生成试验矢量Ui,G，具体的二项式交叉操作为

(9)

式中Cri——第i次进化交叉概率因子

jrand——随机整数

一般Cri∈(0，1)，但在Cri∈(0.1，0.8)时更有效。在j维上，若随机生成数小于Cri时，试验矢量继承变异矢量，反之继承父代目标矢量。一般而言Cri越大则选择的交叉位也就越多，意味着试验矢量更倾向于变异矢量。本文Cri随着进化过程正态分布，其正态分布均值随进化代数变化而变化[23]。

(4)选择操作

差分进化算法通过变异操作和交叉操作产生后代群体之后，采用一对一的贪婪筛选算子将子个体与相应的父个体进行比较，较优者保存到下一代，选择操作为

(10)

(5)优化结束条件判断

若不满足最大迭代次数1 000，继续进化过程，采用式(6)更新种群数，进入变异、交叉与选择过程。否则结束进化优化过程，输出最优值。

3 实验与分析

图3 样本采集场景Fig.3 Sample collection scene

在林分测定中，胸径(DBH)指树干距离地面以上1.3 m处树干的直径。本次测量平台为履带机器人平台，样本采集场景如图3所示。为验证机器人行走稳定性，在校园与人工林地随机选择大小不同的40棵树进行测量，对每一棵树进行标记。为验证本文测量系统测量胸径的准确性，首先对标记好的树采用围尺人工测量出胸径值作为树干胸径实际值，其数据统计分析表如表1所示。

表1 样本胸径统计Tab.1 DBH statistics of measured sample mm

为验证系统测量的稳定性，分别在阴天的早晨、中午、下午与晴天的早晨、中午、下午进行了6次数据测量，每次对每个场景(校园与人工林地)有标记的40棵树以相同顺序进行测量记录数据，每次测量3个方位，求取平均值作为测量值。实验数据处理器为Intel i5-6500 CPU 3.2 GHz，内存8.0 GB，数据处理软件为Matlab 2016b。

激光传感器采集的数据由树干表面反射到传感器的时间与速度计算出来，由于激光传感器存在一定的发散性，本研究首先将采集的数据经过发散角校正，然后计算树干表面点的坐标值。分别将不同时间段与不同方位采集的数据采用K-means算法分割出目标数据。采用文献[14]提出的弧长法矫正激光传感器的发散角，拟合出发散角二次方程，每次计算时采用角度补偿的方式减少误差，拟合R2为0.907，均方根误差(RMSE)为0.626°,其方程为

Fρ=-0.000 592ρ2+0.064 28ρ-11.1

(11)

式中ρ——激光传感器中心到树干表面点距离，mm

Fρ——补偿角，(°)

补偿角随着距离的增加而增大，因此每次计算树干表面点坐标值之前，将对应的角度减去补偿角即为补偿后角度。

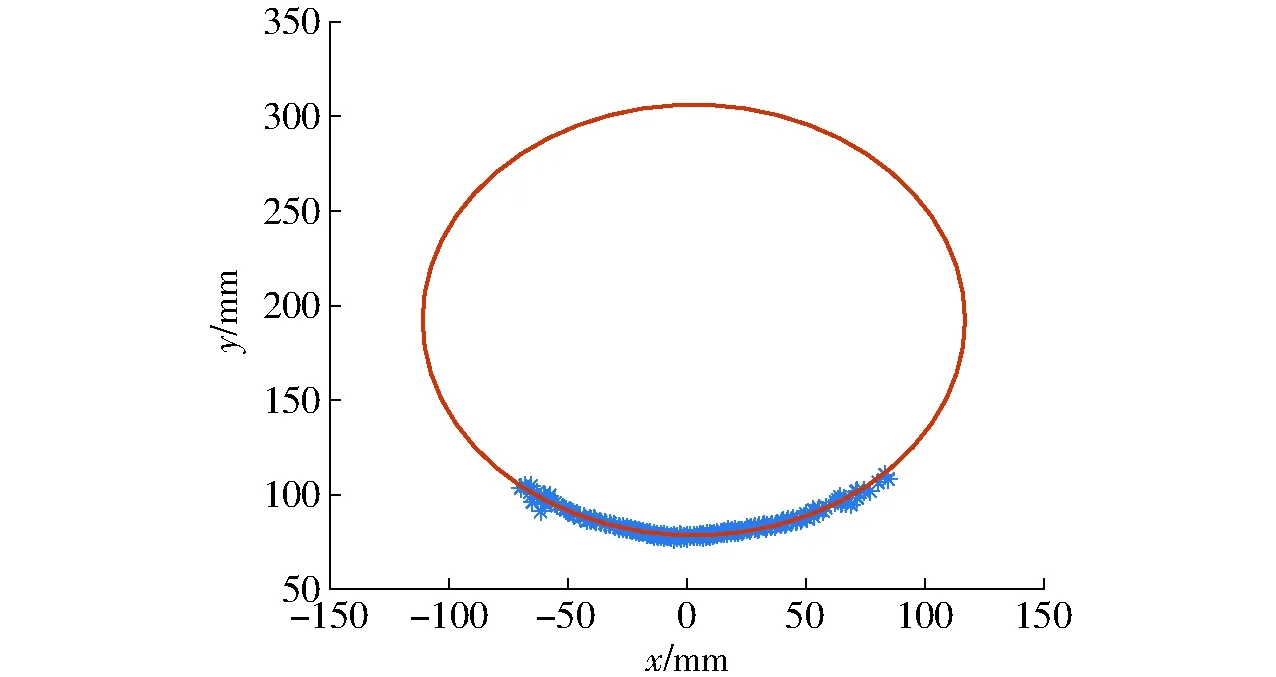
图4 二维坐标点拟合圆Fig.4 Two dimensional coordinate point fitting circle

计算出补偿后数据对应的坐标值，采用2.2节的自适应差分进化算法拟合圆。图4是经过处理后的数据点拟合圆效果图，显示大部分数据点比较集中在圆弧上，极少部分数据有一定的偏差，由于树干表面不是绝对的光滑，因此表面的部分数据不在同一圆弧上。但是对于同一个方向的数据点，大部分在同一个圆弧上。分别对3个方向的数据进行分割与拟合，拟合出最优半径，计算3个方向的平均值即为本文所求树干胸径。

本次实验分别对基于梯度下降法Levenberg-Marquardt(LM)优化算法、非梯度算法粒子群方法(PSO)以及本文提出的自适应差分进化算法(ADE)进行了比较分析。对同一组数据进行比较，其结果如表2所示，基于梯度下降方法的LM算法收敛较慢，运行时间较长，PSO算法与ADE算法收敛速度快，而ADE算法最快。拟合圆的直径较相近，因此均方根误差RMSE相差较小。从实验结果可以看出，ADE算法较优。

表2 不同算法拟合结果比较Tab.2 Comparison of different algorithms

将Hough变换算法与ADE算法进行比较。对同一棵树的6次测量数据进行了统计分析，测量误差在±5 mm之间，求取平均值作为测量值。将实验测量值分别与实际值进行对比分析，图5与图6分别给出了校园内与人工林地不同直径的40棵树胸径测量值与实际值之间的关系。由图5与图6可知，本文算法数据点较集中。表3给出了采用本文算法与Hough变换算法拟合的测量值与实际值的直线拟合结果。本文算法对校园内数据拟合直线斜率为0.993，偏离值为3.782，R2为0.989，RMSE为4.996 mm。而Hough变换算法拟合的直线斜率为1.038，偏离值为-7.981，R2为0.947，RMSE为12.18 mm。对于人工林地，本文拟合算法的RMSE为4.500 mm，Hough变换算法的RMSE为11.97 mm。由实验分析可知，本文测量胸径方法受样地场景影响较小。虽然本文算法拟合圆效果较好，但是实际值与测量值之间存在一定的误差。引起误差的因素较多，如树干实际测量的误差、传感器误差以及传感器发散角补偿误差等。在以后的研究工作中，应尽量减少测量误差，提出更有效的发散角补偿算法，使测量值更逼近于真实值。

4 结论

(1)采用实验室自制的基于激光传感器的胸径测量平台对校园内与人工林地不同直径的40棵树进行多次测量，每次测量对同一棵树采集3个方向的数据，每个方向采集3次，获得不同方位的测量数据，并将数据保存于SD卡。

(2)对采集的数据采用K-means进行聚类，分

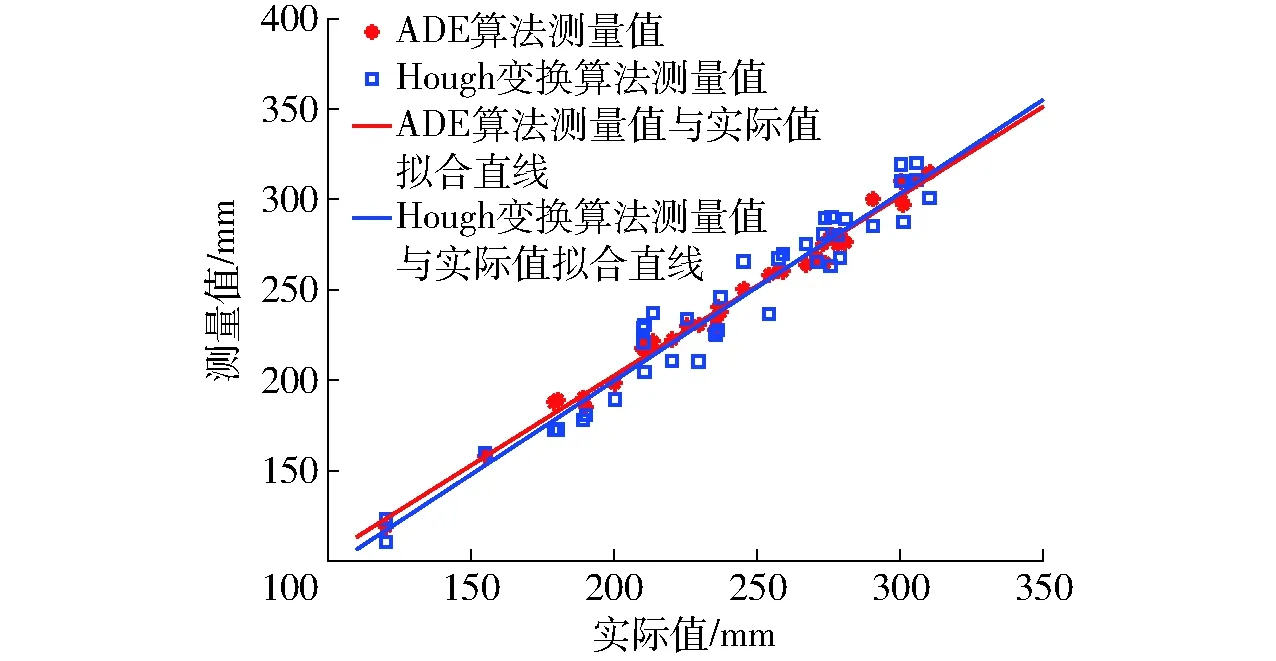
图5 校园内树干胸径测量值与实际值关系Fig.5 Relationship between actual DBH and measured DBH in campus

图6 人工林地树干胸径测量值与实际值关系Fig.6 Relationship between actual DBH and measured DBH in artificial forest

拟合方法拟合方程RMSE/mmR2ADE算法校园内y=0.993x+3.7824.9960.989人工林地y=0.979x+4.9754.5000.993Hough变换算法校园内y=1.038x-7.98112.180.947人工林地y=0.973x+8.51211.970.955

割出背景与目标。采用弧长法计算出补偿角与激光传感器到树干表面点距离的拟合公式。将采集到的数据角度分别减去补偿角度，对分割的目标样本数据进行补偿。对补偿后的数据，以激光传感器中心为坐标原点，计算出树干表面点的横纵坐标。

(3)根据每棵树的横纵坐标，分别采用基于梯度的LM优化算法、粒子群(PSO)优化算法、本文提出的自适应差分进化算法以及Hough变换算法拟合圆测量出树干胸径，并对测量值与实际值进行了分析与比较。本文算法拟合时间最短，为1.41 s，对校园内和人工林测量结果与实际值比较分析，RMSE分别为4.996 mm与4.500 mm。实验结果表明，本文提出的自适应差分进化算法收敛快，且比Hough变换拟合圆方法更逼近真实值。