多光谱影像混合像元解混的加权变异系数分析法

宇 洁 叶 勤 林 怡

(1.同济大学测绘与地理信息学院, 上海 200092; 2.同济大学环境科学与工程学院, 上海 200092)

0 引言

混合像元普遍存在于中低分辨率的遥感影像中，给图像定量化解译造成困扰[1]。因此，如何准确获取组成混合像元的端元类型及其在像元中的丰度值成为定量遥感的研究热点[2]。混合像元丰度值解算精度的高低很大程度上取决于端元信息获取的准确性[3]。目前，针对混合像元端元提取和选择问题，国内外学者展开了大量研究。

常见获取端元信息的方法可分为：利用地物光谱仪实地采集光谱数据[4-5]、从典型地物光谱库中获取[6-7]和直接在影像上选取[8-9]。前两种方法多适用于高光谱数据，而针对多光谱数据时，现有的研究多采用直接从数据本身获取的方法。在大多数传统混合像元端元提取和选取算法中，假设不同端元的光谱特征具有类别间差异性和时空稳定性，即不同地物具有绝对不同的光谱特征曲线和同类地物的光谱曲线不会受外在因素的影响而变化。然而，受到传感器、大气、周围环境等因素的影响，影像上普遍存在同物异谱和同谱异物的现象[10]。同时对于状态会随时间发生变化的地物，同一遥感数据中可能包含同类地物多种状态的不同光谱特征(如同种植被不同生长状态)。当影像中存在上述端元差异问题时，将极大影响影像中典型端元提取的准确性和混合像元分解的精度。此时，传统端元提取与选择的方法将不再适用。目前国外学者对端元问题已经展开了许多研究，而在国内，对此问题的研究尚不多。本文将针对中低分辨率多光谱遥感影像上端元差异问题展开深入研究。

1 常用算法分析

端元差异问题主要包含端元类内差异(Intra-class variability)和类间差异(Inter-class variability)[11]。各类算法通过在一定程度上缩小类内差异、扩大类间差异来达到提高解混精度的目的。SOMERS等[12]将现有的解决端元差异的算法分成5大类：迭代混合分析、光谱特征选择、光谱波段加权、光谱转换和光谱建模。

(1)迭代混合分析类算法首先需要定义由所有可能端元组合组成的端元组合候选库。然后针对每个混合像元，通过循环迭代的方法从候选的端元组合库中选出适合该像元的最优端元组合作为该像元的解混结果。多端元光谱混合分析(Multiple endmember spectral mixture analysis, MESMA)[13]是其中应用最为广泛的一种算法[14-16]。虽然此类算法能够有效地解决端元类内差异问题，但也大大增加了算法的计算量。同时此类算法在波段较少的多光谱数据中的应用也存在局限性。

(2)光谱特征选择则是选取某个特定指数作为评定指标，对各个波段的指标值进行排序后选择能使类内差异最小和类间差异最大的光谱特征组合。常用算法包括主成分分析(Principle component analysis, PCA)[17]、最佳指数因子(Optimal index factor, OIF)[18]、互信息(Mutual information, MI)[19]、不稳定指数(Instability index, ISI)[20]等。此类算法虽然能有效避免计算量过大的问题，但在波段筛选过程中会有部分信息丢失。

(3)光谱波段加权是在传统各波段等权参与解混的基础上，对与类内端元差异相关性较小、与类间端元差异相关性大的波段赋予更高的权重。此类算法虽在一定程度上减小端元差异带来的影响[21-22]，但目前权重设置没有统一理论模型，常常需要根据研究区域实际情况和专家知识来确定。

(4)光谱转换是将原始波段数据经过一系列小波变换[23]、求导[24]、归一化变换[25]等，获得具有更小类内差异和更大类间差异的新特征值来进行混合像元解混。转换过程虽然降低了数据冗余度，但数据容易受到噪声及其它不确定因素污染，影响最终解混结果准确性。

(5)光谱建模算法则建立在各种辐射传输模型理论基础上，根据研究区域具体环境、气候因素，构建相应的地物波谱库。但模型的准确构建需要一定的先验知识。

5类算法中，光谱特征选择算法因为计算简单、易于实现的优点而被广泛用于解决端元差异问题。本文针对普遍存在的端元差异问题，为了避免端元因在不同波段的光谱值的数值尺度相差很大带来的影响，将变异系数(Coefficient of variation, CV)[26]的概念引入光谱波段选择研究中。结合特征选择类和加权类算法的优点，基于不等权思路提出一种能够自动定权的加权变异系数分析法(Weighted CV analysis, WCVA)，尽可能减小端元差异问题带来的影响。并从理论基础和真实数据验证两方面论证WCVA在解决端元差异问题中的可行性。以多光谱影像(TM影像)作为实验数据，采用对应更高空间分辨率的多光谱影像(Geoeye影像)作为参考丰度值进行定量精度评定。将WCVA的结果与常用的OIF方法的结果进行比较，并验证其优越性。

2 算法原理

遥感数据最佳波段组合的定量分析原理是根据所包含的信息量最大或类间可分性最大的原则，选择最佳的波段组合，更利于影像解译。目前应用比较广泛的选取方法有最佳指数因子法(OIF)、波段熵比较法、协方差矩阵特征值法等。为了验证本文提出的WCVA算法的可行性，实验中同时设计了定量和定性两个对比实验，将WCVA结果与OIF结果做比较。

2.1 最佳指数因子(OIF)

在解决端元差异问题的光谱特征选择类别方法中，OIF[27]同时兼顾了单个波段影像的信息量和波段间的相关性，且计算简单、易于实现。因此，采用OIF结果与本文提出的算法进行对比。OIF计算公式为

(1)

式中σi——第i波段对应的标准差

rij——波段i和波段j间的相关系数

OIF指数越大，则相应波段组合包含的信息量就越大。

2.2 加权变异系数分析法(WCVA)

为了消除端元差异问题，需要尽可能减小类内端元间离散度和扩大类间端元的离散度。通过地物光谱曲线分析，发现研究区域内不同端元在不同波段的光谱数值尺度相差很大，此时单纯仅用标准差已经不能准确描述数据的离散程度。为了消除测量尺度的影响，研究中引入了CV的概念。

在概率论和统计学中，CV常常被用于描述数据分布的离散程度[28]。它是由标准差和均值的比值构成，表达式为

Cv=σ/μ×100%

(2)

其中

μ=∑xi/n

(3)

(4)

式中，σ和μ分别表示数据集X={x1,x2,…,xn}的标准差和均值。

CV能够有效消除测量尺度和量纲的影响，并已广泛应用于物理学、分析化学、工程学等领域。CV值越大，数据集的离散程度越大。

同时，因为不同波段对于端元差异问题的敏感程度不同，将对不同波段按照重要性差异设置不同的权值

(5)

其中

∑wi=1

(6)

式中Cvi——第i波段对应的CV值

基于以上公式，为了尽可能减小端元差异问题的影响，最小化端元类内差异、最大化端元类间差异，提出一种新的基于CV的加权波段选取策略(WCVA)：

(1)计算所有类间和类内候选端元在各光谱波段对应CV值。

(2)根据所得各波段CV值按照类间和类内分别进行重要性从高到低排序。

(3)选取类间CV值大且类内CV值小的波段组成新的波段组合。

(4)根据类间端元CV值计算新波段组合中各波段的权值，完成WCVA。

3 实验数据及流程

3.1 实验区域

选用空间分辨率为30 m的TM数据(获取时间为2009年8月28日)作为待分析图像，研究区域位于广西壮族自治区合浦县东部北海市沙田半岛，该半岛属于南亚热带季风型海洋性气候，主要由3类地物组成：水域、桉树林和裸地，如图1a所示。而研究区域内的桉树林由于砍伐原因处于不同生长阶段(图中已标出，S1、S2、S3为对应3个生长状态)，导致在光谱上也存在差异，即桉树林存在类内差异。同时，选用空间分辨率为2 m的GeoEye影像(获取时间为2009年10月16日)作为分解结果精度评定的参考影像。TM每个像素在GeoEye中对应15×15个像素。实验中TM和GeoEye数据均使用FLAASH模型进行预处理。

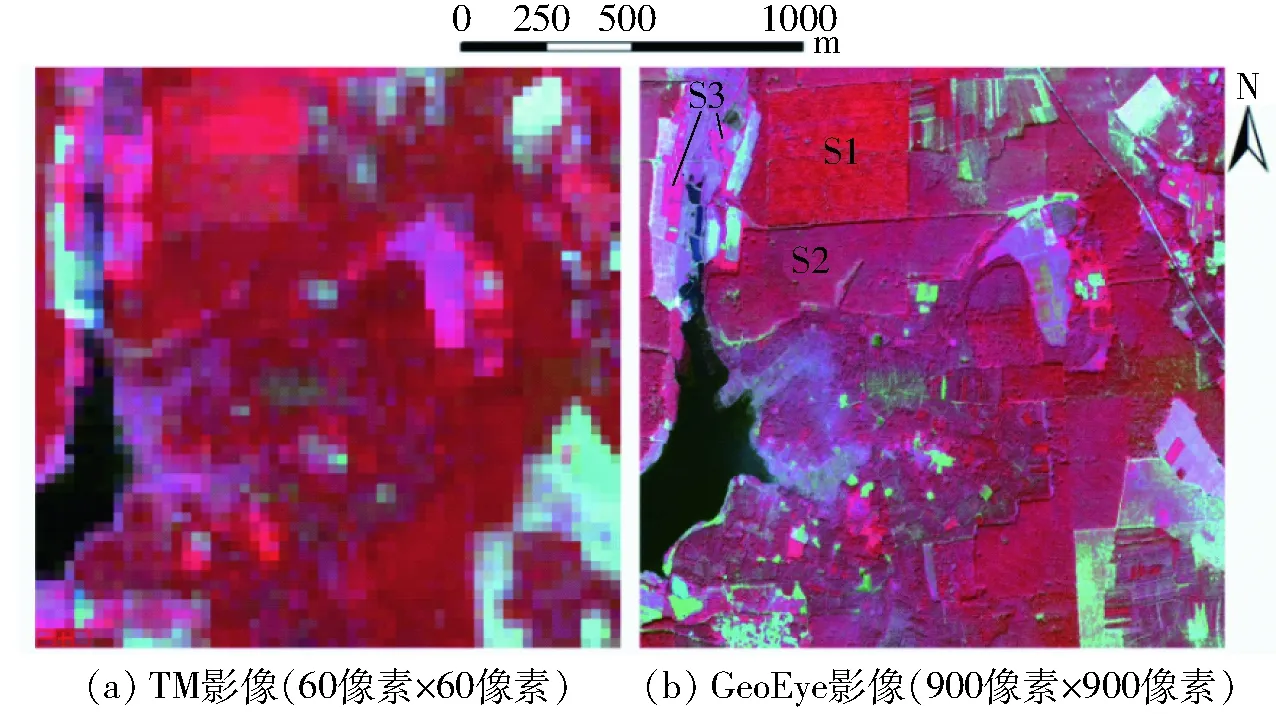
图1 研究区域多光谱假彩图像Fig.1 Multispectral false colour images

实验中的解混参考图由GeoEye影像处理后得到，设定原始GeoEye影像中所有像元均为纯像元。首先使用SVM将GeoEye影像分成3类(水域、桉树林和裸地)；然后用一个15×15的窗口进行逐行移动，统计窗口中各类地物的像元数；根据统计结果计算各类地物在15×15的窗口中所占百分比；最后按照百分比绘制丰度值参考图。

3.2 对比实验

图2是WCVA算法与对比实验整体流程图。实验将WCVA结果与OIF结果进行比较，并从定性对比、定量效率和精度3方面对WCVA进行精度评定:

(1)对所有可能的候选波段组合(考虑到研究区域内端元数量和解混算法的限制，本文候选波段组合由原始6个波段和所有可能的5个波段构成)进行主成分分析，以第一、二主成分作为横、纵坐标轴绘制样本点二维空间分布，根据不同类内及类间样本点分布情况对WCVA结果与OIF结果进行定性比较分析。

(2)统计OIF和WCVA运算时间，定量比较两种方法的效率。

(3)分别用多项式后非线性混合模型(Polynomial post-nonlinear model, PPNM)和模糊C均值(Fuzzy c-mean, FCM)模型对所有可能的候选波段组合进行混合像元解混。使用均方根误差(Root mean square error, RMSE)对各候选波段组合进行精度评定，定量比较分析WCVA与OIF的结果。

图2 WCVA算法与对比实验整体流程图Fig.2 Flow chart of WCVA approach

4 实验结果与分析

表1给出了不同波段对应水域、桉树林和裸地3类地物间和桉树林3个不同生长状态内的CV和OIF值，其中Bi表示第i波段。为了使类内(3个不同生长状态)差异最小、类间(水域、桉树林和裸地)差异最大，应尽可能选取类间高CV/OIF值、类内低CV/OIF值波段组成最优波段组合。

表1 各波段对应类内、类间端元差异的CV和OIF结果Tab.1 CV and OIF results of intra- and inter-class variability for different band combinations

根据最优波段选取准则将类内和类间各光谱的重要性按从高到低的顺序进行排序，结果见表2。通过分析可以发现，在CV结果中波段4的类内CV值高而类间CV值低，不利于减小端元差异，应当删除，故最优波段由波段1～3、波段5和波段7组成。而在OIF结果中，波段7或5更不利于减小端元差异，从而得出最优波段组合为：波段1～5，或者波段1～4+7两种组合。

表2 WCVA和OIF结果中各波段对应于类内差异和类间差异问题重要性排序Tab.2 Optimal band order of WCVA and OIF for intra- and inter-class variability

为了更直观比较各个波段组合结果，图3给出了所有可能的波段组合经PCA处理后各类间及类内端元的二维可视化分布图，并在图中标识出了桉树林类内的3个生长状态分布疏密情况。分布图分别以PCA变换后的第一和第二主成分作为横、纵坐标。很显然，CV结果给出的最优波段组合的类内端元分布更紧密，离散度更小，说明它在减小类内差异问题上更具有优势。同时，为了扩大类间差异，WCVA中各波段按照类间CV值结果进行波段加权，然后利用PPNM和FCM对加权后的各波段组合进行混合像元解混并计算解混结果的RMSE值(表3)。从表3可以看出，PPNM和FCM均在B1+B2+B3+B5+B7组合处获得最高解混精度，与WCVA结果一致。WCVA运算时间为0.942 s,明显比OIF的1.859 s短，其运算效率是OIF的2倍左右。

因此，WCVA与传统OIF方法相比，能够更快速、有效地减小类内差异问题并相对扩大类间差异，提高了最终的混合像元解混精度。

图3 各波段组合PCA变换后端元分布可视化图Fig.3 Visualization diagrams of different band combinations based on PCA

解混方法波段组合B2+B3+B4+B5+B7B1+B3+B4+B5+B7B1+B2+B4+B5+B7B1+B2+B3+B5+B7B1+B2+B3+B4+B7B1+B2+B3+B4+B5B1+B2+B3+B4+B5+B7PPNM0.2140.2140.2180.1830.2180.2190.213FCM0.1630.1630.1640.1600.1670.1670.162

5 结束语

端元差异问题普遍存在于中低分辨率的多光谱影像中，大大降低了端元提取的准确性和混合像元分解精度。为了减小端元差异问题对地物信息提取精度的影响，本文从特征选择及设置不同特征权重两方面出发，提出一种能自动定权的加权变异系数法(WCVA)。在WCVA中首先引入变异系数(CV)，避免了测量尺度和量纲的影响。然后，结合加权理论，以CV作为度量各波段对端元差异问题敏感程度的指标进行自动定权，提高了定权过程的自动化程度。最后根据最小化端元类内差异和最大化端元类间差异的原则构建解决端元差异问题的最优波段组合。同时，为了验证WCVA的可行性与有效性，选取OIF作为对比算法，设计了精度和效率两方面的对比实验。实验结果表明：通过 WCVA获得的最优波段组合在PPNM和FCM模型中的解混精度均明显高于OIF，而耗时仅为OIF的一半。因此WCVA在处理多光谱影像端元差异问题时具有精度高、计算量小的优势。