基于间接平差多项式拟合的周跳检测

张晟歌，程乃平，倪淑燕



基于间接平差多项式拟合的周跳检测

张晟歌，程乃平，倪淑燕

（航天工程大学 光电装备系，北京 101400）

在载波相位观测过程中，周跳的产生严重影响载波相位观测方式测量整周模糊度解算结果的准确度，所以在进行载波相位测量整周模糊度解算时，必须要在获得载波相位测量结果之前消除周跳。本文提出了一种有效探测周跳的算法。这个算法利用了基于间接平差的多项式拟合方法来载波相位接收过程进行拟合，这种算法在载波相位数据较少的情况下相较于一般的拟合方式有更快的速度，在数据较多时也有很好的解算稳定度,有效的改进了周跳的影响。

载波相位观测；周跳；间接平差；多项式拟合

0 引言

现阶段，卫星系统在导航、定位、测绘、控制等方面有着较为广阔的应用。卫星系统的定位方式主要分为伪距定位方式和载波相位定位[1]方式。在一些高精度的测量中，伪距定位方法的测量精度还不能满足要求。所以需要使用载波相位定位技术。整周模糊度的解算[2]问题是载波相位定位技术的一个研究重点。由于卫星的定位是一个动态的过程，载波相位实际的观测值不仅仅包含第一次测量获得的整周数以及接收机测量值。在测量的过程中，需要接收机对卫星发送的信号进行持续的跟踪。如果在跟踪的过程中出现了问题。接收机对卫星发送信号的跟踪过程发生中断的话载波相位的观测值就会发生周期性的跳变。这就会导致在利用载波相位定位结果进行模糊度解算时，获得的结果中带有整周的跳变。从而影响整周模糊度的解算的准确度。这对于后续的姿态解算有着很大的影响。为了解决这个问题，就需要对载波相位测量结果中出现的周期调变进行检测，并通过一定的方式进行修复。

理论上，如果周跳数较大时，可以通过直接观察的方式来发现周跳发生的位置。但是，一般而言，对于载波相位观测模型来说，由于星站之间的距离很大，而一般产生周跳时接收机的出现错误的时间并不长。所以，载波相位整周模糊度数远远大于整周跳变[3]，此时的差值相对于模糊度数过小，直接观测的方法就不适应这个场合。就需要用代数的方法来进行分析和求解。

本文分析了其中多项式拟合法进行周跳探测的方法，并提出了一种基于间接平差的探测算法，通过设置仿真对比多种算法的探测效率。

周跳问题，现在的方法（几种方法的比较），我要怎么做。

1 多项式拟合周跳检测

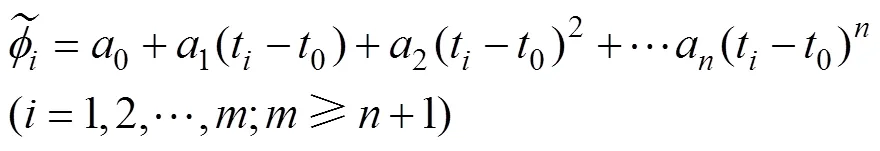
对于多项式拟合法[6-7]由于其与高次差法本质是相同的，在高次差法中，卫地距对于时间的四阶导数和五阶导数一般趋近于0，无法再用多项式来进行拟合、故多项式拟合的阶数一般不大于4阶即可。

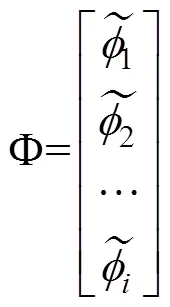
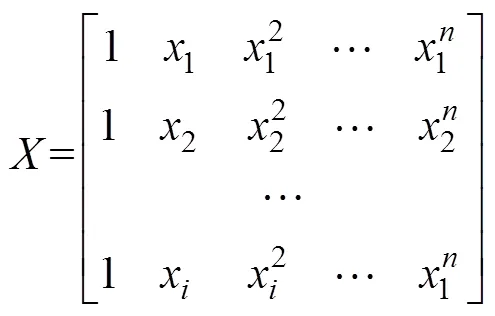
式（5）的矩阵表达形式为：

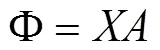
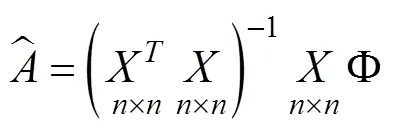
2 基于间接平差的多项式拟合周跳检测

2.1 间接平差法原理

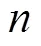
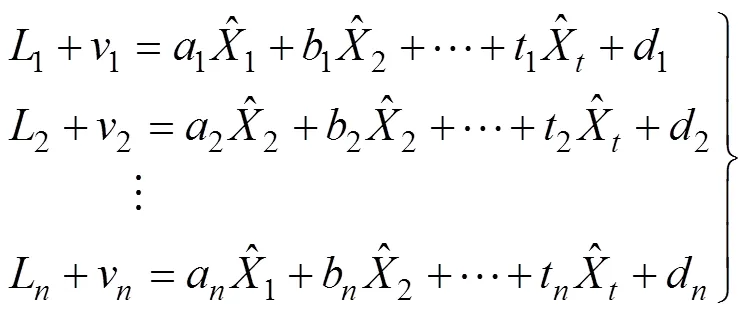
得到误差方程的一般形式为:

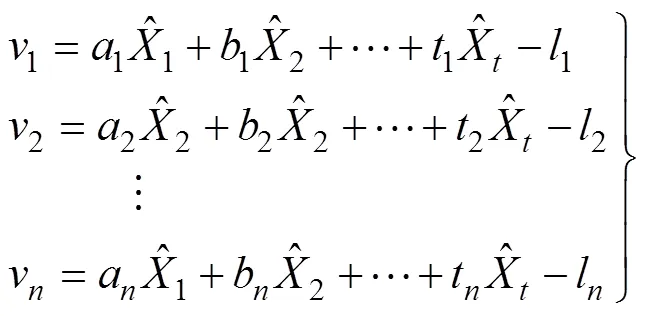
则可得误差方程的矩阵形式：

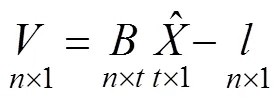
通过最小二乘方法可以求得最终估计量：

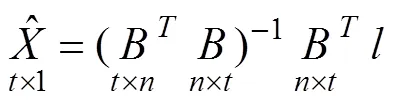
间接平差法[10-12]进行最小二乘计算时所需要的系数矩阵的维度，相较于一般最小二乘，如果必要观测量相同，总观测量越多，所需要的系数矩阵的维度相对一般就越少，计算的复杂度就越低。最终解算的速度就越快。

2.2 基于间接平差的多项式拟合法

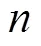
3 仿真分析

3.1 仿真条件设置

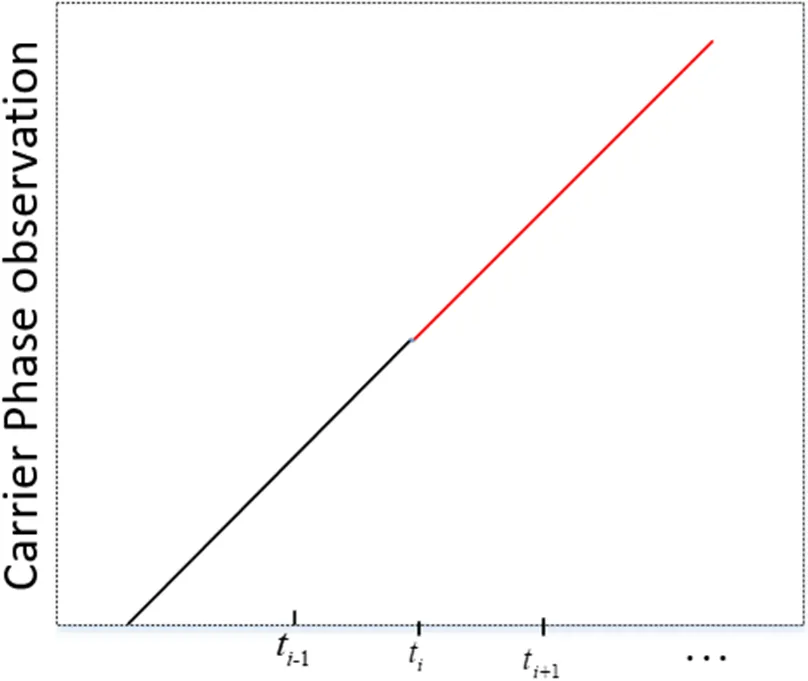
图1 载波相位周跳示意图

针对多项式拟合法探测周跳时，使用最小二乘法进行计算的问题。将算法分为一般算法和间接平差法求解。通过设置不同的环境，来仿真对比基于两种不同平差理论的多项式拟合算法，分析并判断算法的适用性及结算速度。

3.2 仿真结果分析

多项式拟合的阶数设定为2阶。仿真主要通过对比多项式拟合法中一般最小二乘法与间接平差法在不同观测值数据及多余观测量不同的情况下算法性能的不同。

当阶数确定时，此时的多项式拟合求解参数所需要的最少方程组数同时确定，冗余观测量就影响算法的计算效率。

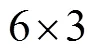
表1 算法解算速度分析

Tab.1 Calculation speed of algorithm

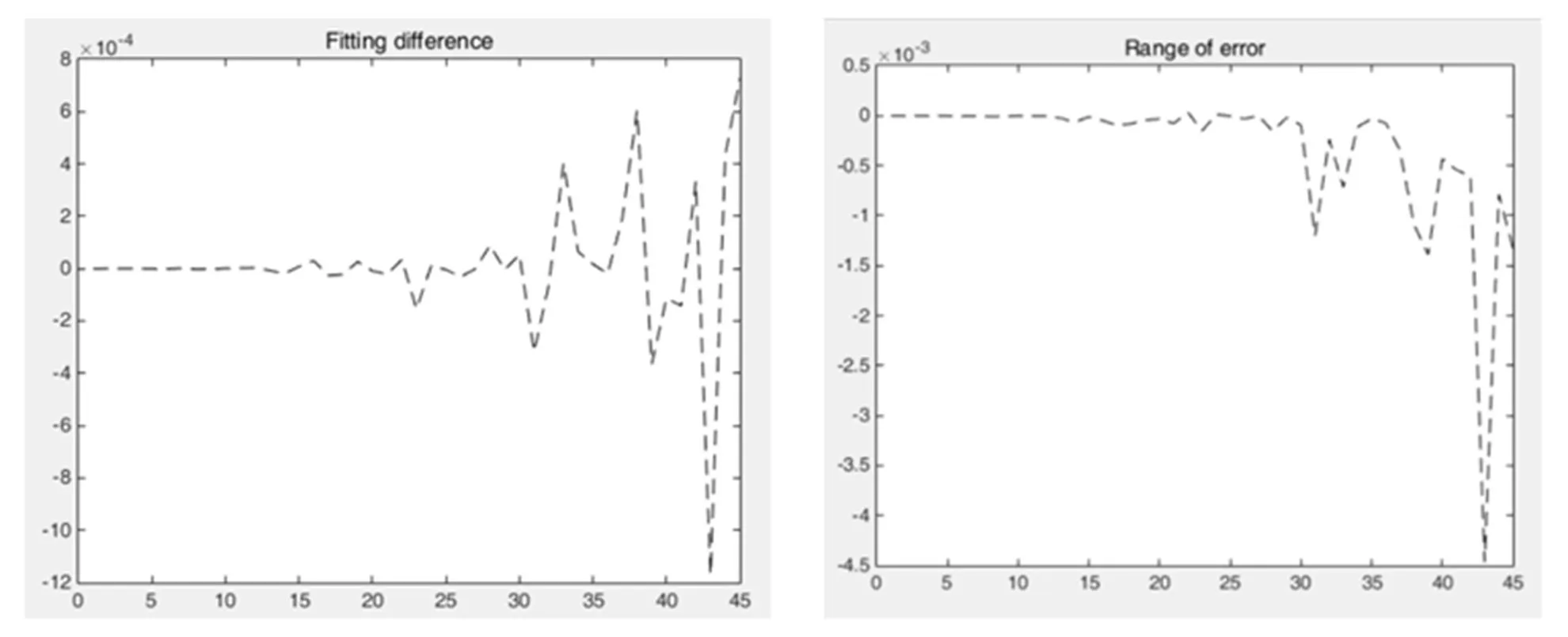
图2 算法解算性能分析

表2 算法解算速度分析

Tab.2 Calculation speed of algorithm

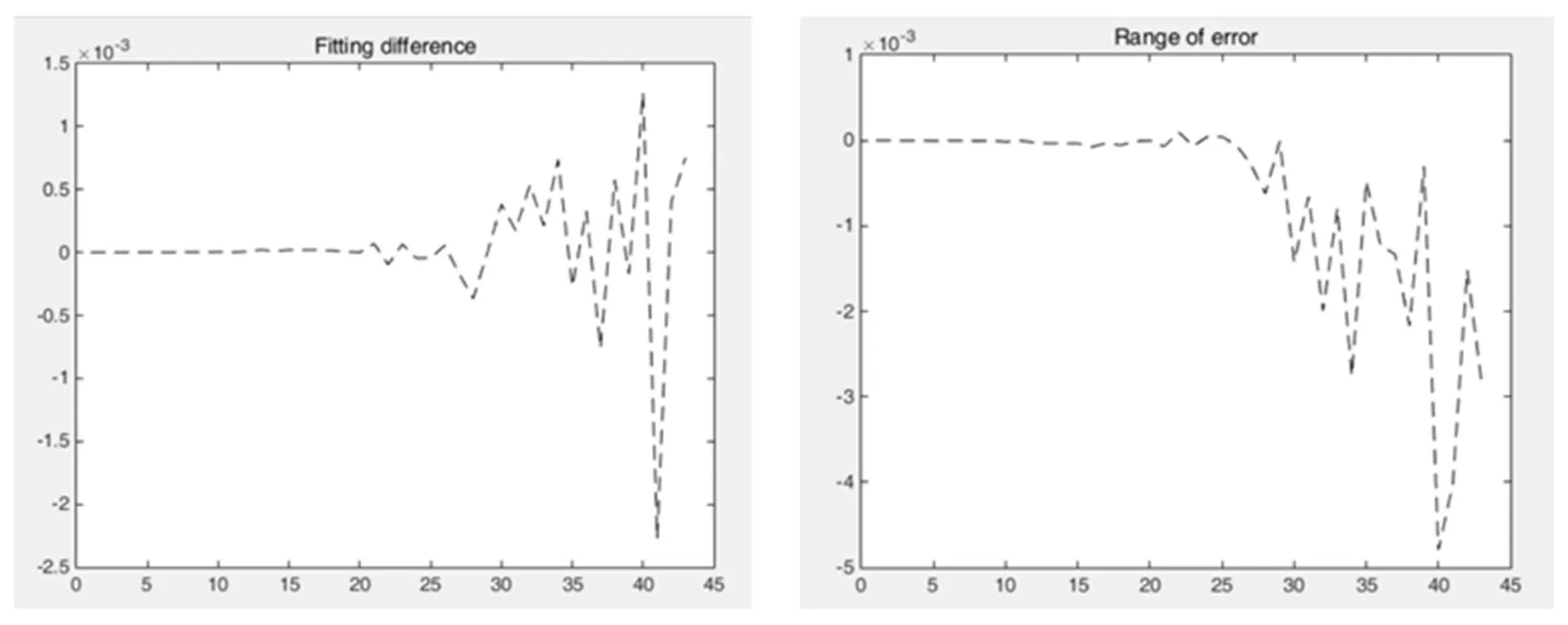
图3 算法解算性能分析

表3 算法解算速度分析

Tab.3 Calculation speed of algorithm

图4 算法解算性能分析

表4 周跳探测及判决误差

Tab.4 Cycle detection and decision error

对比三种算法之间的差别，可以看出。虽然算法有较快的速度，但是当矩阵位数维数越多时，其中包含错误信息的概率就会降低，发生错误判断 的可能性就会降低。维度越高，他将自变量继续细分成，用于仿真更多点数点数的的载波相位周跳 问题。

表5 算法解算时间分析

Tab.5 Calculation time of algorithm

图5 算法解算性能分析

表6 算法解算时间分析

Tab.6 Calculation time of algorithm

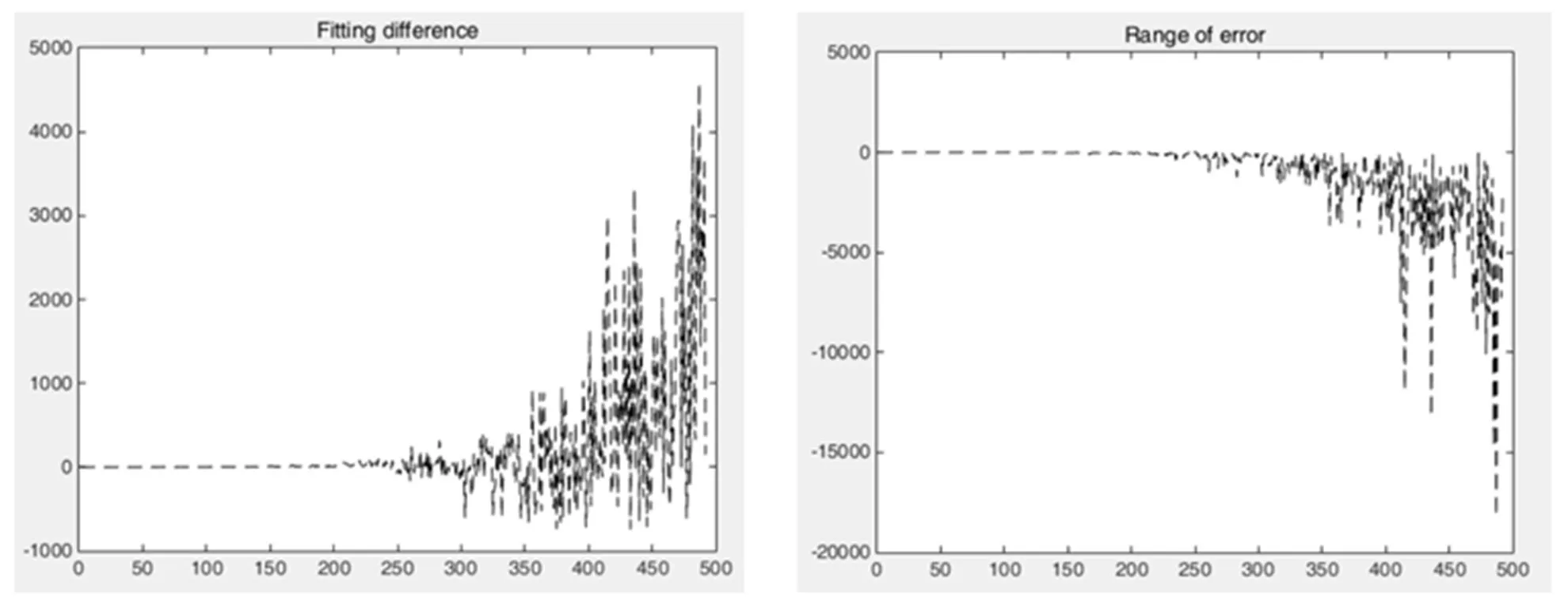
图6 算法解算性能分析

表7 算法解算时间分析

Tab.7 Calculation time of algorithm

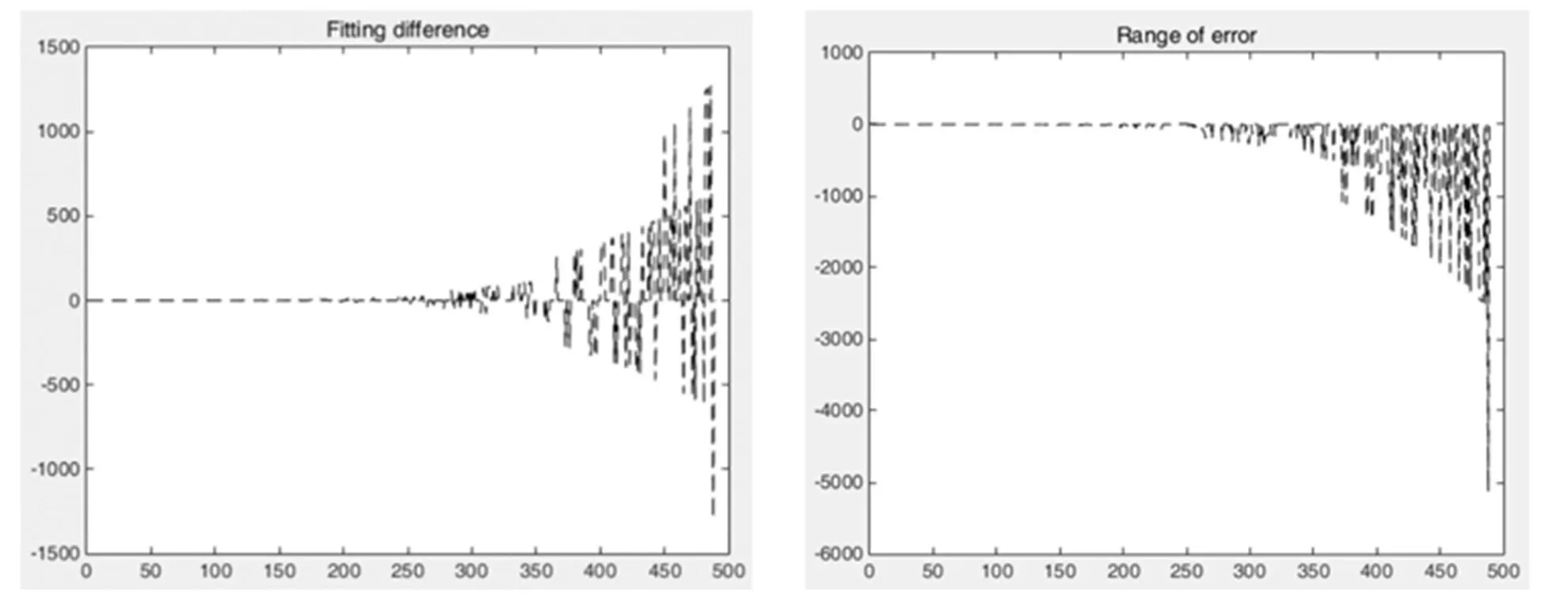
图7 算法解算性能分析

当载波相位观测值的数目十分巨大时，此时的算法维度过高。反而会大大影响。

在载波相位值特别多时，间接平差法的速率要差于一般最小二乘，而且解算的稳定度也差于一般最小二乘。

对于载波相位观测点较少时，间接平差法能较好的提高解算的效率，但是判断的稳定度较差。在观测点数较多时，间接平差法的各项性能都差于一般最小二乘。

4 结论

载波相位周跳检测是解决由于环境或自身原因产生的载波相位周跳，提高最终解算的成功率以及正确率的的一个重要方法，通过仿真可以发现，基于间接平差法的多项式拟合载波相位周跳探测能在一定的程度上提高周跳探测的效率。并为后续的载波相位整周模糊度解算和定位的实时性提供了一定保障。由于必要观测值的选取会导致解算的稳定性会出现很大的的变化，在未来的研究中可以着力研究这个方面的问题。

[1] Hk L, Wang J, C R. Effective Cycle Slip Detection and Identification for High Precision GPS/INS Integrated Systems[J]. Journal of Navigation, 2008, 56(3): 475-486.

[2] Ge M, Gendt G, Rothacher M, et al. Resolution of GPS carrier-phase ambiguities in Precise Point Positioning (PPP) with daily observations[J]. Journal of Geodesy, 2008, 82(7): 389-399.

[3] Cycle-slip[J]. Dictionary Geotechnical Engineering/wörterbuch Geotechnik, 2014:328-328.

[4] Vamos C, Craciun M. Polynomial Fitting[M]// Automatic trend estimation. Springer Netherlands, 2012: 31-42.

[5] Polynomial Fitting Method Improved Cycle Slip Detection[J]. Pioneering with Science & Technology Monthly, 2013.

[6] Teeuwsen J W M C, Soons J A, Schellekens P H J, et al. A General Method for Error Description of CMMs Using Polynomial Fitting Procedures[J]. CIRP Annals - Manufacturing Technology, 1989, 38(1):505-510.

[7] Tan F, Xu B, Wang C. Cycle Slips Detection and Correction of GPS Based on Carrier Phase Differences and Polynomial Fitting[J]. International Journal of Advancements in Computing Technology, 2013.

[8] Fang R, Shi C, Wei N, et al. Real-time cycle-slip detection for quality control of GPS measurements[J]. Geomatics & Information Science of Wuhan University, 2009, 34(9): 1094-1097.

[9] Zhang D. Application of Point Relaxation Method in Indirect Adjustment of Observation Equations[J]. Journal of Kunming Metallurgy College, 2000.

[10] Corbalis C, Bowers J E, Yuan S, et al. Method and apparatus for indirect adjustment of optical switch reflectors: US, US6819815[P]. 2004.

[11] Thorpe K E. The use of regression analysis to determine hospital payment: the case of Medicare's indirect teaching adjustment.[J]. Inquiry A Journal of Medical Care Organization Provision & Financing, 1988, 25(2):219.

[12] Astolfi R, Ladiray D, Mazzi G L. Business Cycle Extraction of Euro-Zone GDP: Direct versus Indirect Approach[J]. Vierteljahrshefte Zur Wirtschaftsforschung, 2001, 70(3): 377-398.

[13] Maravall A. An application of the TRAMO-SEATS automatic procedure; direct versus indirect adjustment[M]. Elsevier Science Publishers B. V. 2006.

[14] Shin H H, Cakmak S, Brion O, et al. Indirect adjustment for multiple missing variables applicable to environmental epidemiology.[J]. Environmental Research, 2014, 134: 482-487.

[15] Richardson D B, Laurier D, Schubauerberigan M K, et al. Assessment and indirect adjustment for confounding by smoking in cohort studies using relative hazards models.[J]. American Journal of Epidemiology, 2014, 180(9):933.

Little Cycle Slip Detection and Identification Based on Polynomial Fitting

ZHANG Sheng-ge, CHENG Nai-ping, NI Shu-yan

(Department of electronic and optical engineering of the University of Space Engineering, Beijing 101400, China)

This paper analyzes the cycle slip in the carrier phase observation. Comparing the High order difference method and the polynomial fitting method. And put forward a method based on the Indirect adjustment method. The simulation of the different method in order to find a well way to solve the cycle slip problem. The new method have a good speed in detecting the cycle clip.and can be used in next Calculation.

Carrier phase observation; Cycle slip; Indirect adjustment; Polynomial fitting

P228

A

10.3969/j.issn.1003-6970.2018.08.034

张晟歌(1994-)，男，研究生，主要研究方向：导航与信号处理；程乃平(1963-)，男，教授，主要研究方向：导航与信号处理；倪淑燕(1981-)，女，副教授，主要研究方向：飞行器测量与控制。

本文著录格式：张晟歌，程乃平，倪淑燕. 基于间接平差多项式拟合的周跳检测[J]. 软件，2018，39（8）：167-173