多重自适应卡尔曼滤波PMLSM无传感控制

孟祥宾，朱 军，李紫豪，刘炳辰



多重自适应卡尔曼滤波PMLSM无传感控制

孟祥宾，朱 军，李紫豪，刘炳辰

（河南理工大学电气工程及其自动化学院，河南 焦作 454000）

为了解决PMLSM无传感在运行控制中噪声的不确定性和滤波发散问题，本文提出一种改进的Sage-Husa自适应滤波器。针对Sage-Husa自适应滤波器存在抗干扰能力差和精度不高等问题，加入自校正状态滤波器。从理论上分析该算法的收敛性，证明该算法在一定条件下有界收敛。为验证该算法的有效性，将改进的EKF与传统EKF进行对比，结果表明本文提出的PMLSM多重自适应算法位置估计更加精确，克服了对噪声协方差矩阵的依赖性，增强了对突变状态的快速跟踪能力，速度估计误差百分比降低在0.1218%以下。

PMLSM；卡尔曼滤波；自适应；自校正

0 引言

随着空间技术和电子技术的发展及高速电子计算机的出现，要求处理复杂的多变量系统，时变系统及非平稳随机过程，要求实时、快速计算最优滤波器[1]。在这种应用背景下，出现了诸多无传感算法[2-4]，R.E.Kalman突破了经典Wiener滤波方法的局限性，提出了时域上的Kalman滤波方法[5-6]。Kalamn最初提出的滤波理论只适用于线性系统，Sunahara等人提出并研究了扩展卡尔曼滤波[7-10]，将Kalman滤波理论进一步应用到非线性领域。为了加强历史数据的影响，又出现了多新息理论卡尔曼滤波[11-14]，卡尔曼滤波方法的缺点和局限性是它要求已知系统的精确数学模型和噪声统计。在大部分实际问题中，数学模型或噪声统计是完全或部分未知的，或近似已知的（即含有模型误差或噪声统计误差，也称为含有未建模动态）。在这种情形下不能直接应用经典的Kalman滤波方法，否则应用错误的数学模型或错误的噪声统计将引起Kalman滤波器性能变坏，甚至导致滤波发散。为了克服经典Kalman滤波的上述缺点和局限性，产生了Kalman滤波理论的一个分支—自适应卡尔曼滤波[15-20]。本文提出一种改进的Sage- Husa自适应滤波器，解决含有未知模型参数和噪声统计系统或含有未建模动态系统的滤波问题。通常用噪声统计估计器或模型参数估计器伴随Kalman滤波器实现自适应Kalman滤波，但噪声统计或模型参数估计器与状态估计值器是互耦的，容易出现滤波发散现象, 广东工业大学高向东等人提出一种有效抑制滤波发散的方法[21]。针对自适应卡尔曼滤波存在的上述问题，本文在自适应基础上提出了一种自校正卡尔曼滤波理论和方法[22-24]，黑龙江大学白锦花等人应用该算法，有效得克服了滤波发散并提高滤波精度。

1 PMLSM的等效模型

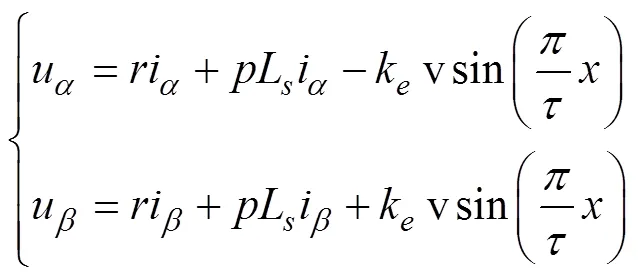
状态方程为：

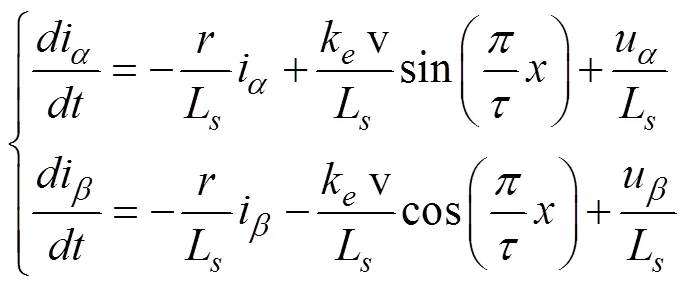
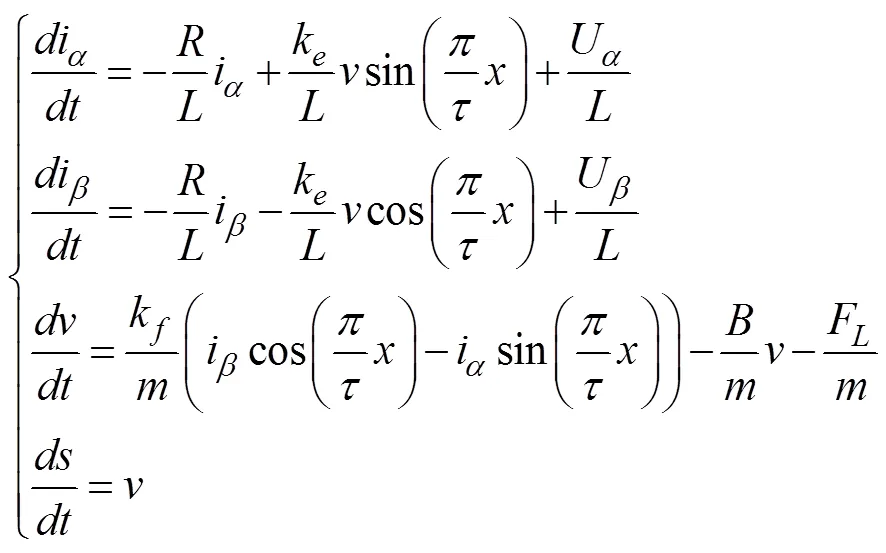
可将（3）写成矩阵形式如下：

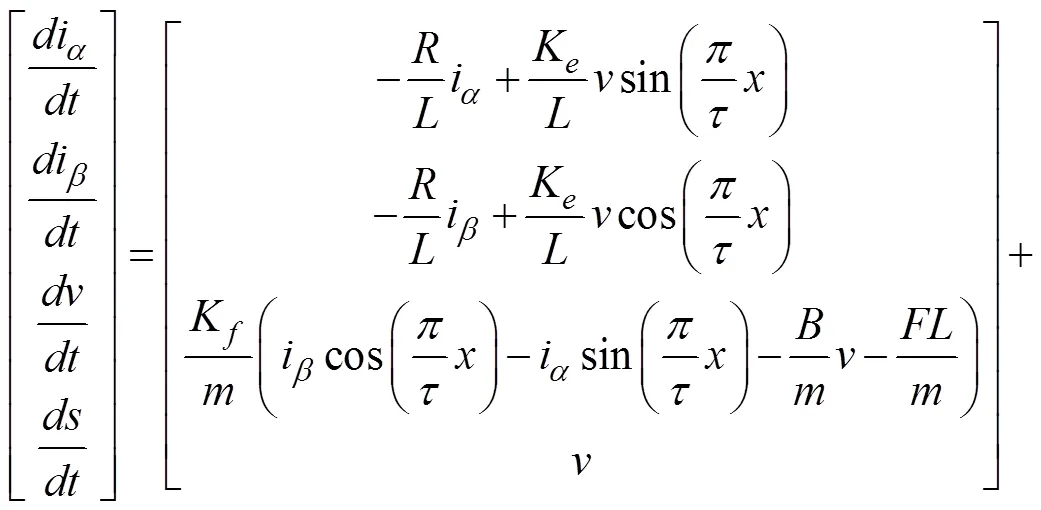
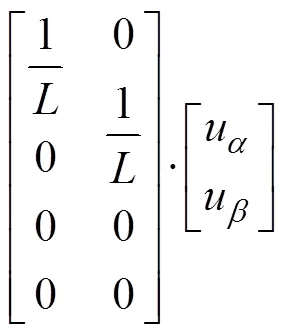
式（4）可简化为：

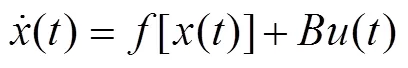
其中

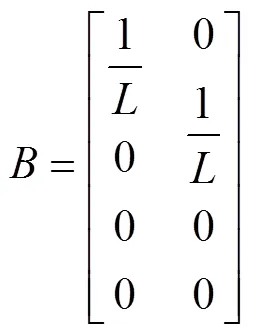
上式为PMLSM最终等效模型，将该模型应用在卡尔曼滤波器中进行预测、修正，不断的迭代来实现最终目的。

2 多重自适应卡尔曼滤波在PMLSM中应用

采用基本卡尔曼滤波和扩展卡尔曼滤波方法估计PMLSM运行参数时，一般假定噪声为零均值白噪声，且噪声方差已知。在噪声确定情况下，基本卡尔曼滤波和扩展卡尔曼滤波方法的估计效果很好，但实际上白噪声不存在。

系统对应的非线性方程表示如下：

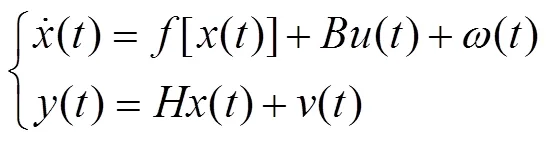
PMLSM系统是一个非线性系统，将该系统展开成Taylor级数并略去二阶及以上项得到近似线性化模型，根据线性理论将其离散化的模型可表示为：

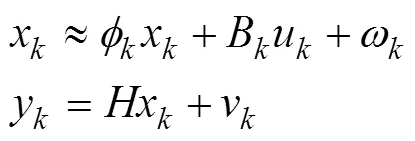
其中，

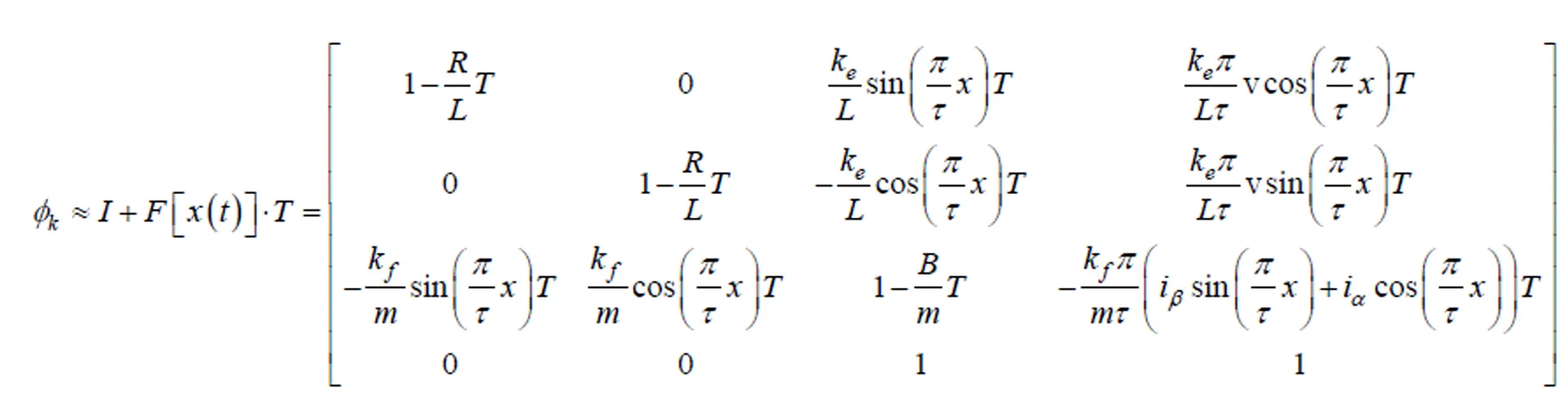
在上述离散化的模型上建立仿真模型，将改进的Sage-Husa时变噪声统计器和自校正状态估计器结合实现多重自适应滤波。

卡尔曼滤波利用测量数据不断地在线估计噪声的均值以及方差，使用更新后的状态不断替换当前的状态估计值，实现对估计状态量和噪声统计量的交替更新。本文利用改进的Sage-Husa自适应卡尔曼滤波器，把扩展卡尔曼滤波中由于线性化引起的模型误差归入到带未知时变均值和方差的虚拟噪声中去。根据文献[1]有改进的Sage-Husa时变噪声统计递推估值器：

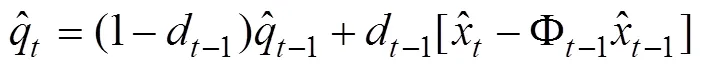
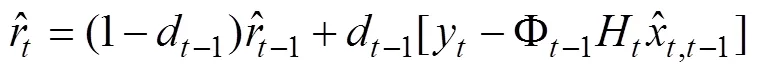
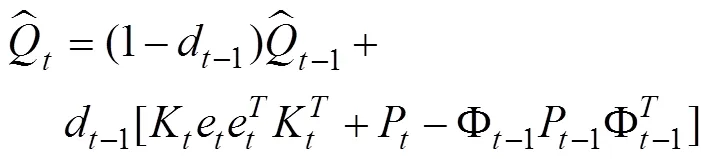
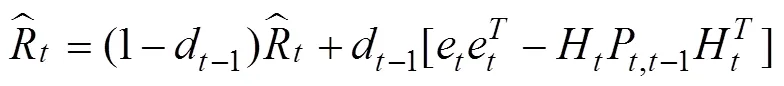
根据改进的Sage-Husa算法，假设噪声均值q和r和方差阵Q和R未知的，且q和r不为0。将式Sage-Husa时变噪声统计器引入得到线性化、离散化后的卡尔曼滤波的公式：

（1）由k-1时刻的状态和误差协方差矩阵对k时刻不确定性的状态和误差协方差矩阵进行时间更新。

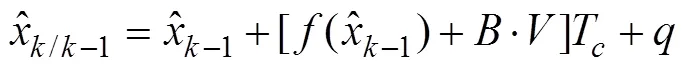
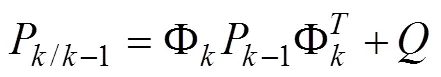
（2）卡尔曼滤波增益：

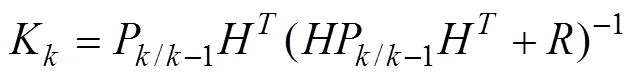
如果当前状态估计误差大，则会使P变大，从而使增益K也相应变大，致使系统大幅度地更新状态，从公式（14）可以看出，增益矩阵公式可以离线计算。

（3）根据文献[1]和文献[20]，自校正卡尔曼滤波器有渐进最优的特点，在状态估计中引入自校正卡尔曼滤波器。利用观测数据对系统状态进行更新并且更新误差协方差矩阵。

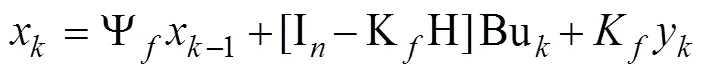
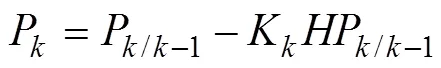
由上分析，不断地对qk，rk，Qk和Qk进行实时估计来达到对状态变量估计值x的不断修正从而实现高精度的滤波。

3 改进后卡多重自适应尔曼滤波器的收敛性分析

考虑改进算法动态系统

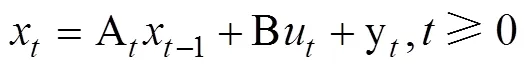
将式（17）分解分解如下：

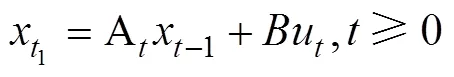
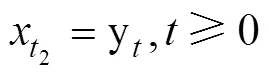
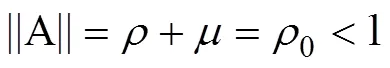
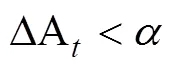
由（18）迭代有关系式，

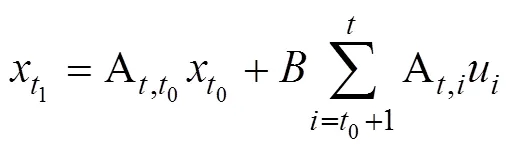
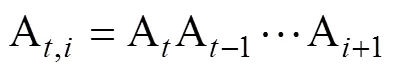
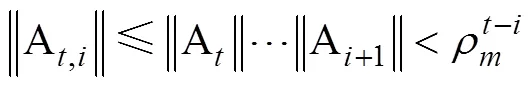
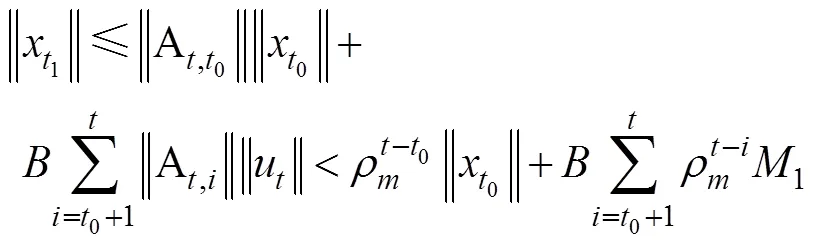
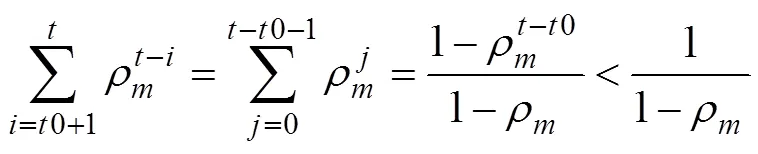
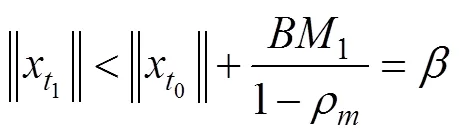
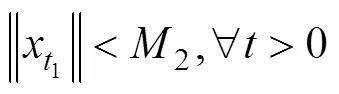
4 仿真分析

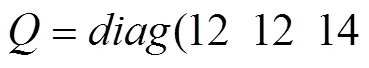
下图为EKF在PMLSM中的仿真结果，同步速度参数分别选择0.468 m/s和1.22 m/s，通过速度和误差曲线来判断EKF在直线电机中的收敛性和精度。

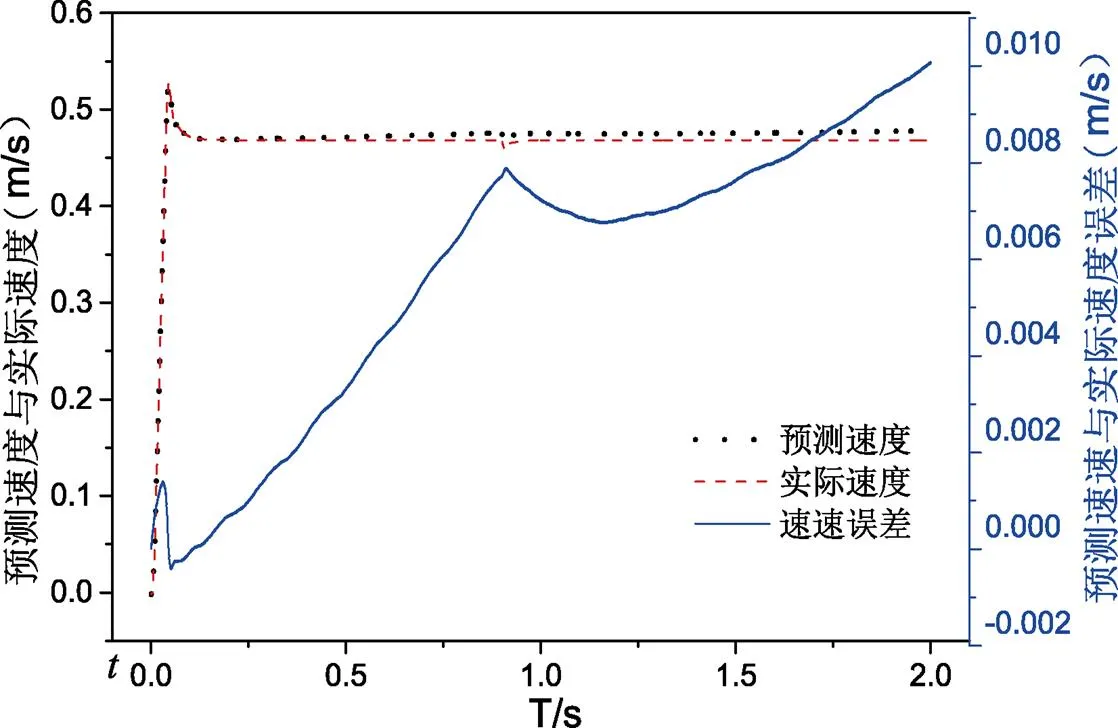
图1 PMLSM在0.48 m/s时的实验结果

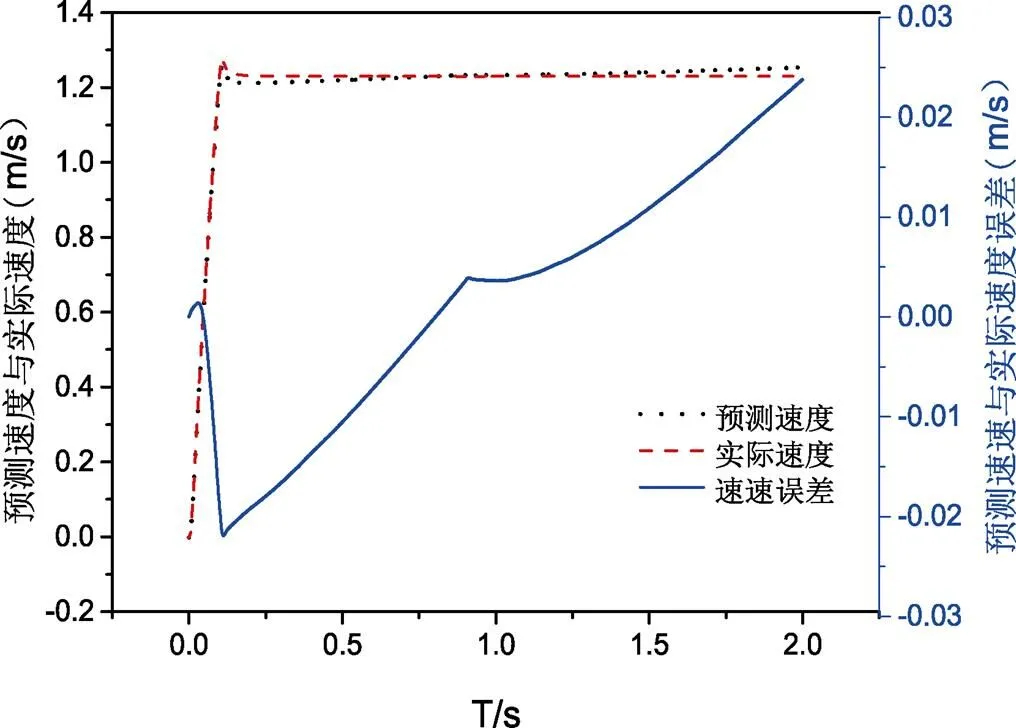
图2 PMLSM在1.22 m/s时的实验结果

由图1和图2可知，由于PMLSM本身结构和EKF存在的问题，使得预测跟踪能力随着仿真时间的增长，而出现发散现象。以0.48 m/s的同步速度运行时，在仿真达到2 s时，预测误差为0.01 m/s；以同步速度1.23 m/s的同步速度运行时，在仿真达到2 s时，预测误差值已经达到0.025 m/s。由此可见，PMLSM在高速时发现现象尤为明显。为了克服滤波发散以及精度问题，提出了多重自适应卡尔曼滤波器。

本文分别采用EKF与多重自适应卡尔曼滤波算法进行对比分析。分析了速度估测、位置估测以及误差精度。图3和图4分别表示多重自适应卡尔曼滤波的速度和位置估测，图5和图6为改进后算法的速度误差分析和对比。速度检测中，图3中多重自适应算法曲线围绕实际曲线上下波动，在0.9 s突加负载，由500 N·m突变到700 N·m，改进算法速度曲线依然紧贴着实际曲线。因此，该算法体现出波动小，抗扰能力强的优点；位置检测中，局部放大图上显示，改进的算法更接近实际位置。

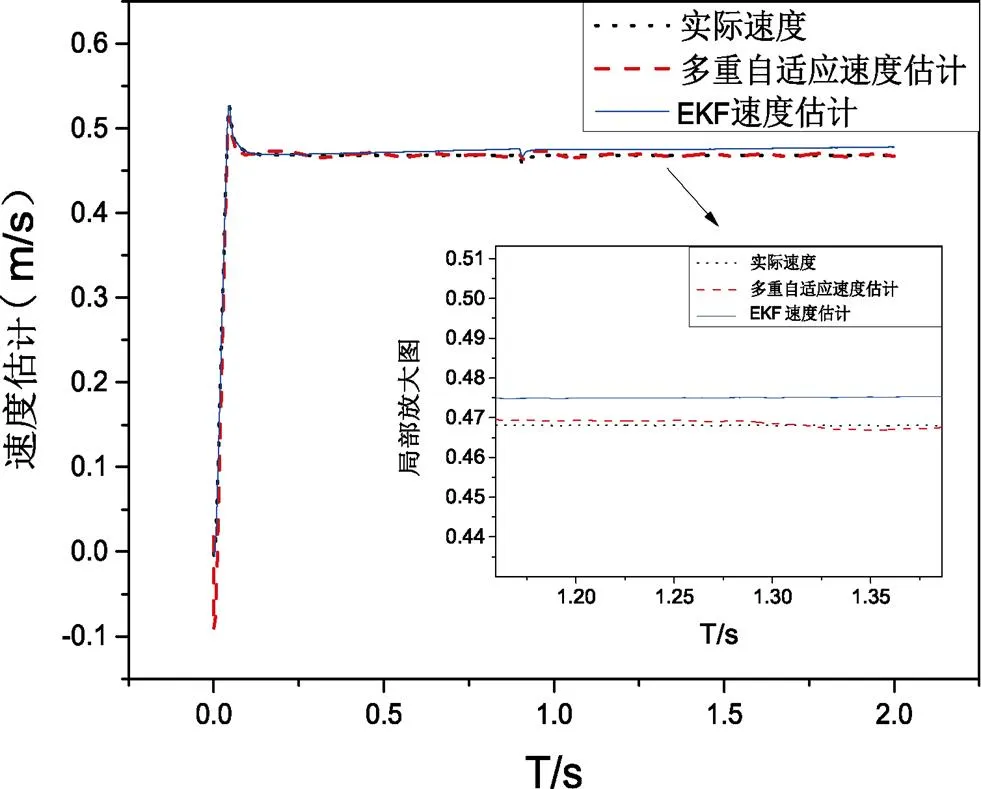
图3 多重自适应算法与EKF算法速度跟踪对比

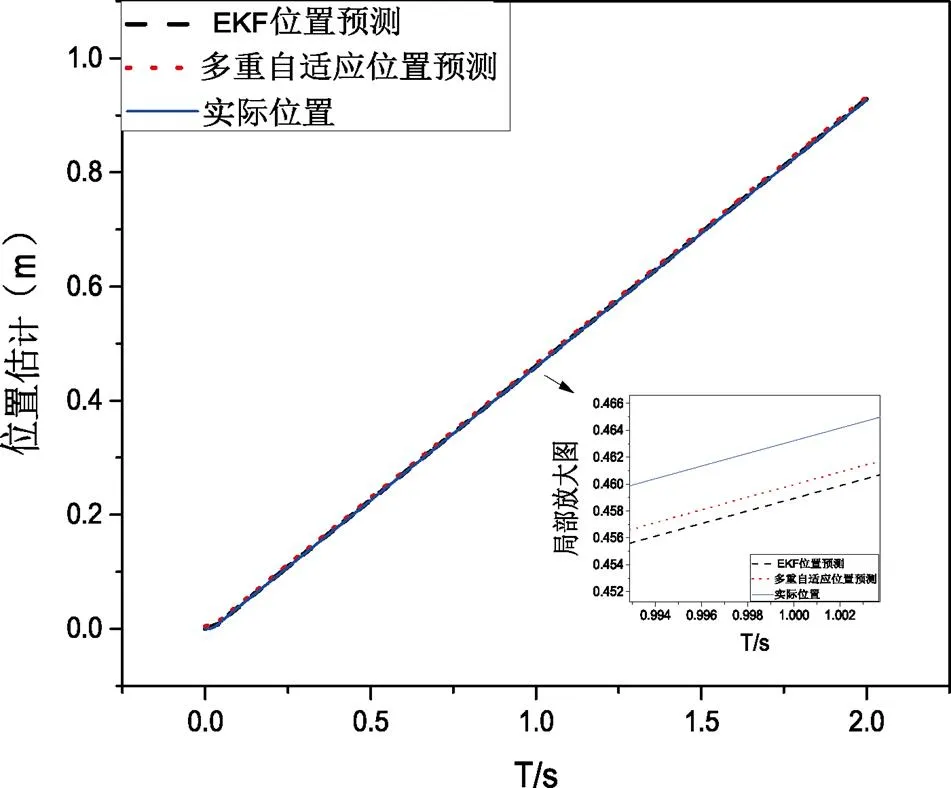
图4 多重自适应算法与EKF算法位置跟踪对比

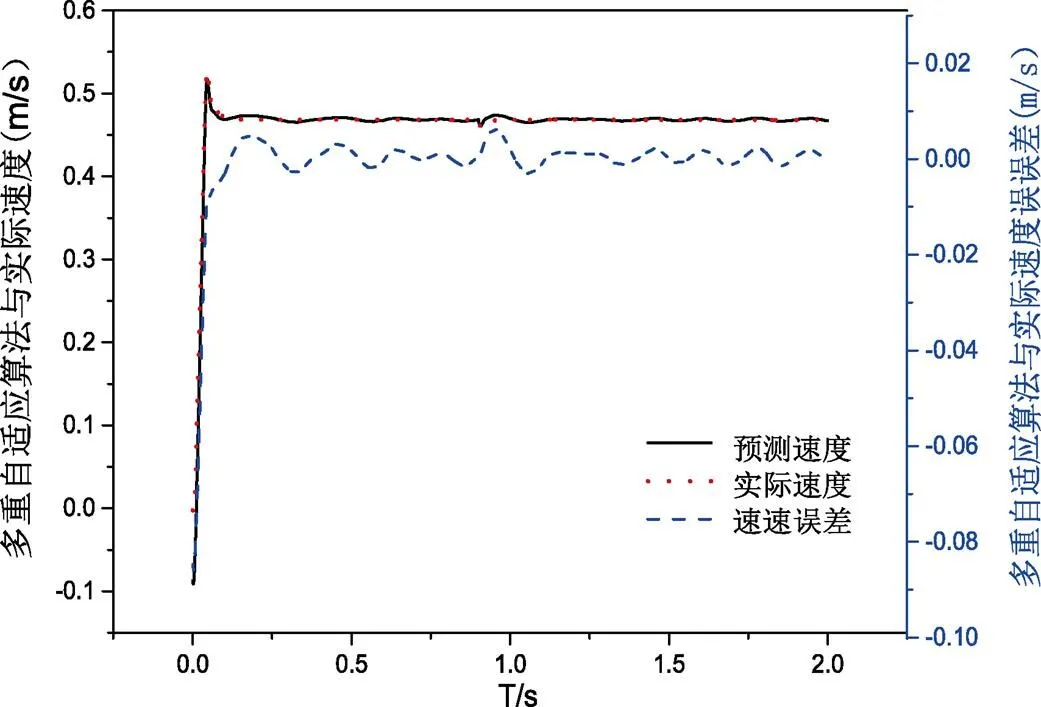
图5 多重自适应算法与实际速度误差分析

图6 多重自适应算法与EKF算法速度误差曲线

图5和图6显示，改进后的算法波动非常小，在突加负载后，能够快速恢复至稳定运行，且改进后的算法整体误差要小于EKF，电机启动时，最大误差为0.46%，突加负载后，波动最大误差为0.37%，稳定运行时最大误差为0.12%。故改进后的算法更接近真实值，精度高，鲁棒性强。

5 结论

本文基于EKF算法，并使用多重自适应卡尔曼滤波理论进行改进，分别进行了收敛性理论上的分析及改进后的实验验证。结果表明多重自适应卡尔曼滤波比原来的扩展卡尔曼滤波辨识精度更高，稳定性更强，加负载后快速收敛，速度波动误差降低到0.37%，稳定后最大误差可以有效的控制在0.12%以下。因此，本文的多重自适应卡尔曼滤波更能准确地描述PMLSM的运动，达到抗干扰能力强，误差小的目的。

[1] 邓自立. 自校正滤波原理及其应用[M]. 哈尔滨: 哈尔滨工业大学出版社, 2003.

[2] 陈晓燕, 姚高伟, 张鲲, 等. 基于遗传算法的无线传感器节点定位在农业的应用[J]. 软件, 2015, 36(4): 1-5.

[3] 聂敬云, 李春青, 李威威, 等. 关于遗传算法优化的最小二乘支持向量机在MBR 仿真预测中的研究[J]. 软件, 2015, 36(5): 40-44.

[4] 沙娓娓, 刘增力. 基于改进蚁群算法的无线传感器网络的路由优化[J]. 软件, 2018, 39(01): 01-04.

[5] 潘迪夫, 刘辉, 李燕飞. 基于时间序列分析和卡尔曼滤波算法的风电场风速预测优化模型[J]. 电网技术, 2008(07): 82-86.

[6] 潘迪夫, 刘辉, 李燕飞. 风电场风速短期多步预测改进算法[J]. 中国电机工程学报, 2008(26): 87-91.

[7] 陈振, 刘向东, 靳永强, 戴亚平. 采用扩展卡尔曼滤波磁链观测器的永磁同步电机直接转矩控制[J]. 中国电机工程学报[J]. 2008(33): 75-81.

[8] 薛长虎, 聂桂根, 汪晶. 扩展卡尔曼滤波与粒子滤波性能对比[J]. 测绘通报[J]. 2016(04): 10-14.

[9] 庄旭, 戈宝军, 陶大军. 基于分块Hankel矩阵的抽水蓄能电机扩展卡尔曼滤波模型子空间循环辨识[J]. 中国电机工程学报, 2017, 37(24): 7328-7337+7447.

[10] G. Yu. Kulikov, M. V. Kulikova. Accurate cubature and extended Kalman filtering methods for estimating continuous- time nonlinear stochastic systems with discrete measurements[J]. Applied Numerical Mathematics, 2017, 111.

[11] 刘毛毛, 吕国宏, 常江. 基于多新息理论的卡尔曼滤波改进算法[J]. 中北大学学报(自然科学版), 2015, 36(02): 234-239.

[12] 高向东, 许二娟, 李秀忠. 多新息理论优化卡尔曼滤波焊缝在线识别[J]. 焊接学报, 2017, 38(03): 1-4+129.

[13] 李雅梅, 康璐璐. 多新息抗差——自适应卡尔曼滤波定位算法研究[J]. 传感器与微系统, 2017, 36(09): 38-40+44.

[14] 谢朔, 陈德山, 初秀民, 柳晨光. 改进多新息卡尔曼滤波法辨识船舶响应模型[J]. 哈尔滨工程大学学报, 2018, 39(02): 282-289.

[15] 李雅梅, 康璐璐. 多新息抗差——自适应卡尔曼滤波定位算法研究[J]. 传感器与微系统, 2017, 36(09): 38-40+44.

[16] 杨春, 郭健, 张磊, 陈庆伟. 采用卡方检验的模糊自适应无迹卡尔曼滤波组合导航算法[J]. 控制与决策, 2018, 33(01): 81-87.

[17] Fan Z, Sun Q, Du L, et al. Application of adaptive Kalman filter in vehicle laser Doppler velocimetry[J]. Optical Fiber Technology, 2018, 41: 163-167.

[18] ZHAO Lin, LI Jiushun, CHENG Jianhua. Innovation-based adaptive Kalman filter with sliding window for integrated navigation[J]. Systems Engineering and Electronics, 2017, 39(11): 2541-2545.

[19] Zhang Y, Yin Z, Li G, et al. A novel speed estimation method of induction motors using real-time adaptive extended kalman filter[J]. Journal of Electrical Engineering & Technology, 2018, 13(1): 287-297.

[20] 陈政, 刘康. 闪烁噪声下的自适应无迹卡尔曼算法[J]. 软件, 2018, 39(01): 70-74

[21] 高向东, 张驰, 周晓虎. 微间隙焊缝磁光成像NN-KF跟踪算法[J]. 焊接学报, 2017, 38(01): 9-12+129.

[22] 白锦花. 带未知随机系统偏差的最优与自校正信息融合滤波器[A]. 中国自动化学会控制理论专业委员会(TechnicalCommittee on Control Theory, Chinese Association of Automation).第二十六届中国控制会议论文集[C]. 中国自动化学会控制理论专业委员会(Technical Committee on Control Theory, Chinese Association of Automation): 2007: 5.

[23] 陶贵丽, 邓自立. 含未知参数的自校正融合Kalman滤波器及其收敛性[J]. 自动化学报, 2012, 38(01): 109-119.

[24] 李俊, 王雪平, 张福斌. 基于自校正卡尔曼滤波器的信息融合算法[J].

Multiple Adaptive Calman Filters for PMLSM Sensorless Control

MENG Xiang-bin, ZHU Jun, LI Zi-hao, LIU Bing-chen

(School of electrical engineering and automation, Henan Polytechnic University, Jiaozuo, Henan 454000, China)

In order to solve the problem of noise uncertainty and filtering divergence in the operation control of PMLSM model, an improved Sage-Husa adaptive filter is proposed. In order to solve the problem of poor anti-interference ability and low precision in Sage-Husa adaptive filter, a self-tuning state filter is added. The convergence of the algorithm is analyzed theoretically, and it is proved that the improved algorithm has a bounded convergence under certain conditions. To verify the effectiveness of the algorithm, the improved algorithm is compared with the traditional EKF, the results show that the location of multiple adaptive algorithm proposed PMLSM estimation is more accurate, and the noise covariance matrix dependence, enhance the fast tracking ability of the mutation status, the percentage error decreased below 0.1218% speed estimation.

PMLSM; Calman filter; Adaptive; Self-tuning

TP273+.2

A

10.3969/j.issn.1003-6970.2018.08.005

河南省高校基本科研业务费专项资金资助项目(NSFRF140115)；河南省教育厅科学技术重点研究项目(12A470004)；河南省控制工程重点学科开放实验室开放基金(KG2011-12)

朱军(1984-)，男，副教授，硕士生导师，研究领域为特种电机驱动；李紫豪(1991-)，男，硕士研究生，研究领域为特种电机驱动。刘炳辰(1993-)，男，硕士研究生，研究领域为特种电机驱动。

孟祥宾(1991-)，男，硕士研究生，研究领域为特种电机驱动。

本文著录格式：孟祥宾，朱军，李紫豪，等. 多重自适应卡尔曼滤波PMLSM无传感控制[J]. 软件，2018，39（8）：18-23