外包冷弯U形钢-混凝土T形组合梁受弯性能研究

吴钟艳 王人鹏 罗永峰 李伟兴 黄青隆 丁 一

(1.同济大学建筑工程系,上海 200092; 2.天华建筑设计有限公司,上海 200235)

0 引 言

钢与混凝土组合梁是现代结构工程中应用较为广泛的一类构件,兼有钢筋混凝土结构和钢结构的共同优点,是未来结构体系中的主要构件之一[1]。外包U形钢-混凝土T形组合梁是一种新型的钢与混凝土组合梁,继承了传统组合梁的优点,克服了传统组合梁的许多缺点[2-4],其综合性能优于普通组合梁[5-6],是一种值得推广应用的组合梁。目前,关于这类新型组合梁受力性能的研究,已有相关报道,主要研究内容包括组合梁抗正弯矩承载力[2,5,7-14]、抗负弯矩承载力[9,13-14]、抗剪承载力[10-11]、抗扭承载力[15]、钢与混凝土交界面滑移效应[5-6,9,16]以及采用高强钢和高强混凝土的新型组合梁受弯性能[17-19]等,并有学者推导出了变形和滑移计算的简单公式以及极限承载力计算公式。

为进一步拓展外包U形钢-混凝土T形组合梁的截面构造形式并完善其理论体系以适应不同工程需要,本文参考已有研究成果,并根据某实际住宅工程项目应用要求和现行国家标准,按照完全剪力连接设计方法[20]设计了一种新型组合梁,其外包U形钢是由薄壁钢板冷弯成形。冷弯U形钢的采用不仅可以避免钢板焊接带来的不利影响,而且便于工业化生产。本文通过3根新型组合梁足尺试件开展新型组合梁的受弯性能试验,研究其力学性能、破坏机理与破坏模式、极限承载能力以及钢板与混凝土共同作用机理,并用有限元软件进行了模拟,采用变参的分析方法研究了腹板混凝土和栓钉间距对组合梁性能的影响特征与变化规律。

1 试验研究

1.1 试验设计

本文设计制作了3根新型组合梁足尺试件。试件截面构造详见图1、图2,试件编号、几何尺寸和相关参数见表1。外包钢采用Q345B冷弯型材,钢筋采用HRB400,混凝土强度等级为C30。外包钢采用冷弯成形的方式不仅可以避免钢板焊接带来的不利影响,而且便于工业化生产。外包钢支托于钢筋混凝土板底,厚度为6 mm。外包钢上翼缘外翻,以保证内部混凝土的浇筑质量,相比外包钢上翼缘内翻,增加了翼缘板混凝土和梁内混凝土交界面的面积,同时可提高新型组合梁的纵向水平抗剪能力。梁内部设置8@200箍筋作为抗剪措施,可提高梁的纵向水平抗剪能力,使得剪力连接件的数量减少。在外包钢板翼缘和底板内壁焊接间距为200 mm的尺寸为13 mm×70 mm栓钉,以传递纵向剪力并增加抗拔力,栓钉材料性能等级为4.6级。试件内设下纵向钢筋212、上纵向钢筋416。试件混凝土、钢筋、钢板实测力学性能见表2、表3。

表1外包U形钢-混凝土T形组合梁试件参数

Table 1Designed parameters of U-shape steel encased concrete composite beam specimens

表2钢材的力学性能

Table 2Mechanical propertise of steel

表3混凝土的力学性能

Table 3Mechanical propertise of concrete

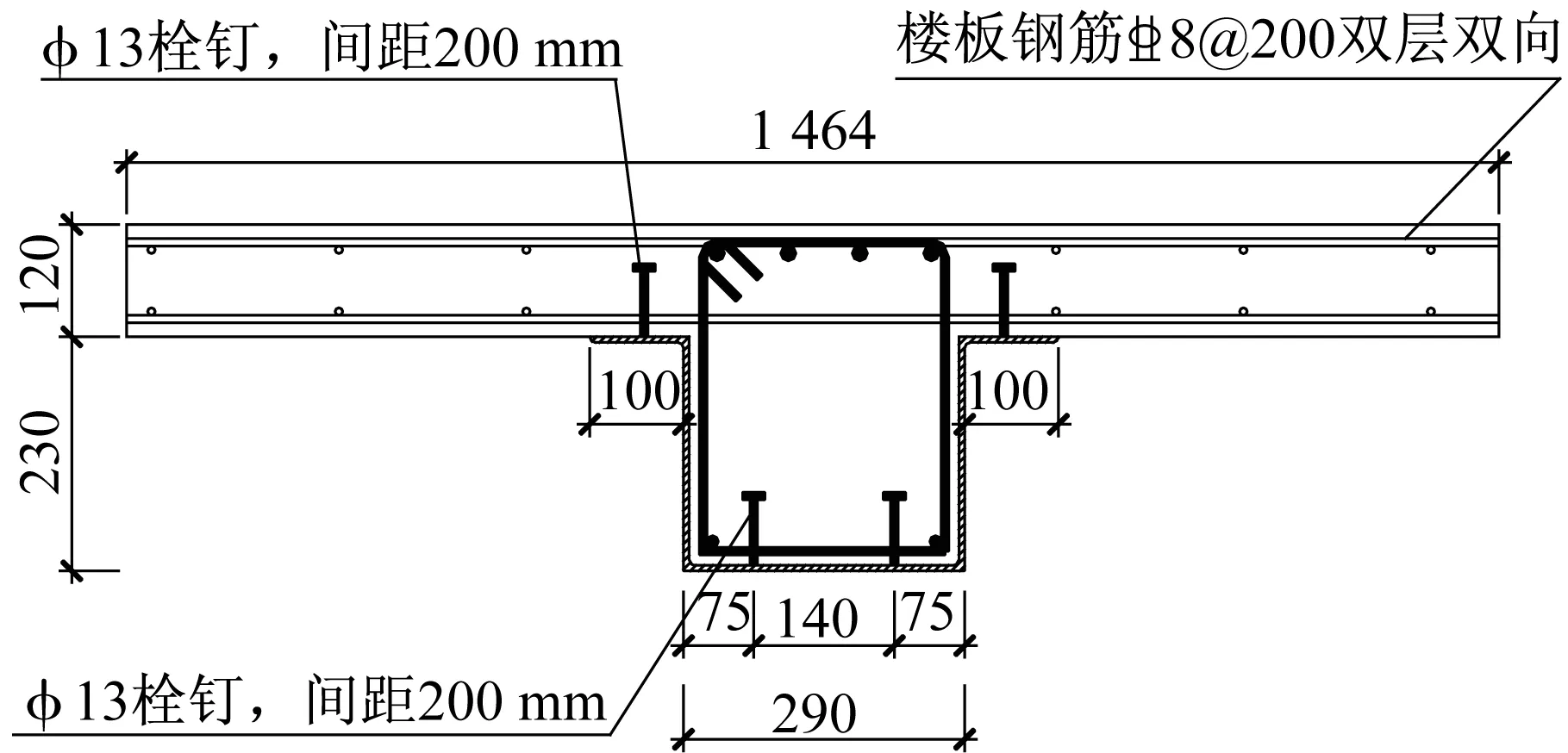
图1 组合梁截面构造Fig.1 Cross section of a composite beam

图2 外包U形钢和钢筋详图Fig.2 Detail of U-shape steel and reinforcement

1.2 试验加载及测点布置

新型组合梁试验为单调静力荷载试验,采用三分点对称加载。加载装置由200 t千斤顶、一级分配梁、二级分配梁、反力架等组成,如图3所示。正式加载前先分3级预加载至30 kN以检查试验装置是否正常工作。正式加载在预估特征荷载附近加密荷载步,以10 kN为一个加载步进行加载,以观测试验现象;其余步以20 kN为一个加载步进行加载;接近极限荷载时,采用位移控制缓慢持续加载直至试件破坏。试验测量的主要参数有:千斤顶荷载、加载点及跨中挠度、腹板外表面应力、翼缘板应力、钢板与混凝土的相对滑移以及支座沉降。千斤顶荷载由液压加载系统自动采集(力传感器采集),其余测量参数需布置应变片和位移计进行测量,应变片和位移计的具体布置方案如图4所示。

图3 加载方案示意图Fig.3 Schematic diagram of loading scheme

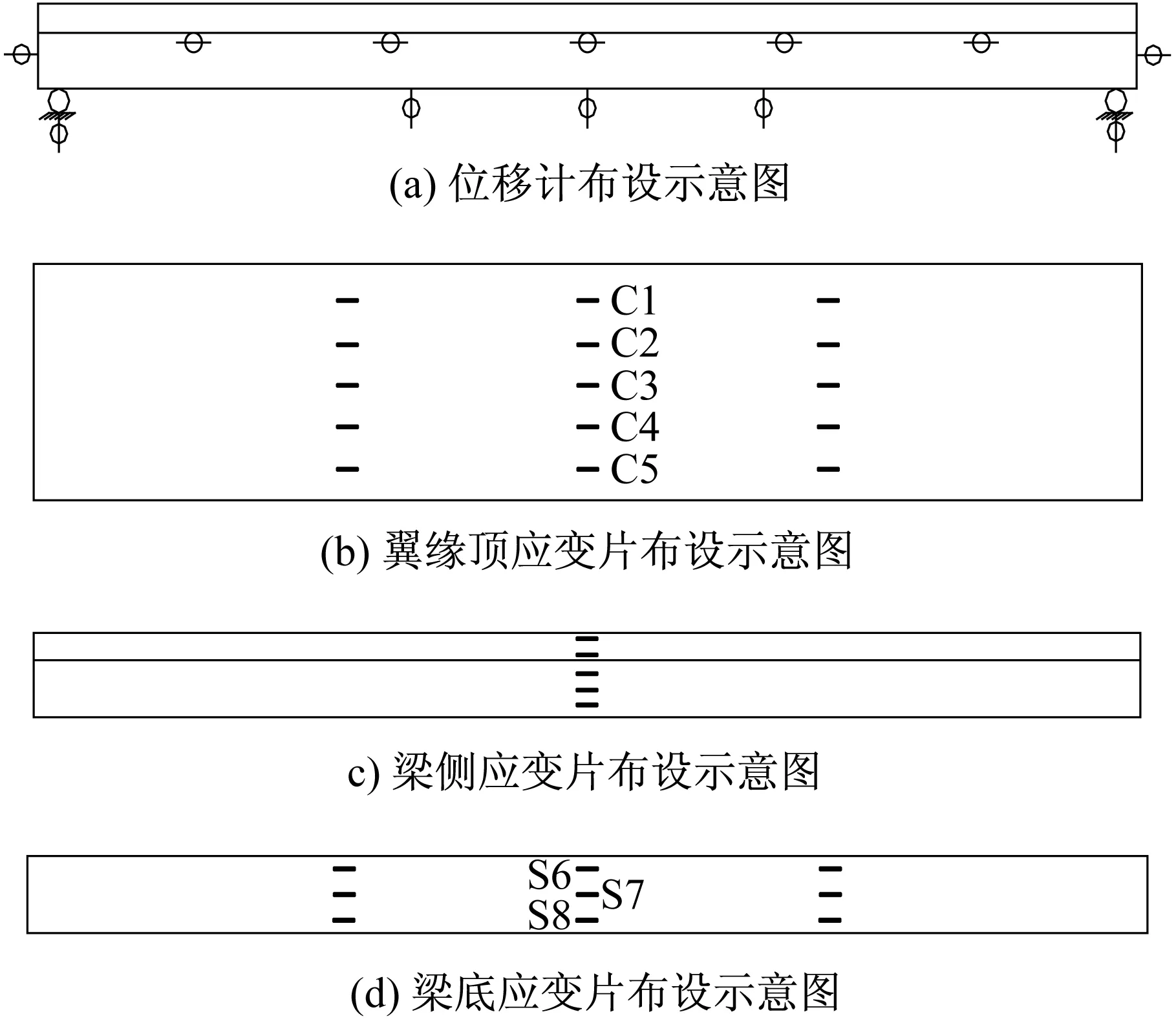
图4 测点布置示意图Fig.4 Schematic diagram of measurements

2 试验结果及分析

2.1 试验过程及破坏形态

在相同加载条件下3根试件的破坏特征相似,本节以试件SJ1为例进行说明。加载到0.12Fu(Fu为极限荷载值,由跨中挠度达到试件净跨的1/50时对应的单点加载值确定[21])时,试件出现轻微响声,表明钢板与混凝土接触面的自然黏结破坏;加载到0.24Fu时,加载点处混凝土翼缘板下表面出现横向裂缝;加载到0.57Fu时,外包钢的底板开始屈服,混凝土翼缘板下表面横向裂缝数量增加,分布范围逐渐增大;加载到0.77Fu时,试件持续出现较大响声,梁端钢板与混凝土出现明显滑移(图5);加载到0.95Fu时,跨中外包钢截面全部屈服;加载到1.0Fu时,试件挠度迅速增大,纯弯段混凝土翼缘横向裂缝急剧开展并不断向上延伸,加载点附近部分裂缝发展成为宽度较大的若干条主裂缝;最后,加载点附近混凝土突然压溃(图6),此时,纯弯段及加载点周围混凝土翼缘板底部已密布裂缝,且分布均匀(图7),裂缝形态主要以横向裂缝为主,混凝土翼缘板顶部有两条通长纵向裂缝(图8),位置处于钢板翼缘栓钉处附近,说明此为新型组合梁的一个薄弱部位,这是由于栓钉对其周围混凝土存在着较大的集中力作用,使得混凝土产生横向拉应力,当栓钉引起的混凝土的拉力增加至一定量值时,混凝土就产生了沿梁纵轴方向的劈裂裂缝。图9所示为试件的整体破坏形态。另外,钢板没有发生明显鼓曲,也未发生掀起变形。

图5 梁端钢板与混凝土发生相对滑移Fig.5 Relativeslip between steel and concrete

图6 混凝土翼缘被压溃Fig.6 Failure mode of specimens

图7 混凝土翼缘板底部横向裂缝Fig.7 The transversal cracks at the bottom of concreted flange

图8 混凝土翼缘板顶部产生纵向裂缝Fig.8 The longitudinal cracks at the top of concrete flange

图9 试件整体破坏形态Fig.9 Global damage of specimens

2.2 荷载-挠度曲线

新型组合梁的实测荷载-挠度曲线见图10,试验结果表明,新型组合梁的受力全过程可划分为四个阶段:混凝土开裂前阶段、混凝土开裂至钢板开始屈服前阶段、钢板开始屈服至极限荷载阶段、极限荷载后阶段。

图10 荷载-挠度曲线Fig.10 Load-deflection curve

1) 混凝土开裂前阶段

由于梁肋部外包钢板,因此,无法直接观察内部混凝土的开裂。实际上,在梁中有混凝土裂缝的截面,混凝土一旦开裂,就把原先承担的那一部分拉力转给外包钢,导致试件出现明显的应力重分布现象,即荷载-位移曲线斜率出现明显拐点,如图10中A点所示。

2) 混凝土开裂至钢板开始屈服前阶段

腹板混凝土开裂后,构件刚度有所降低。在外包钢屈服前,荷载-挠度曲线大致呈直线,挠度增长速度较缓慢,梁的整体工作性能良好。此阶段可视为弱非线性受力阶段。

3) 钢板开始屈服至极限荷载阶段

试件SJ1的荷载达到0.57Fu(SJ2的荷载达到0.65Fu、SJ3的荷载达到0.55Fu)时(如图10中B点所示),外包钢的底板开始屈服。此后,荷载-挠度曲线开始偏离原来的直线,呈非线性变化。当荷载超过0.85Fu时,纯弯区段外包钢大部分已屈服,此时梁已进入塑性强化工作阶段。随着荷载的进一步增加,跨中挠度达到102 mm (1/50净跨)时,认为荷载达到极限荷载(图10中黑色竖虚线对应的单点加载值)。

4) 极限荷载后的阶段

当荷载超过极限荷载后,试件仍可继续变形,直至混凝土压碎。

2.3 沿梁截面高度方向的应变分布

图11为试件SJ1跨中截面沿高度方向的应变分布图。在受力初期(0.60Fu以前),应变沿试验梁截面高度呈线性变化,梁腹板和翼缘板的弯曲曲率基本相同,这说明梁在弹性阶段的截面应变分布基本上符合平截面假定。外包钢和混凝土翼缘板接触面上基本无相对滑移变形,外包钢和混凝土共同工作的情况良好,外包钢全部处于受拉区。

图11 试件SJ1跨中截面应变沿高度方向的分布模式Fig.11 Strain distribution along the height of the middle cross-section of the specimen SJ1

当荷载达到0.60Fu以上时,梁进入非线性受力阶段,可以看到距梁底230 mm高度处(混凝土翼缘板底部),外包钢应变与混凝土翼缘板应变产生了明显的应变差,表明外包钢和混凝土翼缘板接触面上出现了相对滑移变形。腹板和翼缘的弯曲曲率仍基本一致,腹板和翼缘分别符合各自的平截面假定,但梁全截面已不符合平截面假定。

随着荷载的进一步增加,外包钢和混凝土翼缘板接触面上的相对滑移变形发展速率变大,试验梁中和轴不断上移。梁翼缘板截面的应变分布仍大致呈直线,但腹板截面的应变分布已不再是直线,外包钢和混凝土的组合作用下降。

2.4 钢板与混凝土间的滑移特征与分布形式

图12为试件SJ3沿跨度方向的相对滑移分布图。由图12可知,新型组合梁的滑移具有以下特点:

(1) 外包钢屈服后,外包钢与混凝土之间开始出现明显的相对滑移;随着荷载的进一步增加,外包钢与混凝土的相对滑移量增长速率不断加大。

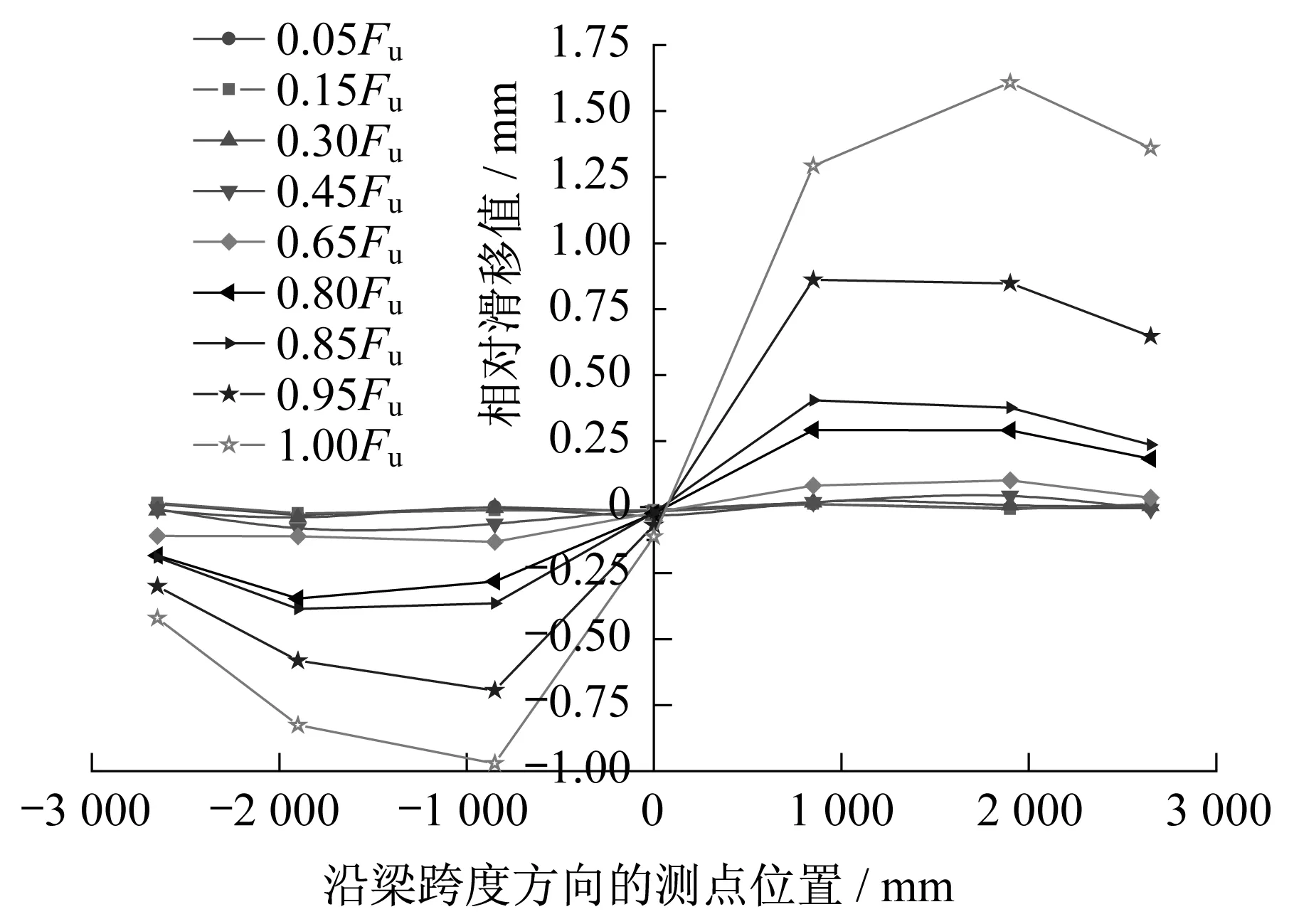
图12 试件SJ3沿梁跨度方向的相对滑移分布图Fig.12 Slip distribution between steel plate and concrete along the length of the specimen SJ3

(2) 外包钢和混凝土接触面的粘结应力有两类:一类是剪跨段中任意两截面处钢板的拉应力不相等,钢板产生的粘结应力;二类是梁腹板混凝土开裂后,裂缝间的钢板产生粘结应力。在极限荷载之前,滑移测点中的最大值位于加载处的测点,这是因为随着荷载的增加,纯弯段的混凝土受弯大量开裂,裂缝间的粘结应力逐渐退化和丧失,钢板与混凝土之间产生相对滑移,剪跨段由弯矩引起的滑移相比纯弯段更小,端部的滑移主要由跨中向端部传递产生,而剪跨区的栓钉有效抵抗了由试件中部向端部传递的部分滑移,所以,相对滑移最大值位于纯弯段的边界,即加载处测点。随着荷载的增加,由于应力重分布,剪跨段的栓钉承受的剪力逐渐达到极限承载力,最大滑移位置向梁端移动,但当荷载接近极限1.0Fu时,最大滑移出现在加载点与端部之间,并未出现在新型组合梁的端部,这是因为支座处由于反力的作用加强了抗滑移能力,有效抵抗了部分滑移。

(3) 在达到极限荷载时,试验梁外包钢与混凝土之间均产生了明显的滑移,最大滑移值大于1.6 mm。

(4) 外包钢屈服前,外包钢与混凝土间的相对滑移很小(小于0.05 mm),表明此时新型组合梁的外包钢和混凝土共同工作情况良好,在设计使用阶段,可以按不考虑滑移来进行计算分析。

(5) 新型组合梁即使是按完全抗剪连接设

计,外包钢与混凝土间的相对滑移仍不可避免。

2.5 试件试验结果分析

试件SJ1、SJ2、SJ3的主要试验结果见表4。由表4可知,混凝土压溃时纯弯区段外包钢基本全截面屈服,形成塑性铰,期间伴随裂缝的急剧开展和梁挠度的急剧增大,具有明显的破坏预兆,因此,即使外包钢与混凝土接触面发生了相对滑移,仍可以认为试件未发生整体剪切破坏,而发生正截面受弯破坏,属于延性破坏类型。可将外包钢屈服荷载作为正常使用阶段验算最大变形的依据,此时平均挠度为l0/234(l0/为试件净跨),小于《混凝土结构设计规范》(GB 50010—2010)[22]规定的挠度限值l0/250。强屈比Fu/Fy大于1.54,位移延性系数δu/δy大于4.16,表明新型组合梁具有较高的安全储备和良好的延性。

表4试件主要试验结果

Table 4The main experimental results of specimens

3 有限元分析

3.1 有限元模型

本文以试验试件为研究对象,采用通用有限元分析软件ABAQUS建立与之相对应的有限元模型,模拟构件加载的全过程和受弯破坏形态下构件的受力性能。模型各组成部分单元类型均选择一次积分单元,混凝土采用实体单元C3D8R,外包钢采用壳单元S4R,钢筋采用桁架单元T3D2,通过Embedded方式嵌入混凝土中,栓钉采用非线性弹簧单元spring2。为避免应力集中造成有限元模型收敛困难,在支座和加载位置处建立弹性钢垫块和分配梁,其采用实体单元C3D8R。

3.2 材料的本构关系

3.2.1混凝土

本文有限元模型采用混凝土塑性损伤模型模拟混凝土材料,该模型假设的两种主要破坏方式为混凝土受拉开裂和受压压溃,采用Drucker-Prager准则作为判定混凝土破坏条件。混凝土的应力应变关系采用的是《混凝土结构设计规范》(GB 50010—2010)[22]中的应力-应变关系曲线,混凝土受拉和受压的应力-应变曲线计算公式分别如式(1)和式(2)所示。

σ=(1-dt)Ecε

(1)

σ=(1-dc)Ecε

(2)

式中:dt为混凝土单轴受拉损伤演化参数;dc为混凝土单轴受压损伤演化参数,按《混凝土设计规范》(GB 50010—2010)[22]相关规定取值;Ec为混凝土的弹性模量。

3.2.2钢材

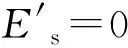
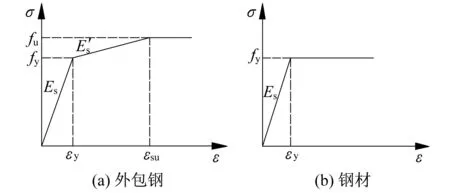
图13 钢材应力-应变本构关系曲线图Fig.13 The stress-strain curve of steel

3.2.3栓钉

栓钉的纵向剪力-滑移曲线采用Ollgaard[23]提出的栓钉剪力-滑移模型,其剪力滑移公式如式(3)所示。本文有限元模型中栓钉的极限抗剪承载力公式采用《钢结构设计规范》(GB 50017—2003)[20]的规定,如式(4)所示。

(3)

(4)

对于栓钉的极限滑移能力,本文采用Ollgaard[23]提出的极限滑移公式,计算式如下:

Sf=(0.45-0.002 1fc)×ds

(5)

式中:Sf为栓钉的极限滑移值;ds为栓钉的栓杆直径。

栓钉沿垂直于钢板方向的本构关系决定了栓钉的抗掀起性能,本文采用ABAQUS中的双线性强化模型模拟栓钉的抗掀起作用,其中强化阶段斜率取弹性模量的1%,达到极限应变后曲线的斜率为零。

3.3 接触作用

混凝土与外包钢的接触作用考虑法向及切向两个方向的定义。混凝土与外包钢接触面法线方向的接触为“硬”接触,切向方向的接触模型用罚函数摩擦模型来描述,混凝土与外包钢的接触面的摩擦系数取为0.1。混凝土与分配梁、外包钢与钢垫块的接触关系采用绑定(Tie)的方式来模拟。

3.4 几何模型

几何模型按照试件的实际尺寸建立,由于试验构件具有几何对称和加载方式对称的特点,本文有限元分析中的所有模型均采用1/4结构模型,以提高计算效率。在纵向和横向对称面上施加对称约束。通过计算分析,本文有限元模型的网格尺寸大小既能保证计算结果精度,又能把计算时间控制在可接受的范围内,模型的网格尺寸如图14所示。

图14 经网格划分后的有限元模型Fig.14 The finite element model after meshing

3.5 失效准则

本文有限元模型有两种失效模式:一种是在外包钢和混凝土接触面之间的抗剪承载力足够的前提下,混凝土达到极限压应变或钢材达到极限拉应变,即可认为模型发生正截面弯曲破坏;另一种是混凝土与外包钢之间的抗剪连接件数量较少时,二者之间发生较大相对滑移,在混凝土达到极限压应变或钢材达到极限拉应变之前,栓钉达到极限滑移值,即可认为模型发生纵向滑移破坏。

3.6 数值模拟结果与试验结果对比

3.6.1荷载-挠度曲线

图15为试验结果与数值模拟结果的荷载-跨中挠度曲线对比图。从图15中可以看出,试验结果与数值模拟结果的荷载-跨中挠度曲线变化趋势相似,即两者的刚度变化较为一致。

图15 试验结果与数值模拟结果的对比Fig.15 Comparison of experimental results and numerical simulation result

3.6.2特征荷载值及其对应挠度

表5为新型组合梁特征荷载值及其对应挠度值的试验平均结果与数值模拟结果的对比。从表5中可以看出,试验平均结果与数值模拟结果十分接近,两者的误差在9%以内。

表5特征荷载值及其对应挠度对比

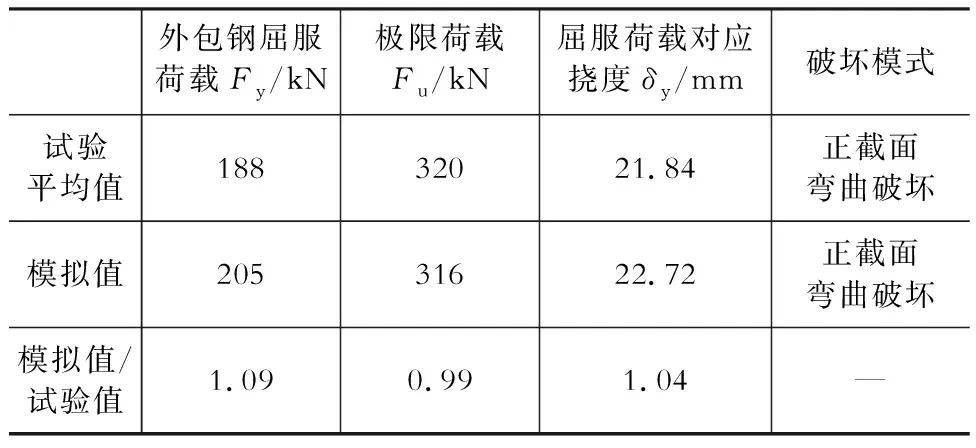
Table 5Comparison of characteristic load values and their corresponding deflection

3.6.3应力、应变云图

图16为极限状态下外包钢的Mises应力云图,从图16可以看出,极限状态下处于纯弯段位置的外包钢基本屈服。

图16 极限状态下外包钢的mises应力云图Fig.16 Mises stress nephrogram of encased steel in the limit state

图17为极限状态下混凝土的沿梁纵向应变云图,从图17可以看出,极限状态下混凝土翼缘板顶部的极限压应变达到0.003 3,表明混凝土已压碎。由此可以判断有限元模型的破坏形式为正截面弯曲破坏,即跨中外包钢基本屈服后,受压区边缘混凝土压碎,与试验结果一致。

图17 极限状态下混凝土的纵向应变云图Fig.17 Longitudinal strain nephrogram of concrete in the limit state

通过以上数值模拟结果与试验结果的对比,可以验证本文有限元建模分析方法较为合理,结果准确可信。

3.7 参数分析

3.7.1腹板混凝土的影响

为研究腹板混凝土对新型组合梁静力性能的影响,本文以试验试件为原始模型,在此基础上分别建立腹板内填充混凝土和不填充混凝土的数值模型如图18所示。

图18 有限元模型截面示意图Fig.18 Schematic section of the finite element model

图19为计算得到的有无腹板混凝土下的荷载-跨中挠度曲线,由图19可知,腹板混凝土的有无对新型组合梁的刚度基本没有影响,但对极限承载力有较大影响,有腹板混凝土的新型组合梁比无腹板混凝土的新型组合梁承载力提高了20%左右,这是由于外包钢与混凝土的接触面积较大,界面粘结力较高,使得腹板混凝土在外包钢的约束作用下能承受部分拉力,这也是新型组合梁的抗弯承载力高于普通钢-混凝土组合梁的原因之一。

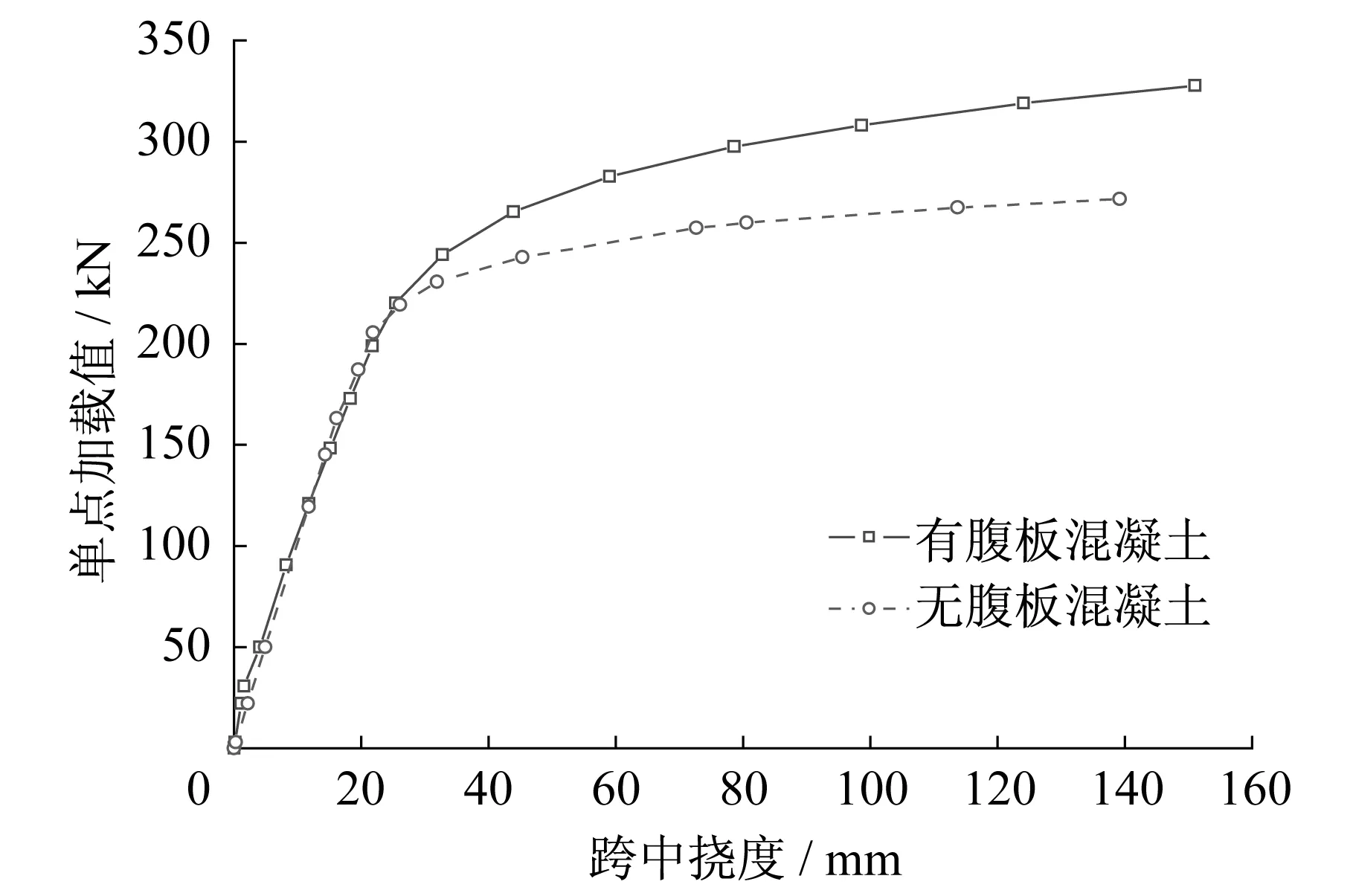
图19 有无腹板混凝土下的荷载-挠度曲线Fig.19 Load deflection curves of beams with and without concrete web

3.7.2栓钉间距的影响

为研究不同栓钉间距对新型组合梁性能的影响,本文以试验试件为原始模型,在此基础上通过改变栓钉间距参数来得到不同剪力连接系数的模型。建立了9种不同栓钉间距的数值模型,栓钉间距分别为0 mm (外包钢与混凝土接触面绑定约束,即不考虑界面滑移)、150 mm、200 mm、250 mm、300 mm、400 mm、500 mm、600 mm。

图20为计算得到的不同栓钉间距下的荷载-跨中挠度曲线。从图20中可以看出,栓钉间距对新型组合梁的性能有着显著影响,栓钉间距越大,新型组合梁的刚度和极限承载力越小;当栓钉间距在0～250 mm范围内,增大栓钉间距可增加构件延性,但其极限承载力的变化幅度不大;当栓钉间距大于300 mm时,由于外包钢与混凝土之间的抗剪承载力过低,新型组合梁的破坏模式由正截面弯曲破坏转化为纵向滑移破坏。

图20 不同栓钉间距下的荷载-挠度曲线Fig.20 Load deflection curves of beams with different stud spacing

4 结 论

本文对3根足尺外包冷弯U形钢-混凝土T形组合梁进行了受弯性能试验;对试验过程及试验现象进行了分析,获得了试件的荷载-挠度曲线、应变沿梁截面高度的分布模式、钢板与混凝土间的滑移分布、破坏形态等受力特性与变形特点,并用有限元软件进行了模拟,得到了准确可靠的有限元模型,在此基础上研究得到了腹板混凝土和栓钉间距对新型组合梁性能的影响特征与变化规律,得到了以下结论:

(1) 新型组合梁的破坏形态为正截面弯曲受压破坏,外包钢未发生明显鼓曲及掀起变形,且满足正常使用阶段挠度限值的要求,强屈比Fu/Fy大于1.54,位移延性系数δu/δy大于4.16,具有较高的安全储备、良好的延性和经济性。

(2) 新型组合梁充分发挥了两种材料的性能,外包钢内填充的混凝土,对钢板产生了约束作用,避免了钢板的局部屈曲,提高了组合梁的抗弯刚度。

(3) 在外包钢开始屈服以前,截面应变分布基本上符合平截面假定,外包钢与混凝土的共同工作能力良好,在设计使用阶段可以按不考虑滑移计算。但外包钢开始屈服后,外包钢与混凝土发生了较明显的相对滑移,截面应变分布不再符合平截面假定。

(4) 在达到屈服荷载后,外包钢与混凝土之间开始出现明显的相对滑移。在达到极限荷载时,最大滑移位移出现在加载点与端部之间,且最大滑移量在1.6 mm左右。

(5) 通过有限元数值分析结果与试验结果对比可知,两者特征荷载值及其对应挠度值十分接近,误差不超过9%,且数值分析获得的荷载-位移曲线与实测曲线吻合较好,证明本文有限元建模分析方法较为合理,结果准确可信。

(6) 腹板混凝土的有无对新型组合梁的刚度基本没有影响,但对极限承载力有较大影响,有腹板混凝土的新型组合梁比无腹板混凝土的新型组合梁承载力提高了20%左右。

(7) 随着栓钉间距的增大,刚度和极限承载力均减小,组合梁的破坏模式由正截面弯曲破坏转为纵向滑移破坏。