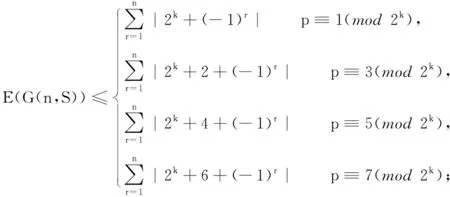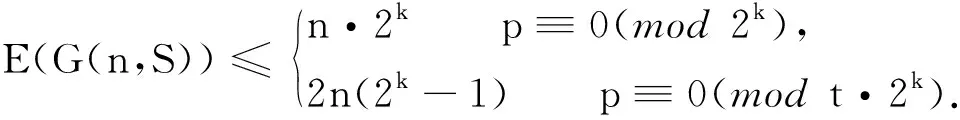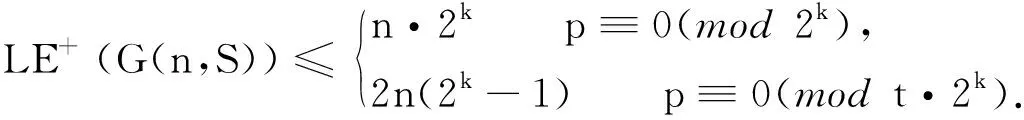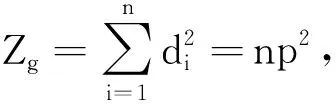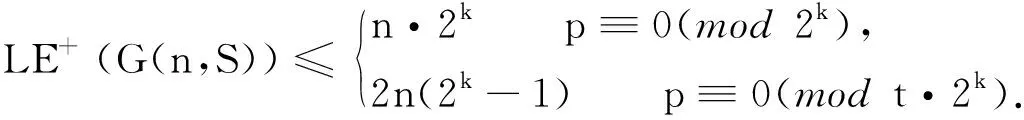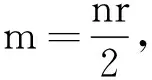循环图的无符号Laplacian能量的上界*
2018-09-12徐幼专
徐幼专
(邵阳广播电视大学,湖南 邵阳 422000)
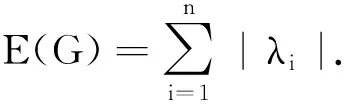
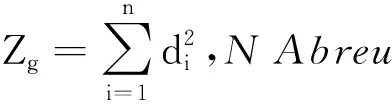
若G是一个具有n个顶点和m条边的简单连通图,则
(1)
等式成立当且仅当G是一个正则图;
(2)
等式成立当且仅当G是一个空图或是一条边加n-2个孤立点所构成的图.
K C Das等[12]证明了如下结论:设G是一个具有n个顶点、m条边和秩为r的简单连通图,则
称一个图为循环图,若它的邻接矩阵是一个循环矩阵,即它是循环群上的Cayley图.循环图是一类重要的互联网络拓扑图,循环网络是双环网的自然推广.循环图具有较好的稳定性、高对称性和可扩展性,在过去的几十年里,循环图不断地出现在编码理论、VLSI设计、Ramsey理论、并行计算和分布式计算中.
设n为正整数,给出集合{0,1,2,…,n-1}的一个子集S(又称符号集),即S⊆{0,1,2,…,n-1},0∉S.具有n个顶点的循环图记为G(n,S),如果它的任意2个顶点i与j相邻当且仅当i-jmodn∈S.假设S={n1,n2,…,np},ni∈{1,2,…,n-1},则G(n,S)是一个度为p的正则图.
引理1[13]若G(n,S)是一个具有n个顶点的循环图,
S={n1,n2,…,np}n1 则 (ⅰ)当p为奇数时,循环图的能量 (ⅱ)当p为偶数时,循环图的能量 引理2[14]若G是一个具有n(n≥2)个顶点和m(m≥1)条边的简单图,则 其中 定理1若G(n,S)是一个具有n个顶点的循环图, S={n1,n2,…,np}n1 则 (ⅰ)当p为奇数时,循环图的无符号Laplacian能量 (ⅱ)当p为偶数时,循环图的能量 根据引理1,当p为奇数时, 结合(1)式有 当p为偶数时,结合(1)式有 定理2若G(n,S)是一个具有n个顶点的r-循环图,则LE+(G(n,S))≤2r(n-1). 定理3若G(n,S)是一个具有n个顶点的r-循环图,则 其中 根据引理2,定理3显然成立,证明略去. 仍以循环图G(12,S),S={1,6,11}为例,利用定理3可得LE+(G(12,S))≤47.76,结果与软件计算结果相符.