基于正交试验的机车风源系统供风能力参数研究
2018-09-12张长东
张长东, 魏 伟
(1 中国铁路广州局集团有限公司, 广州 511483;2 大连交通大学 交通运输工程学院, 辽宁大连 116028)
随着国民经济的发展,人们生活水平的提高,人们对出行的安全性和舒适度提出了更高的要求。为了满足人们的要求,中国铁路总公司对客运列车进行了多次改造。空气制动系统、机车鸣笛,车辆空气弹簧、塞拉门、集便器等各种用风设施的大量使用,大幅提升乘坐舒适度。这些用风设施的使用给机车供风能力提出了更高的要求,特别是在用风设施集中使用时间内,即睡觉前后旅客洗漱上厕所集中的时间以及列车在通过曲线和坡道等复杂工况时,用风量大大增加。但是,机车风源系统的设计参数多年来基本没有改变,部分机车在实际运用中出现了供风能力不足,压缩机频繁启动的现象。这些现象导致压缩机工作率低,易造成润滑油乳化,使压缩机泵风作用减弱,严重影响用风设施的正常使用以及其功能的正常发挥,甚至影响列车运行控制能力。同时,压缩机频繁启动也缩短了压缩机的使用寿命。因此,如何保证机车风源系统供风能力,使客运列车用风量与机车风源系统供风能力达到最佳匹配,对客运列车的行车安全具有重要意义。
国内对机车供风系统的研究较少,文献[1]提出的机车风源系统参数选择流量法为机车风源系统的设计提供了有效手段。文献[2]通过对城轨车辆供风系统用风量估算,计算出风源系统的充风时间,根据现场试验验证供风系统设计是否满足要求。文献[3]介绍了影响机车风源系统供风能力的压缩机型式、排气压强、总风缸压强选取原则、空气压缩机排气量和主风缸容积的计算与选择方法。文献[4]对解决客运机车与客车空气系统匹配问题进行了探讨,提出用两个空气压强控制开关分别控制两台压缩机,且两台压缩机启动压强保持一定差值;或将制动用风和辅助用风系统分离设计。文献[5]介绍了动车组风源系统的组成、功能、参数,同时还介绍了风源系统的管理模式。文献[6]对高速动车组制动供风系统进行了仿真与分析。文献[7]对北京地铁1号线地铁列车风源系统出现的HS20型空气压缩机频繁启动进行了分析,指出通过增加安装压强继电器和细化控制压强仍不能有效解决压缩机频繁启动的问题。文献[8]分析了压缩机排气量、机车总风缸容积及列车制动系统的泄漏对列车充气时间的影响,指出了机车供风能力与机车制动系统中继阀的关系。上述对机车风源系统的研究主要以质量守恒为依据,仅考虑稳态特性,也没有明确提出机车风源系统各参数之间的关系及对压缩机启动次数的影响显著性。因此,在保证机车供风能力前提下,如何优化机车风源系统参数,解决压缩机频繁启动的现象迫在眉睫。
首先建立了列车风源及用风系统模型,开发了对应的基于气体流动理论的仿真程序。根据试验结果确定客运列车的用风量。在保证用风量的前提下,通过调整主风缸容积、压缩机开启压强、压缩机排气量,深入分析机车风源系统参数变化对其供风能力的影响。基于正交试验法,通过正交试验分析得到最优解,为实际运用中机车风源系统参数设计提供理论依据。
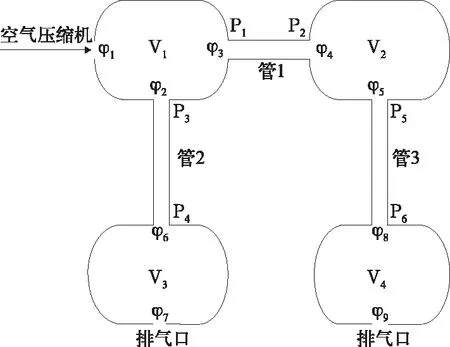
图1 列车风源与用风系统模型简图
1 列车风源与用风系统模型
机车风源系统由两台压缩机和两个主风缸组成,两台压缩机与主风缸1相连,两个主风缸间通过管路相连。主风缸1主要给列车制动系统供风,主风缸2负责列车中各车辆空气弹簧、塞拉门、集便器等用风设施的供风。上述供风系统根据实际情况每个压缩机模型化为一个具有固定质量流率的恒流源,一个主风缸模型化为一个压力容器。
在用风系统中,每个车辆的塞拉门、空气弹簧、集便器,制动系统都独立用风,并且每个车辆的用风具有不同时性和不同量性,因此对每个车辆用风独立模型化难度较大,同时也没有这个必要,因为对应于风源系统,主要考察的是所有用风装置用风总量,因此用风系统集成模型更加实用化,为此将列车用风假定为两个大容量压力容器,一个压力容器主要代表制动系统,另一个压力容器代表其他用风。列车风源及用风系统共模型化为4个压力容器,两个压缩机,模型中还包含了各压力容器间的连接管。图中V1、V2是主风缸,V3、V4是用风装置。
将压缩机模型化为一个恒质量流率进气源,单位时间内进气量恒定,它开启时(可能两个压缩机同时开启,也可能一个开启,或者全部关闭,开启的控制方式由设定压强确定),有一个等质量流率的质量通过 孔流入主风缸V1。φ3、φ4孔是连接2个主风缸管的两端开口,此孔径开度大小是一个常量,(图1中的第一管,管两端编号为P1,P2)。φ2、φ5孔分别为两个主风缸与用风装置风缸连接管主风缸一侧的进排气孔径,此孔径开度为常量,并在此处设置限压阀。φ6和φ8分别是2个主风缸与用风装置风缸连接管用风装置风缸一侧进排气孔径,该孔在整个工作过程中面积不变化。V3是用风装置1的虚拟风缸,该风缸容积与列车中制动系统中列车管和副风缸容积总和相等,该用风装置有一个排气孔 ,通过调整该排气孔模拟制动装置用风量,V4为用风装置2的虚拟风缸,该风缸容积与空气弹簧、集便器等装置储风容积相等。在该用风装置中设置一个排气口φ9,用来模拟辅助用风系统用风情况。
根据气体动力学原理,编制了仿真气体流动程序,该仿真系统可以分析各缸容积、初压强,管路参数及初压强,各排气口参数、压缩机压缩量、开启关闭压强等各种参数影响,是选择主风缸容积、确定压缩机工作压强,各种部件用风量对系统压强影响的分析工具。
2 列车用风量的确定
机车用风量增加,压缩机工作率不高以及压缩机频繁启动的现象在很多铁路局出现,为此在某条线路上进行了列车压缩机工作状态试验。该试验测试了主风缸压强,压缩机工作个数以及压缩机工作时间,图2为某试验部分时间段的测试结果曲线,图中绘出了主风缸压强和压缩机工作情况。
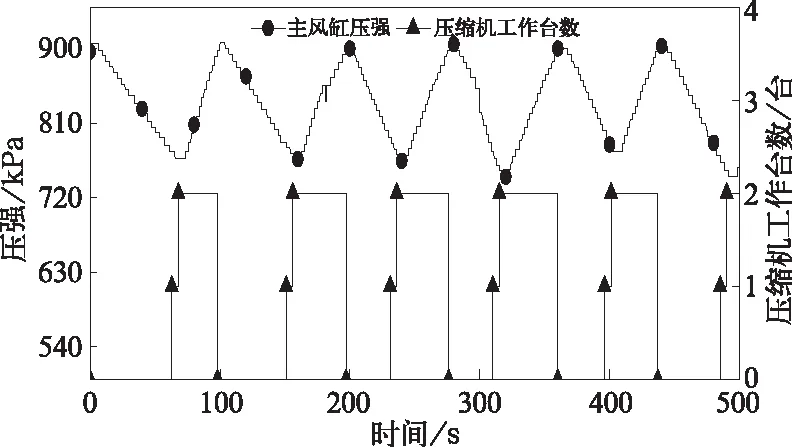
图2 主风缸压强及压缩机启动台数试验结果
由图2可见,当车辆用风后,主风缸压强下降。用风量大小决定主风缸压强的下降速率,当主风缸压强下降到约767 kPa时,一台压缩机开始启动,间隔5 s后另一台压缩机启动,两台压缩机启动时间差很小,可以认为两台压缩机同时启动,理论设定两台压缩机同时启动压强为750 kPa,显然压缩机启动实际值和理论值相差约17 kPa。当压缩机工作后,主风缸压强迅速上升,压强上升速率与压缩机压气能力直接相关,能力越大,压强曲线斜率越大,压强上升越快,当主风缸压强达到907 kPa时,压缩机停止工作。因为用风装置继续用风,压缩机不再给主风缸供气,主风缸压强再次出现下降,从主风缸压强下降速率看,第2次主风缸压强下降和第1次压强速率基本相同,即用风量基本一致,同样在主风缸压强下降到较低时,压缩机开始工作,主风缸压强再一次上升。在此段试验数据中主风缸压强下降6次,上升5次(对应压缩机工作)。表1为此段试验数据主风缸压强下降和上升速率表,从表中看出第4次下降斜率最大为4.5 kPa/s,说明该时间段内用风量最大,第1次下降斜率最小为2.3 kPa/s,说明该时间段内用风量最小,6次压强下降平均速率为3.4 kPa/s,而从主风缸压强上升速率可以看出压缩机进气量与用风量差异导致的压强上升。同时从图2压缩机工作个数看,此压缩机工作压强设定并不规范,仅在750 kPa左右设定双压缩机同时起作用,压缩机启动压强具有一定离散性,6次启动压强分别为767,766,764,745,775,745 kPa,平均双压缩机启动压强为760 kPa。

表1 主风缸压强下降和上升速率表 kPa/s
为了解决由于列车大用风量而产生的双压缩机启动压强偏高引起的压缩机频繁启动的问题,需要确定该条线路上列车最大用风量及所在时间段。由于用风量大小决定主风缸压强的下降斜率,可以近似认为主风缸压强的下降斜率就等于列车的用风量。图3为列车在该条线路上9点至23点的主风缸压强的下降斜率曲线,由图3可知列车在18点时,主风缸压强的下降斜率最大,斜率为3.5 kPa/s,即用风量最大,在17点时的主风缸压强的下降斜率仅次于18点,斜率为3.3 kPa/s。18点用风量达到最大值,故选取18点用风为最大用风条件。

图3 主风缸压强下降斜率试验曲线
2.1 机车充风能力校核
根据试验数据特征,使用仿真模型,仿真机车风源系统的充风与用风完整过程。首先确定压缩机进气量的准确性,为此,将模型中用风风缸容积设置为零,并控制仅有一个压缩机工作,以此实现一个压缩机向主风缸充气过程,并与同样条件的试验结果比较确定压缩机充气系数。图4是仿真和试验的压缩机给主风缸充气的压强变化曲线,从图中可以看出,一台压缩机向主风缸充气,主风缸压强由0 kPa上升至900 kPa试验所用时间为371 s,仿真所用时间为391 s,仿真曲线和试验曲线基本吻合,由此确定了压缩机充气系数。
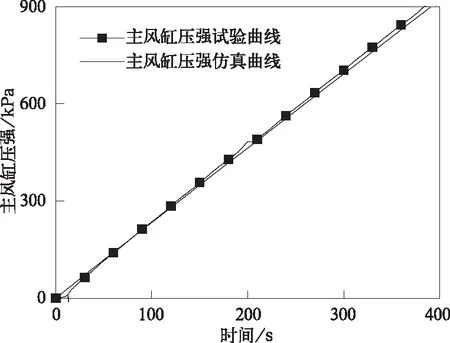
图4 主风缸初充气压强曲线
2.2 列车用风量确定
在压缩机充气能力确定后,根据试验结果设定压缩机启动压强,就可以仿真机车风源系统动态工作过程。在仿真过程中,不断调整用风装置的排气孔大小模拟列车中用风装置的用风量,同时再比较主风缸压强和压缩机工作台数。当主风缸压强变化曲线和试验曲线接近,同时压缩机工作情况也与试验结果相近时,就确定此时的用风装置排气量就是真实列车的用风量。为了排除仿真与试验对应的偶然性,共选取了18点的1 h的试验数据作为对比。根据该段试验数据压缩机平均开启压强为788 kPa,主风缸容积1 200 dm3,压缩机排气量2.4 m3/min,利用仿真程序,调整用风装置的排气孔大小,对该小时内主风缸压强和压缩机工作台数进行仿真,图5是该段时间试验与仿真的主风缸压强与压缩机工作台数随时间的变化曲线。由图可知,在一个小时内,压缩机共启动44次,每次启动几乎都是两台压缩机同时工作;压缩机工作时间试验值为1 672 s,占总时间的46.4%,压缩机工作时间仿真值为1 753 s,误差为4.87%。压缩机启动前和压缩机启动后主风缸压强变化斜率仿真结果和试验结果基本一致。由于试验测试结果中压缩机工作启动压强偏差,个别次数压缩机工作开始时间仿真值和试验值略有差异,试验结果中有某几次压缩机启动压强明显低,低于压缩机平均启动压强(仿真中设定的压缩机工作压强与平均启动压强相等),压缩机工作压强越低,压缩机启动时间越滞后。从总的趋势看主风缸压强曲线和压缩机工作时间、启动个数与试验值基本吻合。因此,此时的用风装置排气量就是真实列车的用风量。
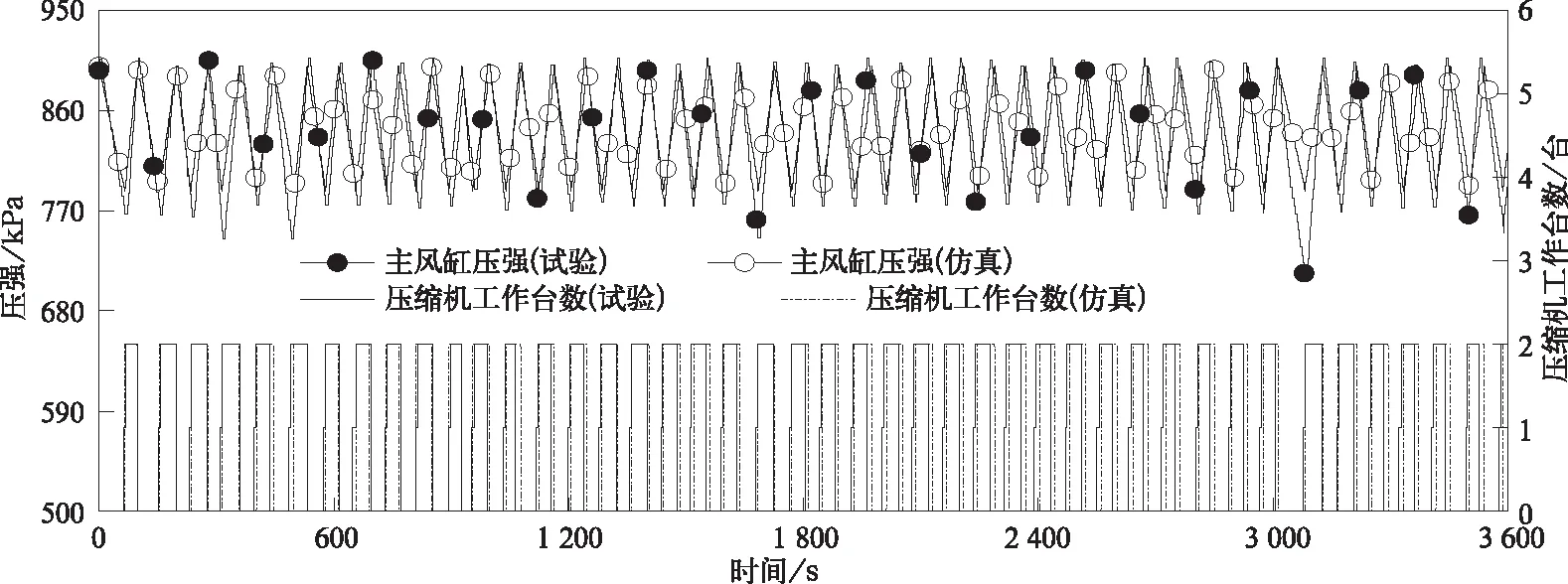
图5 主风缸压强及压缩机启动台数仿真与试验对比图
从18点时试验数据看出压缩机启动次数44次,大于30次/h,不满足压缩机工作要求,标准规定螺杆式压缩机应在额定工作压强、启停次数不超过每小时30次条件下,持续运行8 h后,各零部件不应损坏,无漏气、漏油现象[9];压缩机工作时间1 672 s,工作率为46.4%,且要求压缩机工作率越大越好。因此,需要对压缩机启动次数和压缩机工作时间进 行优化。为了使压缩机启动次数满足标准要求并确保压缩机工作率尽可能高,首先确定影响压缩机工作时间和工作次数的机车风源系统参数,分析这些参数变化对压缩机工作时间和工作次数的影响趋势,然后对压缩机工作时间和工作次数进行优化。
3 正交试验设计
主风缸容积、压缩机启动压强和压缩机排气能力都能够影响机车系统供风能力,多种影响因素多水平的优化最合理的方法就是正交试验法[10],下面使用正交试验方法分析参数影响并优选结果。
首先选取主风缸容积A、压缩机启动压强B和压缩机排气量C作为影响因子,压缩机工作时间Y1和压缩机启动次数Y2为检验指标,分别赋予3个参数两个水平,即主风缸容积1 200,1 300 dm3、压缩机双机启动压强750,740 kPa、压缩机排气量2.4,2.3 m3/min,利用L8(27)正交表[11]安排正交试验方案,见表2,共安排了8次试验,试验号1~8,A×B为因子A和因子B的交互作用,A×C为因子A和因子C的交互作用,B×C为因子B和因子C的交互作用。把影响因子主风缸容积A安排在L8(27)的第1列,压缩机启动压强B安排在L8(27)的第2列,压缩机排气量C安排在L8(27)的第4列,因子间交互作用A×B、A×C、B×C分别安排在L8(27)的第3、5、6列,第7列为空列,作为试验误差估计。K1为每一因子第一水平的检验指标试验结果之和,K2为每一因子第二水平的检验指标试验结果之和,为了计算方便,把检验指标Y1减去1 900,不影响分析的结论。极差R为K1、K2中最大值减去最小值即R=|K1-K2|,根据极差R的大小可以判断各因子对检验指标的影响大小,极差越大说明因子对检验指标的影响越大,反之,极差越小说明因子对检验指标的影响越小。由表2可知,对于检验指标压缩机工作时间来说,第4列的极差为343.6,是所有极差中最大的,对应的影响因子为压缩机排气量C,表明C因子对压缩机工作时间的影响是最主要的,其次是B×C、再其次是B、A×C、A×B、A,故因子及因子之间交互作用的主次关系为C>B×C>B>A×C>A×B>A,同理,对于检验指标压缩机启动次数来说,第1列极差最大为12,对应的影响因子为主风缸容积A,表明A因子对压缩机启动次数的影响最主要,第2列与第4列极差都为10,说明两个因子对压缩机启动次数的影响是相等的。故因子及因子之间交互作用的主次关系为A>B与C>B×C>A×B与A×C。
表2中压缩机启动次数均大于30次/h,且逐渐减小。4号试验压缩机工作时间最长为2 019.8 s,3号试验压缩机工作时间最短为1 924.0 s,两次试验压缩机工作时间相差仅为95.8 s,可见在这8次试验中压缩机工作时间虽有变化,但波动不大。在第8号试验条件下,即主风缸容积为1 300 dm3,压缩机双机开启压强为740 kPa,压缩机排气量为2.3 m3/min时,压缩机启动次数最小为31次/h,但仍不满足压缩机启动次数不大于30次/h的要求,故需继续进行正交试验。根据参数可供选择范围,主风缸容积1 200 L,压缩机双机开启压强680~760 kPa,压缩机排气量2.0~2.9 m3/min,进行多轮正交试验,正交试验优化结果如图6。
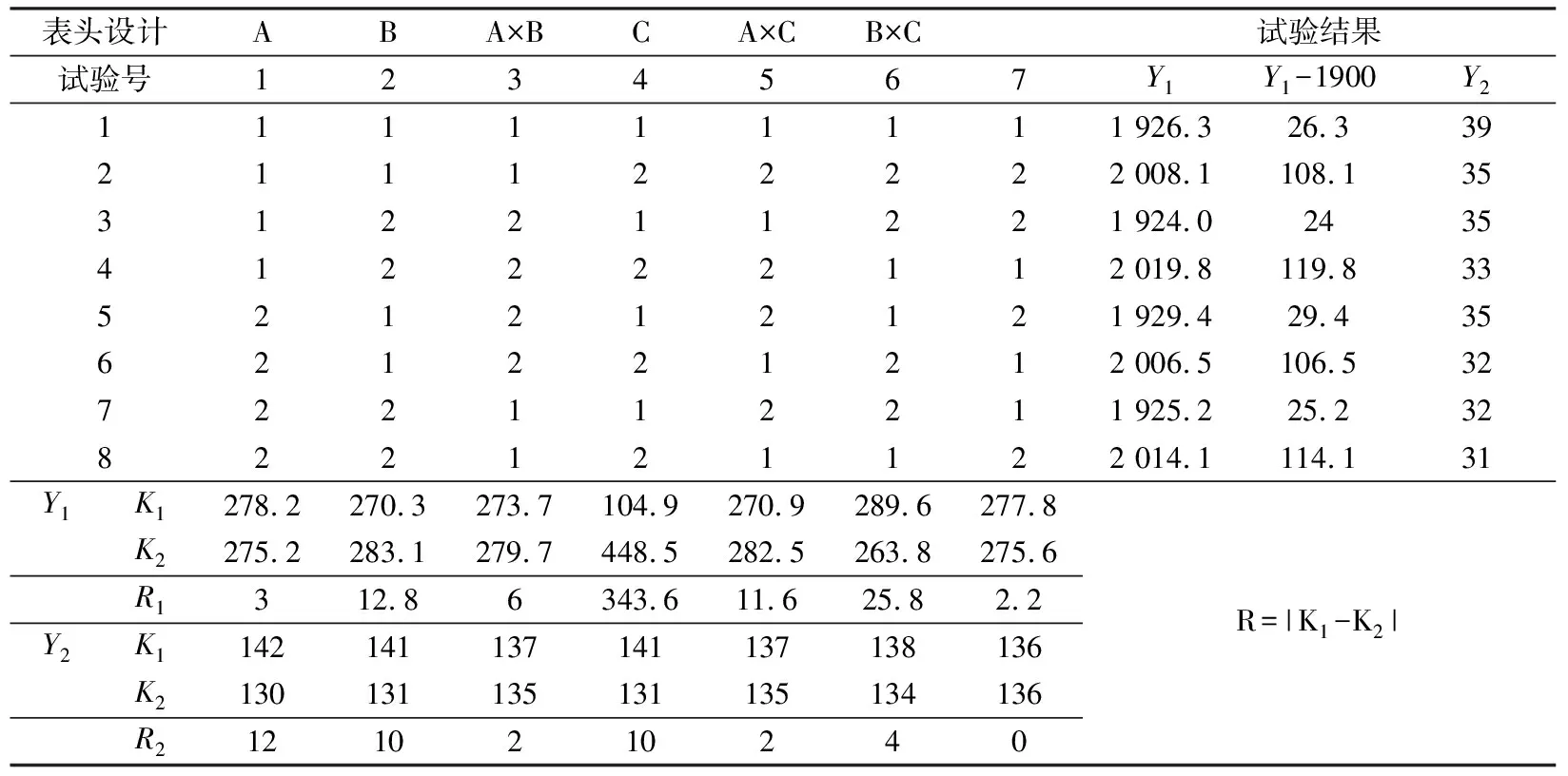
表2 正交试验方案及试验结果
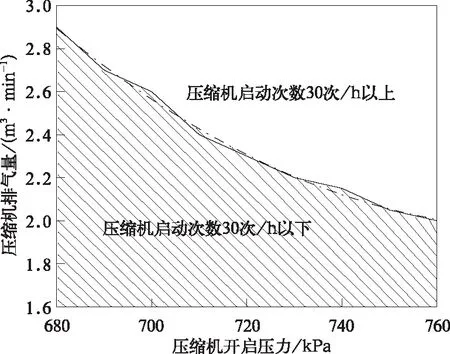
图6 压缩机排气量随压缩机开启压强变化
由图可知,当主风缸容积一定且压缩机实际控制方式为双机启动,在压缩机启动次数满足30次/h的情况下,压缩机双机开启压强与压缩机排气量成反比。压缩机双机开启压强越高,压缩机排气量许用空间越小,反之,压缩机双机开启压强越低,压缩机排气量许用空间越大。对曲线进行拟合,拟合公式为:
y=8.929×10-5x2-0.14x+56.573
(1)
其中x为压缩机双机开启压强;y为压缩机排气量。
因此,当主风缸容积一定且压缩机控制方式为双机启动时,要确定压缩机双机开启压强就可以由公式确定满足压缩机启动次数的压缩机排气量。
4 结 论
建立基于气体流动理论的机车风源及用风系统模型,首先根据试验数据确定列车用风量,在此基础上,基于正交试验法,分析参数影响,并通过仿真结果正交试验分析得到满足压缩机启动次数的主风缸容积、压缩机双机开启压强、压缩机排气量优化范围,为实际运用中机车风源系统参数设计提供理论依据。
(1)对压缩机工作时间的影响因素从大到小的顺序为:压缩机排气量,压缩机开启压强,主风缸容积。
(2)对压缩机启动次数的影响因素从大到小顺序为:主风缸容积,压缩机开启压强和压缩机排气量。
(3)当主风缸容积一定且压缩机控制方式为双机启动时,在压缩机启动次数满足30次/h的情况下,压缩机双机开启压强与压缩机排气量成反比。
(4)当主风缸容积一定且压缩机控制方式为双机启动时,得到了满足压缩机启动次数相对应的压缩机排气量和启动压力关系表达式。
