网格絮凝池结构参数对流场影响的数值模拟

刘 存，王庆涛，陈翔宇，姚娟娟, 张 智

(重庆大学 城市建设与环境工程学院， 重庆 400045)

1 研究背景

网格絮凝池是净水厂的关键构筑物之一，其絮凝效果直接影响后段沉淀过滤工艺的处理效率。随着计算机技术的高速发展，数值模拟方法成为网格絮凝池的重要研究手段[1-2]。易中慎[3]利用fluent对网格絮凝池中的入口流速、网格孔眼尺寸、栅板间距对网格絮凝池流场分布的影响进行了探讨，得出合理的栅板间距为600～700 mm；方千里等[4]对圆形孔眼网格板、不同圆形孔眼直径及距离进行了比较，得出圆形孔眼优于传统正方形孔眼以及圆形孔眼网格板的最优半径及网格板最优间距；王永威[5]通过不同栅条板间距、栅条间距、过水孔洞位置的数值模拟，确定了栅条絮凝池最佳水力条件；仲崇军[6]提出了絮凝评价指标湍动能k、有效能耗和涡旋速度梯度G′；李国强[7]确定了单层、双层栅条板间最佳间距；柳溪[8]对栅条絮凝池的尺寸、层间距进行了优化。这些研究主要涉及了网格孔眼尺寸、栅板间距、栅条间距等对流场分布的影响，对进口至首层栅条间的高度、宽深比暂无涉及。结合网格絮凝池内最低Re>100 000的工况条件，以及网格絮凝池数值模拟的众多研究现状，本研究采用适用于高Re数的湍流模型——标准k-ε湍流模型[9-11]，通过改变进口至首层栅条间的距离和池宽，探求达到最优絮凝水力条件的竖井结构参数，以期为网格絮凝池的设计提供一定的理论依据。

2 数学模型

2.1 几何模型

本研究对网格絮凝池进行简化模拟，取其中单个竖井作为研究对象。考虑到多层栅条的交叉布置，简化模型须表征三个维度的速度分布，因此采用三维模型来进行模拟计算，网格絮凝池几何尺寸如表1所示，三维模型示意见图1。

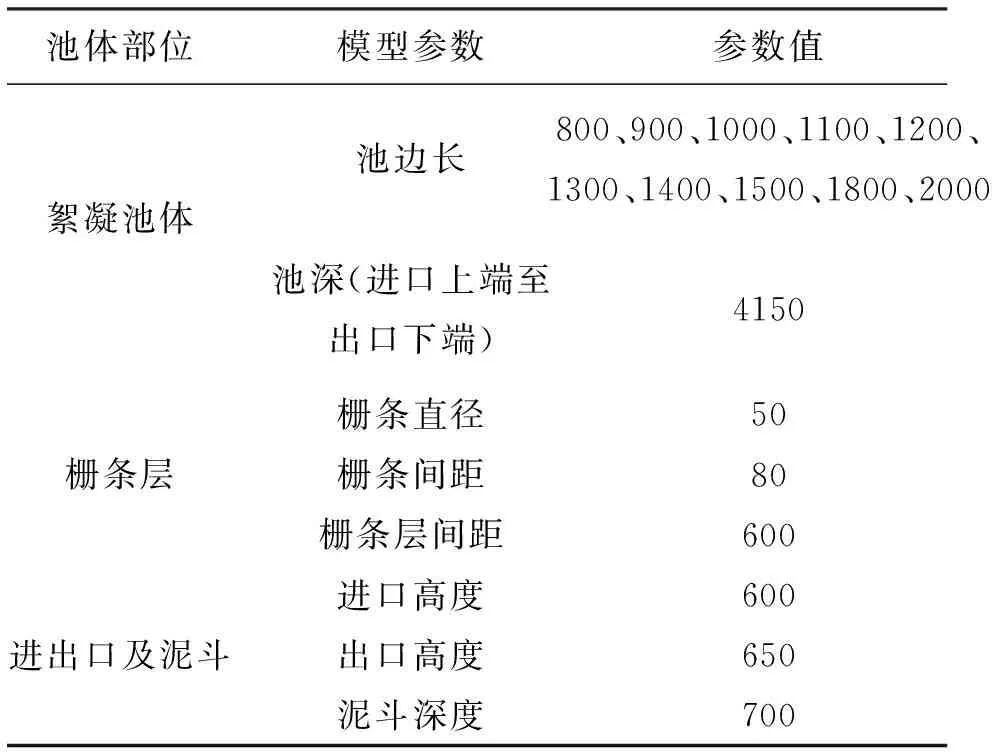
表1 网格絮凝池模型参数 mm

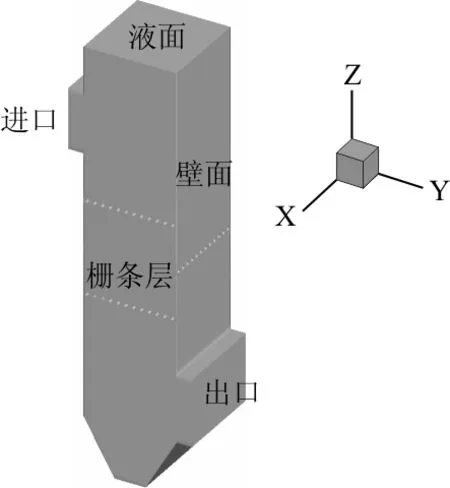
图1 网格絮凝池三维模型图

2.2 边界条件和求解方法

(1)进口边界条件：为保证网格絮凝池内流速满足《室外排水设计规范》GB 50014-2006(2014年版)的要求，入口设为速度进口velocity-inlet：v=0.2 m/s，采用Intensity and Hydraulic Diameter方法，其中湍流强度Intensity设为I=5%；

(2)出口边界条件:设为自由出流outflow；

(3)壁面边界条件：采用标准壁面函数法，流体材料选择water-liquid；

(4)使用压力与速度耦合的PIOS算法进行动态模拟，其中湍动能、湍动能耗散率和动量均采用二阶迎风格式。

2.3 网格无关性验证

数值模拟要保证其结果的可靠性，首先需要进行模型自验证。网格无关性验证是对网格疏密程度能否准确得出模拟结果的校核，网格稀疏、数量少会导致流场的模拟结果与实际工况产生不可接受的数据偏差。本文使用前处理软件ICEM CFD生成结构网格用于计算，网格节点数依据栅条的网格边界层数划分为6个梯度，进行网格无关性验证，网格参数详见表2。

表2 网格参数表

选取截面z=2.5 m上均匀分布的3个点——点1(0.3,0.8,2.5)、点2(0.6,0.8,2.5)和点3(0.6,1.0,2.5)作为监测点，读取3个监测点的速度值，做出其随网格数量变化的曲线，结果如图2所示。

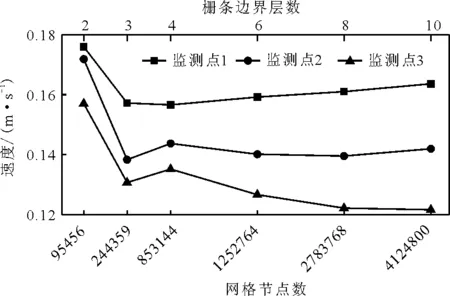
图2 网格无关性验证结果图

从图2中可以看出，当栅条的网格边界层数从2层增加到10层时，随着边界层数的增加，各监测点的速度值波动幅度逐步变小，模拟流场趋于稳定。结果表明，栅条网格边界层数达到6层，即网格节点数在125×104左右时，计算结果可靠，满足网格无关性要求。另外，模拟结果显示，流动可简化为定常流，故不进行瞬态计算及由瞬态计算产生的时间步长独立性验证。

3 模型的试验验证

为进一步查验数值模型的可靠性，采取试验手段进行辅助验证。以栅条最佳层数作为验证目标，设计试验模型共计6个竖井，前段两个竖井有4层栅条，中段两个竖井有3层栅条，末段无栅条。根据相似准则原理，以弗劳德数相等[12]得模型比尺为17.4，实物模型如图3所示。

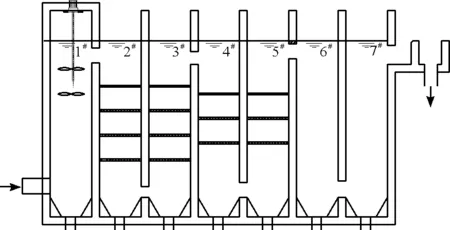
图3 网格絮凝池结构平面图和剖面图

试验采用脉冲示踪法测量模型的水力停留时间分布(RTD)[13-14]。以KCl为示踪剂，在模型入口端一次性投加100 mL饱和KCl溶液，随后在出口端用在线电导率仪监测其电导率变化，为方便与模拟结果对比，将测得的电导率换算成相应的质量分数，得出模拟与试验结果的RTD曲线对比图[15]，如图4所示。

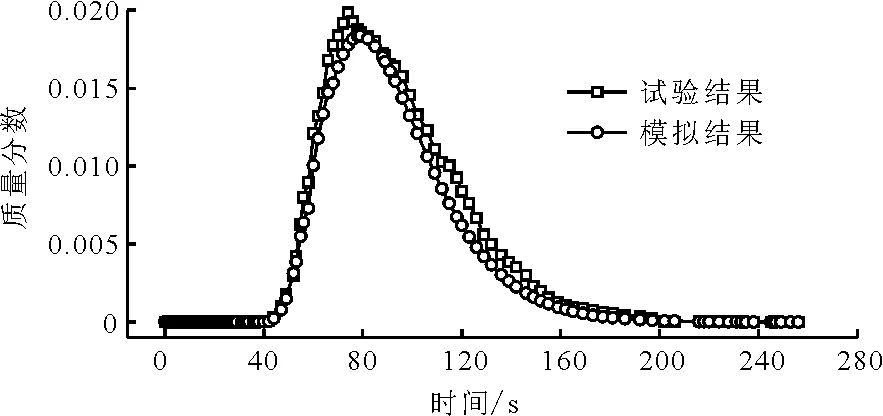
图4 质量分数-时间曲线图

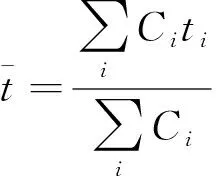
4 模拟结果与分析

4.1 进口到首层栅条距离对流场分布的影响

进口到首层栅条距离的不同必然在其流场初始段产生不同的水力条件，从而间接地对整个流场产生影响，良好的水力条件能够提供较大的速度梯度和大量的微涡旋，促进絮凝过程的高效进行。为此，下文探讨进口到首层栅条的距离按照表3变化时，网格絮凝池单个竖井流场的分布情况，流场的速度分布见图5。

表3 进口底部到首层栅条的距离(h1)

由图5可知， 随着h1距离的不断增大，竖井顶部死水区范围逐渐缩小，有利于提高竖井内整体的絮凝效率。当h1为0、200 mm时，首层栅条的扰流作用未充分发挥，导致靠近进口一侧的下部壁面产生了明显的死水区；当h1从400 mm增加至1 000 mm时，进口下部无明显死水区，且絮凝池主反应区流态均匀；当h1为1 200 mm时，靠近进口一侧壁面重新出现范围较大的死水区，降低了栅条的扰流效率。絮凝池内存在死水区时，产生的漩涡尺度较大，旋转半径较长，从而离心作用越弱，涡旋速度梯度越小。因此，从速度分布云图分析，h1在400～1 000 mm变化时，产生小尺度涡漩，从而产生较强的离心作用，涡旋速度梯度较大，此时的水利条件适宜絮体的快速增长。

在诸多研究中，已有学者开始将流场速度分布均匀性作为一个评价指标[16]。通过引入相对标准偏差(CV值)来量化流场速度分布的均匀性，从而对流场速度分布的均匀性的优劣做出评价。本研究中速度CV值通过如下公式计算得出：

(1)

(2)

虽然不同的方案中模型的网格节点数不同，但是模型的整体尺寸和网格参数一致，所以各模型中的采样点都采用统一的标准10×10，共计100个采样点。采样点位置在首层与中间层栅条中间，如图6所示，用以量化截面上速度分布的情况。根据采样点数据绘制流场速度分布图，见图7和8，并辅以湍动能云图(图9)与湍动能耗散率云图(图10)分析h1对流场分布的影响。

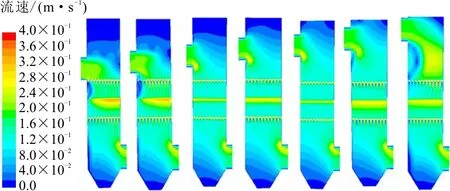
图5 x=0.45 m的各组截面速度分布云图

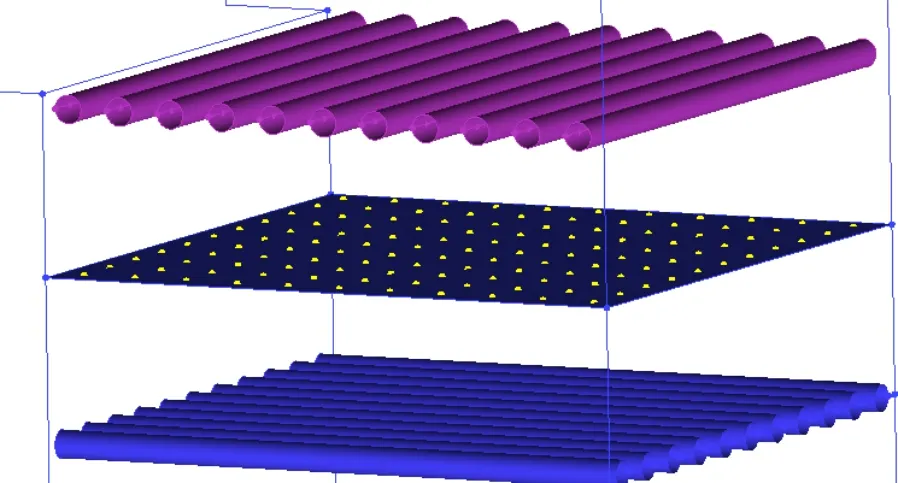
图6 采样点位置分布

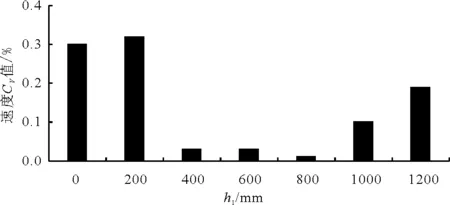
图7 h1对速度分布均匀性的影响

从图7可以看出，随着h1的增加，速度CV值整体呈先下降后上升的趋势。当h1=400、600、800 mm时，CV值在0.05%以下，速度分布较为均匀。在图8中可明显看出，h1过大或过小都会降低速度分布的均匀性。结合速度分布云图可知，由于h1的不同，栅条附近形成了不同的影响絮凝碰撞过程的涡旋结构。絮体沿着水流的主流方向运动，而这正是絮体混合强度和水力条件相互作用的主要来源[17]，因此良好的水力负荷分布条件是充分絮凝的前提条件。

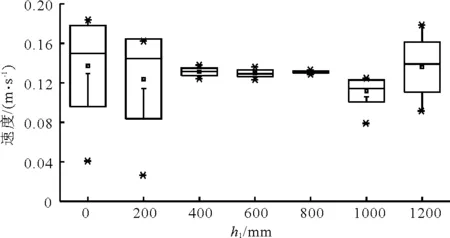
图8 栅条下截面速度分布箱线图

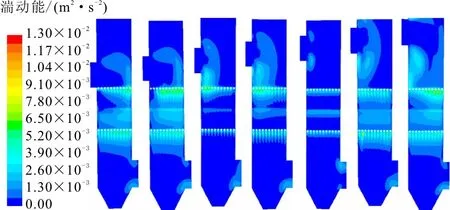
图9 x=0.45 m截面湍动能分布云图

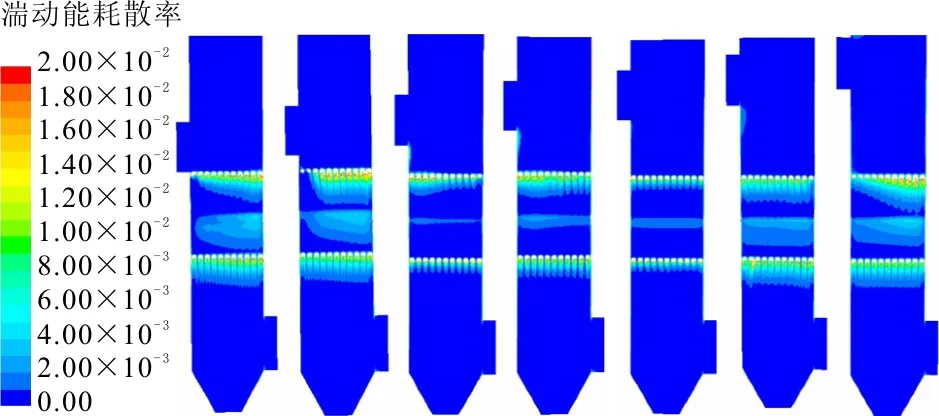
图10 x=0.45 m截面湍动能耗散率分布云图

絮凝过程和流场中的湍动能k和湍动能耗散率ε密切相关[2，18]。据图9和10可看出，湍动能k和湍动能耗散率ε的变化趋势基本相似，符合絮凝池内的掺混规律。从湍动能分布云图中可以看出当栅间距一定时，水流通过栅条改变了初始方向，导致了栅条后续区域的流场发生剧烈的变化，在这个过程中形成较长的尾迹线，并且相互影响。随着h1的增加，k值和ε值在栅条附近密集分布的部位也发生了明显变化，h1在400～800 mm范围内变化时，湍动能和湍动能耗散率分布较为均匀，利于絮体颗粒的充分絮凝。

4.2 宽深比对流场分布的影响

由于现行设计规范《室外排水设计规范》GB 50014-2006(2014年版)未对网格絮凝池的宽深比进行规定说明，研究以探求最佳宽深比为目标进行数值模拟。将进口顶部与出口底部之间的垂直距离作为池深，固定为4 150 mm，通过改变絮凝池的宽度(800、900、1 000、1 100、1 200、1 300、1 400、1 500、1 800、2 000 mm)，读取采样点速度数据，得到流场速度分布图11及速度相对标准偏差随池宽的变化图12，探求网格絮凝池的最佳宽深比。

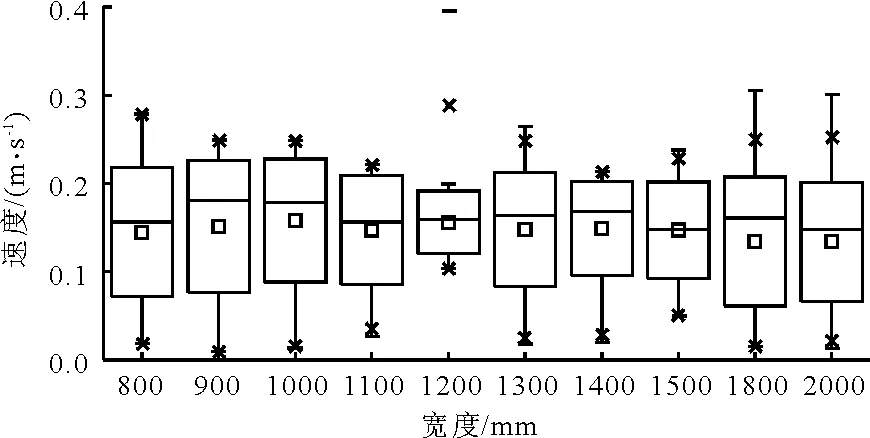
图11 不同池宽条件下截面速度分布箱线图

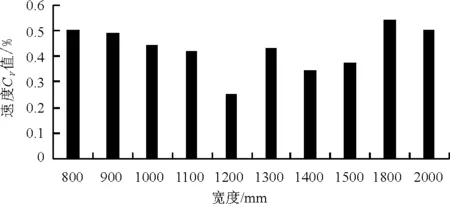
图12 不同池宽的絮凝池栅条下截面速度CV值分布

由图11和12可知，池宽在1 200 mm时，即宽深比为0.29左右时，由xy平面上各监测点得出的速度值相对最为集中，速度波动较小，此时CV值为0.25%。

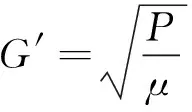
(3)

式中：ρ为水的密度，kg/m3;μ为动力黏度，Pa·s。

由公式(3)可知，涡旋速度梯度G′值与湍动能耗散率ε成正比关系。通过模拟结果中湍动能耗散率ε值，计算出涡旋速度梯度G′值，绘制池宽不同时G′的变化趋势，见图13。

由图13可知，池宽在800～1 000 mm内，竖井内的平均G′值呈递减趋势；在1 000～1 400 mm范围内，G′值又呈上升趋势，但变化不大，整体在26 s-1左右波动；池宽增加到1 500 mm及以后，水流受壁面“反弹”产生的惯性力远小于池宽为800～1 400 mm条件下的惯性力，使得黏性力作用加强，不同尺度的涡旋在更广的空间流域内发生衰减的概率和强度增加，涡旋速度梯度G′值迅速下降，从而不利于絮体的增长。

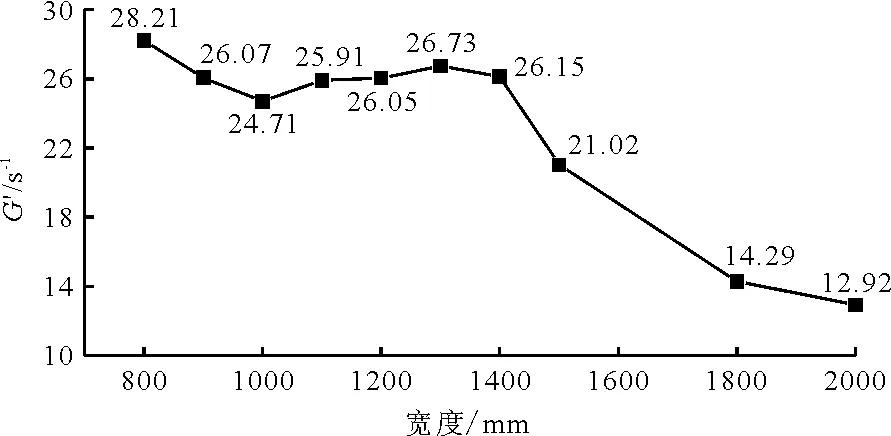
图13 不同池宽的絮凝池涡旋速度梯度分布

综合水力负荷均匀性和涡旋速度梯度G′值的双重影响，竖井内既要保证速度分布的均匀性，使得颗粒在运输、碰撞、絮凝过程中的流场局部差异性较小，又要确保有足够大的速度梯度G′值以实现颗粒的有效碰撞，以便形成密实的絮体；考虑到实际情况，800～1 000 mm的竖井宽度过小，不便于现场的施工安装，故建议网格絮凝池单个竖井的池宽在1 100～1 400 mm范围以内，宽深比在0.29左右。

5 结 论

研究采用标准k-ε湍流模型对网格絮凝池竖井进行了三维数值模拟，并验证了网格无关性，发现栅条边界层网格为6层，网格节点数在125×104左右时，模型对数值计算结果的干扰较小；经试验再次验证，数值模型可靠。模拟以速度分布、湍动能k值和速度梯度G′值等为评价指标，探求进口到首层栅条距离(h1)及宽深比对流场分布的影响，得出以下主要结论：

(1)随着进口到首层栅条距离(h1)的增加，流场死水区范围逐渐缩小，水力负荷均匀性在400～800 mm达到最优，此时速度CV值在0.05%以下，能够为絮体颗粒进行聚集和碰撞提供良好的水力条件。

(2)网格絮凝池单个竖井的宽深比在0.29左右时，良好的水力条件适合絮体颗粒的聚集和碰撞。结合实际情况，在4 150 mm的池深情况下，建议取池宽在1 100～1 400 mm内变化，以1 200 mm为最优设计。