Ding-内射模的函子伴随性
2018-09-10罗肖强
罗肖强
(四川文理学院 数学学院, 四川 达州 635000)
0 引 言
Gorenstein同调代数自20世纪60年代以来就受到众多学者的关注,对一些经典的同调代数很多学者给出了对应的Gorenstein同调代数结果. 2014年,EMMANOUIL等[1]研究了具有有限Gorenstein投射维数的模类的性质,通过具有有限Gorenstein投射维数的模类以及Gorenstein投射模类形成的稳定范畴构造了2对伴随函子, 并给出了Gorenstein同调代数维数的有限判定条件. 为深入研究Gorenstein内射模, 2008年,MAO等[2]引入了Gorenstein FP- 内射模, 得到了很好的性质. 2010年,GILLESPIE[3]将Gorenstein FP-内射模命名为Ding-内射模. 本文主要从稳定范畴的角度建立Ding-内射模的维数的有限判定条件.
1 预备知识
本节主要回顾Ding-内射模的定义,并给出具有有限Ding-内射维数的模类的基本性质.
定义2[2]设R为任意环, 如果存在一个HomR(FI,-)正合的内射R-模的正合列:
…→E1→E0→E0→E1→…,
使得M=ker(E0→E1),则称R-模M是Ding-内射的.
记DidR(M)和idR(M)分别为模M的Ding-内射维数和内射维数,利用标准方法可以定义模的Ding-内射维数.
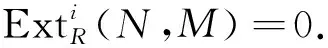
命题1[5]R-模M是Ding-内射的当且仅当存在一个R-模短正合列0→Q′→E→Q→0,使得E是内射模、Q′是Ding-内射模.
命题2设M为任意R-模,n为非负整数, 则下列条件等价:
(1) DidR(M)≤n;
(2) 存在R-模的短正合列0→M→Q→L→0, 使得Q是Ding-内射的并且idR(L)≤n-1;
(3) 存在R-模的短正合列0→Q′→B→M→0, 使得Q′是Ding-内射的并且idR(B)≤n.
证明由文献[6]可得 (1)⟺(2).
(2)⟹(3) 假设存在(2)中的短正合列, 因Q是Ding-内射的, 则由命题1可得短正合列
0→Q′→E→Q→0,
使得E是内射模、Q′是Ding-内射模.考虑下列拉回交换图:

由于idR(L)≤n-1, 于是idR(B)≤n. 因此存在R-模的短正合列0→Q′→B→M→0, 使得Q′是Ding-内射的并且idR(B)≤n.
(3)⟹(2) 假设存在(3)中的短正合列, 因为idR(B)≤n, 则存在短正合列
0→B→E→L→0,
使得E是内射模且idR(L)≤n-1.考虑下列推出交换图:
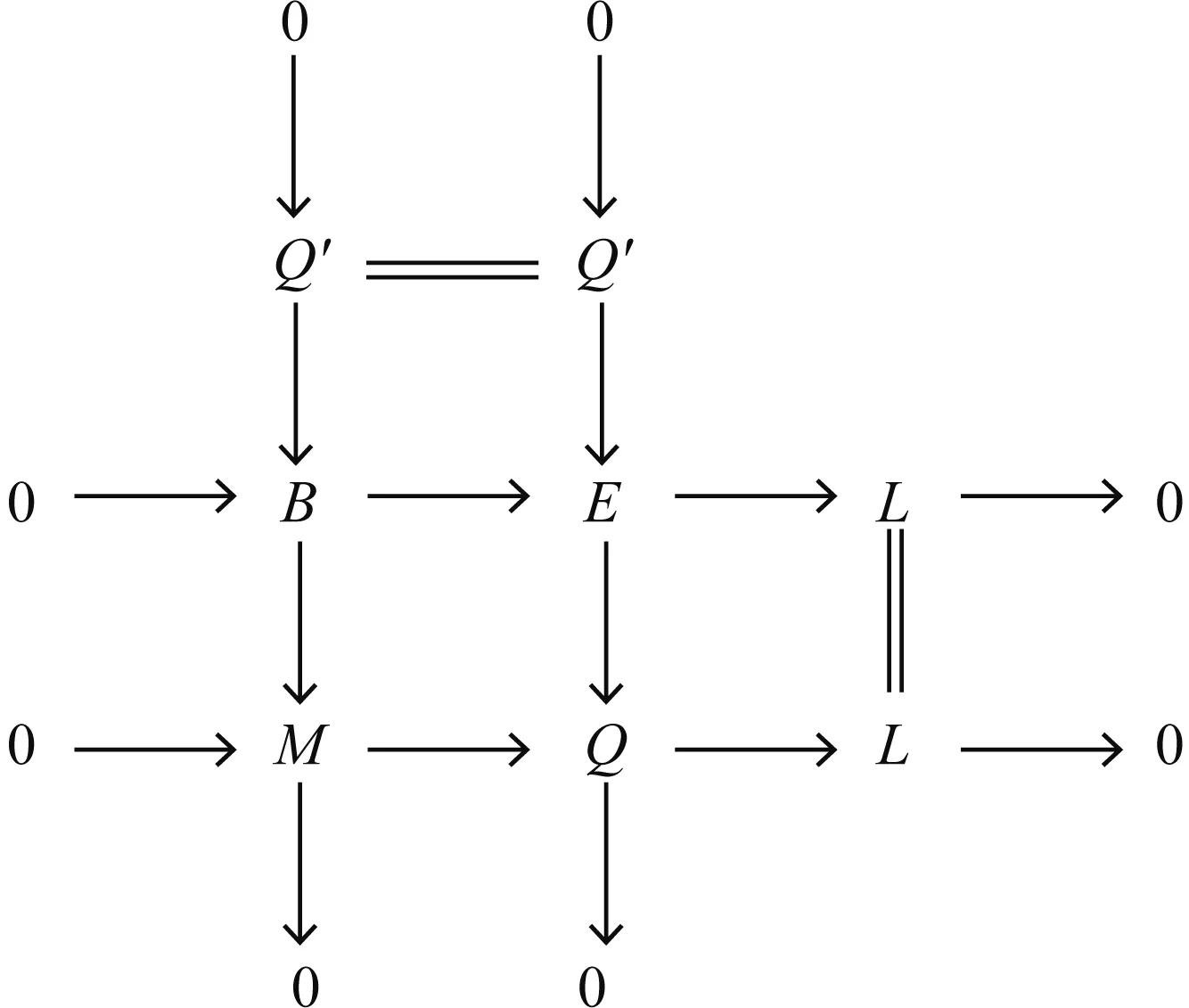
由文献[5]定理2.8可得,Q是Ding-内射的, 因此存在R-模的短正合列0→M→Q→L→0,使得Q是Ding-内射的并且idR(B)≤n-1.
推论1设R-模M有有限Ding-内射维数. 则

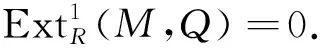

0→M→Q→L→0,

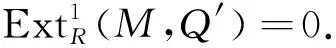
0→Q′→B→M→0,

引理2设M是任意的有有限Ding-内射维数的R-模.
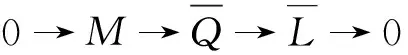
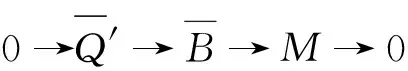
证明(i)假设存在(i)中的2个短正合列,考虑下列推出交换图:


(ii) 由(i)对偶可证:

2 关于有有限内射维数的模类的稳定性
设M,N是2个R-模.则所有可以通过具有有限内射维数的模分解的M到N的态射组成的集合是阿贝尔群HomR(M,N)的子群.记对应的商群为FI-HomR(M,N),并且对任意的f∈HomR(M,N),设[f]=[f]FI.接下来考虑所有的R-Mod,态射集为FI-HomR(M,N)的范畴FI-R-Mod.
引理3设M,N为2个有有限Ding-内射维数的R-模,f:M→N为任意态射.考虑下列2个R-模的短正合列:
和
其中,L,L′有有限内射维数,Q,Q′是Ding-内射的,则
(i) 存在态射g:Q→Q′,使得gα=α′f;
(ii) 如果g,g′:Q→Q′是2个态射,使得gα=α′f,g′α=α′f,则[g]=[g′]∈FI-HomR(Q,Q′);
(iii) 如果[f]=[0]∈FI-HomR(M,N),对任意的态射g:Q→Q′使得gα=α′f,则[g]=[0]∈FI-HomR(Q,Q′).

(ii) 设g,g′:Q→Q′是2个态射,使得gα=α′f,g′α=α′f:
则
(g-g′)α=gα-g′α=α′f-α′f=0,

因此存在态射h:L→Q′,使得g-g′=hβ.因为L有有限内射维数,所以[g]=[g′]∈FI-HomR(Q,Q′).
(iii) 设f由通过有有限内射维数的R-模I分解,即
则对I有下列短正合列:
使得E是内射的、I′有有限内射维数.由(i)知,存在γ′:Q→E和δ′:E→Q′,使得下列图可交换.

即有α′δ=δ′i且iγ=γ′α.因此(δ′γ′)α=(δ′i)γ=α′(δγ)=α′f.于是,对任意的态射g:Q→Q′使得gα=α′f,由(ii)可得,[g]=[δ′γ′]=[0]∈FI-HomR(Q,Q′).
设范畴FI-DI(R)和FI-FDI(R)是FI-R-Mod的全子范畴,他们的对象分别为Ding-内射模以及有有限Ding-内射维数的模.于是,FI-DI(R)是FI-FDI(R)的全子范畴.由引理2(i)和引理3可得,存在一个良定的加法函子:
μ: FI-FDI(R)→FI-DI(R),
且有
定理1加法函子μ: FI-FDI(R)→FI-DI(R)是嵌入函子FI-DI(R)FI-FDI(R)的左伴随.
证明设M有有限Ding-内射维数,T为Ding-内射模.则有短正合列:
使得Q是Ding-内射的并且idR(L)<∞.由伴随同构的定义,只需证明
[α]*: FI-HomR(Q,T)→FI-HomR(M,T)
是双射的并且在M,T处具有自然性.由引理3易得[α]*在M,T处具有自然性.
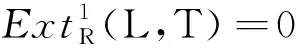
[α]*: HomR(Q,T)→HomR(M,T)
是满的,因此[α]*是满的.其次,设g:Q→T是任意的一个态射,使得
[gα]=[g][α]=[α]*[g]=[0]∈FI-HomR(M,T).
考虑下列交换图:

由引理3(iii),有[g]=0∈FI-HomR(Q,T).
推论2设M有有限Ding-内射维数,则下列条件等价:
(i)M有有限的内射维数;
(ii) 对任意Ding-内射模T有
FI-HomR(M,T)=0;
(iii) 存在一个短正合列
其中,Q是Ding-内射的并且idR(L)<∞,使得
[α]=[0]∈FI-HomR(M,Q).
证明(i)⟹(ii)和(ii)⟹(iii)显然.
(iii)⟹(i) 由定理1可知
[α]*: FI-HomR(Q,Q)→FI-HomR(M,Q)
是双射的.因此,如果
[α]*[1Q]=[1Q][α]=[α]=[0]∈FI-HomR(M,Q),
则
[1Q]=[0]∈FI-HomR(Q,Q),
由此可得Q是某个有有限内射维数的模的直和项,即Q有有限内射维数.再由Q是Ding-内射的,可得Q是内射的,于是M有有限内射维数.
证毕!
3 关于Ding-内射模类的稳定性
设M,N是2个R-模,则所有可以通过Ding-内射模分解的M到N的态射形成的集合是阿贝尔群HomR(M,N)的子群.记对应的商群为DI-HomR(M,N),并且对任意的f∈HomR(M,N),设[f]=[f]DI.接下来考虑的对象为所有的R-Mod,态射集为DI-HomR(M,N)的范畴DI-R-Mod,
引理4设M,N为2个有有限Ding-内射维数的R-模,f:M→N为任意态射.考虑下列2个R-模的短正合列:
和
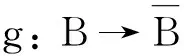

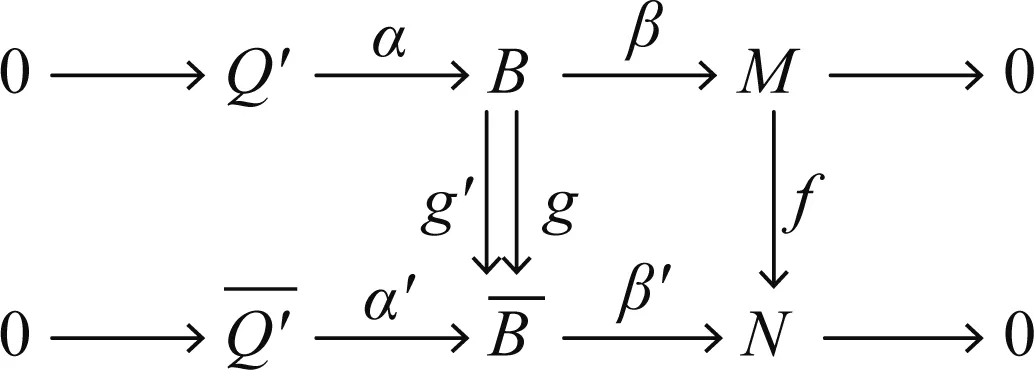

(iii) 设f通过Ding-内射R-模E分解,即
则对E,有下列短正合列


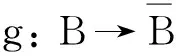
设范畴DI-FI(R)和DI-FDI(R)是FI-R-Mod的全子范畴,他们的对象分别为有有限内射维数的模以及有有限Ding-内射维数的模.于是,DI-FI(R)是DI-FDI(R)的全子范畴.由引理2(ii)和引理4可得,存在一个良定的加法函子
ν: DI-FDI(R)→DI-FI(R),
且有
定理2加法函子ν: DI-FDI(R)→DI-FI(R)是嵌入函子DI-FI(R)DI-FDI(R)的右伴随.
证明设M有有限Ding-内射维数,A有有限内射维数.则有短正合列
使得Q′是Ding-内射的并且idR(B)<∞.根据伴随同构定义,只需证明
[β]*: DI-HomR(A,B)→DI-HomR(A,M)
是双射的并且在M,A处具有自然性.由引理4易得[β]*在M,A处具有自然性.

[β]*: HomR(A,B)→HomR(A,M)
是满的,因此[β]*是满的.其次,设g:A→B为一任意态射,使得
[βg]=[β][g]=[β]*[g]=[0]∈DI-HomR(A,M).
考虑下列交换图:

由引理4(iii),[g]=0∈DI-HomR(A,B).
证毕!
推论3设M有有限Ding-内射维数,则下列条件等价:
(i)M是Ding-内射的;
(ii) 对任意有有限内射维数的模T都有DI-HomR(T,M)=0;
(iii) 存在一个短正合列
其中Q′是Ding-内射的并且idR(B)<∞,使得
[β]=[0]∈DI-HomR(B,M).
证明(i)⟹(ii)和(ii)⟹(iii)显然.
(iii)⟹(i) 由定理2,特别地
[β]*: DI-HomR(B,B)→DI-HomR(B,M)
是双射的.因此,如果
[β]*[1B]=[β][1B]=[β]=0∈DI-HomR(B,M),
则
[1B]=[0]∈DI-HomR(B,B),
因此可得B是某个Ding-内射模的直和项,即B是Ding-内射的,于是M是Ding-内射的.
