林木资产评估中市场法的应用研究
2018-09-10山西工商学院金融学院山西太原030000
(山西工商学院金融学院山西太原030000)
一、引言
随着林权制度改革的深入,林业生产要素的流动性不断增强,森林资源资产的有偿转让、抵押贷款、租赁等经济行为日益频繁,从而使林木资产评估的需求增多,为保障森林资源转让各方当事人的合法权益,规范开展森林资源资产评估工作,进行合理的价值评估就显得极为重要。然而我国在森林资源资产评估方面,对于评估方法中有关的技术经济参数的确定缺乏深入研究,大多停留在经验判断的层面上,导致评估结果与实际成交价格有很大的差异,并且对林业交易市场的发展产生了阻碍。本文通过对市场法进行改进,利用灰色关联度分析法确定各修正价格的权重,提出了用层次分析法来确定各因素的加权关联度,提升了利用市场法评估林木资产价格的准确性。
二、改进的林木资产评估方法
(一)市场成交价比较法。市场法是资产评估中最直接、最能反映林木资产市场价值的评估方法,包括市场成交价比较法、市场价倒算法等。本文重点研究市场成交价比较法的改进。市场成交价比较法是以相同或类似的林木资产的现行市场成交价格作为比较基础,估算拟评估的林木资产评估值的方法。市场成交价比较法要求对一个评估对象要选取三个以上参照交易案例,先把参考案例价格进行修正,并从评估资料、评估参数指标等的代表性、适宜性、准确性方面,客观分析参照交易案例,采用简单算术平均法、加权算术平均法、众数法等方法确定评估结果。以往在采用加权算术平均法时,权重一般是根据以往的经验确定,使得评估结果可信度不高。而本文采用灰色关联度分析法确定权重,在利用灰色关联分析确定关联度时,引入层次分析法来确定各因素的加权关联度,从而提高了评估值的准确度。评估值E的计算公式如下式中:n为参照案例的个数;Qi为第i个参照案例所占权重;Ei为第i个参照案例调整后的评估值。
(二)灰色关联分析。在市场法中,通过灰色关联度分析求出被评估资产的影响因素序列与其参照案例调整因素序列的相似程度。关联度数值越大,则被评估资产与其参照物的关联程度越大。利用灰色关联度分析法测定权数,不要求知道变量的分布,也不要求变量之间相互独立,计算量小,而且不致出现灰色关联度的量化结果与定性分析不一致的情况,所以比较适合对经济现象的分析。灰色理论对于数据样本的要求低,对于样本量的多少和样本有无规律同样适用,在分析和处理林木资产估价的相关数据上有其独特的优势,结果可靠度高,因此本文使用市场法评估林木资产时运用灰色关联分析求取权重。
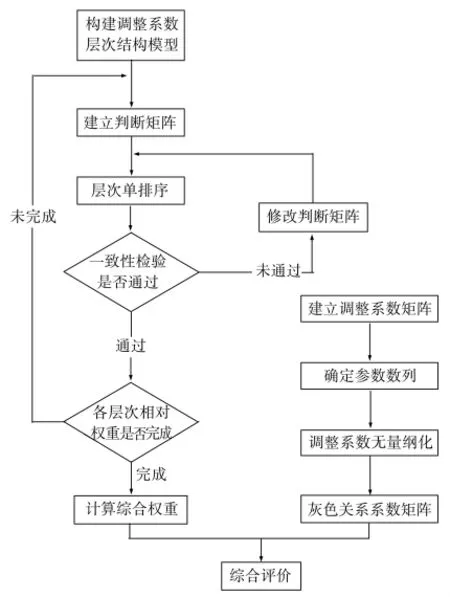
图1 综合AHP与GRA的计算
(三)层次分析法。层次分析法的计算思路是:首先对问题所涉及的因素进行分类,建立标度表;然后构造层次模型,从上到下依次为三层,即目标层、指标层、方案层;接着对每一层次各元素的相对重要性判断,构建判断矩阵;矩阵元素的值反映了人们对各因素相对重要性(或优劣、偏好、强度等)的认识;再进行层次总排序和层次单排序,在排序过程中,为避免产生片面性,应该对每个构建的判断矩阵进行一致性检验;最后计算出各层的方案相对于目标层的相对重要性权重,进而优选出方案。
(四)基于AHP-GRA的市场成交价比较法。运用灰色关联分析求权重时,关联度r是使用平权法求解的。因为关联度系数很多,信息分散,它的每一个值表明某一个指标两个数列的关联程度,为表现总体上两个数列的关联程度,对所有关联系数取平均值,即默认各因素的权重是相同的,但实际情况中,各因素的权值并不是关联系数的平均值。所以本文在利用灰色关联分析确定各调整系数的权重时,引入层次分析法来确定各因素的加权关联度。
综合层次分析和灰色关联分析的具体步骤如下:先以灰色关联分析确定指标初始矩阵并对指标进行无量纲化,计算灰色关联系数矩阵M。再利用层次分析法构建判断矩阵并进行层次单排序,对建立的判断矩阵进行一致性检验,若通过,则计算权重W;若不通过,再建立判断矩阵。最后进行综合评价,即关联系数矩阵M与权重W矩阵乘积,得到加权关联度,再利用加权关联度求出最终运用市场法评估林木资产价值的权重Q。见上页图1。
三、林木资产价值评估案例应用
某村拟转让一块面积为10hm2的落叶松成熟林,需要对其林木资产进行评估。根据资产清查结果,该小班蓄积量为161.1m3/hm2,林分株数为 765 株/hm2,平均树高 14.0m,平均胸径18.1cm,立地质量系数为0.88。按照资产性质和评估要求,从已收集以往的交易资料中选取5个交易案例参考,见表1。参照案例修正系数及交易价格统计结果见表2。

表1 评估案例和参照案例评价因子
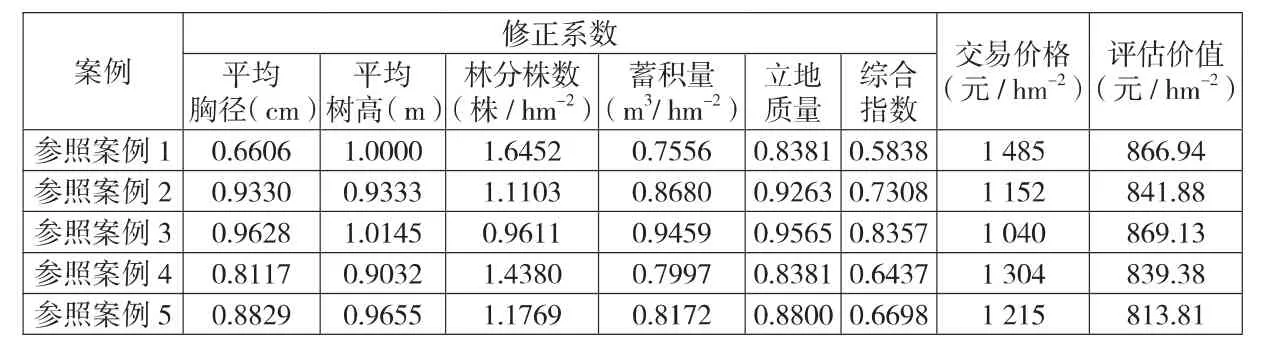
表2 参照案例修正系数与交易价格
(一)将数据进行初始化处理。设比较序列为:X0(k)={X0(1),X0(2),…,X0(5)}。参考序列为:Xi(k)={Xi(1),Xi(2),…,Xi(5)},i=1,2,…5。将数据进行初始化处理X0j,i=1,2,…5。得到表3。
(二)求取序列差。其中∣X0(k)-Xi(k)∣是每个参考数列X0曲线上的各点同比较数列Xi曲线上的各点差值。是两级的最小差,记为是两级的最大差,记为△max。

表3 初始化处理结果表

表4 序列差
(三)求参考序列与比较序列的灰色关联系数γ(Xi)。其中 γ(Xi)=(△min+ξ△max)/[ △0i(k)+ξ△max],ξ是分辨系数,0<ξ<1,取值 ξ=0.5。

表5 关联系数表
(四)建立层次分析模型。具体见图2。
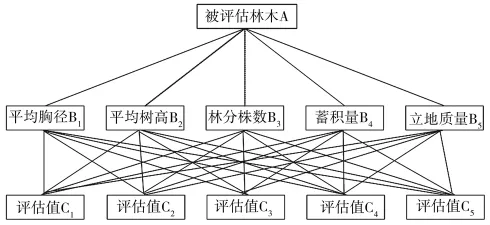
图2 层次分析模型
根据各调整系数对落叶松资产评估的影响,建立判断矩阵,具体见下页表6。
(五)层次单排序以及一致性检验。
1.计算判断矩阵B每一行的连乘积,Mi=得 M=[0.0833 6 9 4 0.0556]T。
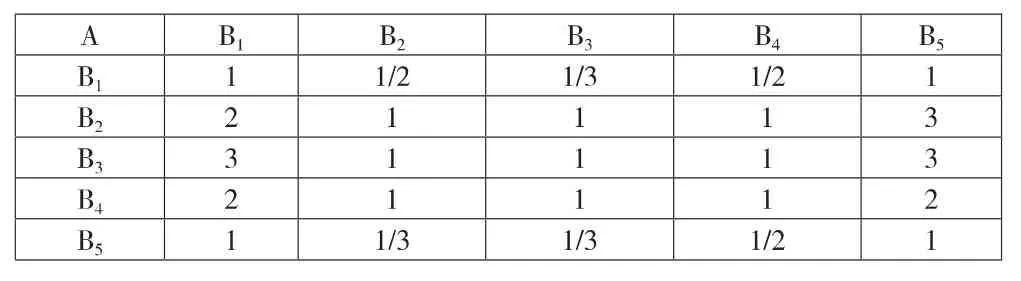
表6 判断矩阵

5.进行一致性检验,若 CR<0.1,则认为判断矩阵的一致性是可以接受的,否则需要对判断矩阵的元素进行修正,直到获得满意的一致性为止。

通过查表7,n=5,可得 RI=1.12,所以随机一致性比率:CR=CI/RI=0.0082/1.12=0.0073。

表7 平均随机一致性指标
通过以上计算我们可以得到 CR=0.0073<0.1,认为构建的判断矩阵具有满意的一致性。因此得出五个影响因素的权重为:0.1112,0.2615,0.2836,0.2411,0.1025。各个因素重要性的比较结果为(从大到小排列):B3>B2>B4>B1>B5,即林分株树>平均树高>蓄积量>平均胸径>立地质量。
(六)计算加权关联度。由灰色关联分析得到落叶松各调整因素的关联系数,用Mij表示:

利用层次分析法得到的落叶松各调整因素的权重用Wij表示:Wij=[0.1112 0.2615 0.2836 0.2411 0.1025]T。
那么加权关联度ri=Mij×Wij,得到各方案的关联度(见表8)。
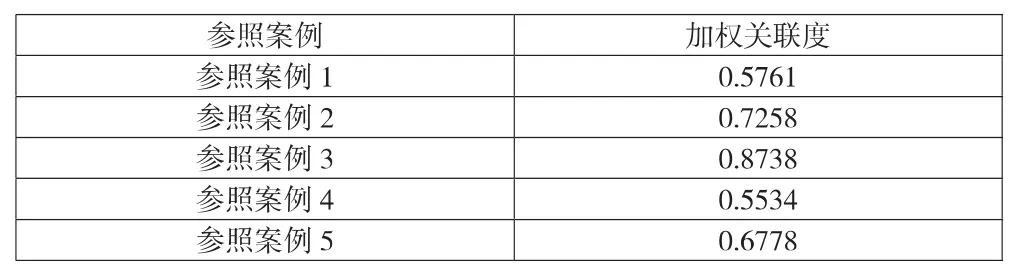
表8 加权关联度表

表9 权重表

而应用简单平均法求落叶松的评估值,结果为:

从上式可以得出,选择运用简单平均值还是综合AHP与GRA会对落叶松的评估值产生差异,基于AHP-GRA的市场成交价比较法的评估结果更科学、合理。
四、结论
本文从市场比较法出发,提出基于AHP-GRA的市场成交价比较法评估林木资产。这种方法比用简单平均值确定评估对象的资产价值更为合理,更具有说服力,为市场法评估林木资源价值提供了一种新的思路,为丰富和完善林木资产评估提供了一条新的技术途径,在评估实践上有推广应用价值。
当然,在运用该方法时应该注意,林木价格估算涉及的因素很多,不同树种需要考虑的林分影响因子不同。本文在落叶松林木价值评估时选取的参照因子,并不一定同样适用于其他树种,在今后的研究工作中,我们应该更为广泛地咨询专家意见,并结合实际情况确定相关影响因素。
