大展弦比无人机翼梁结构刚度优化设计

郭文杰 聂小华 王立凯 罗利龙 段世慧

摘要：以某型无人机翼梁结构为研究对象，应用结构拓扑优化设计技术对其进行刚度优化设计。将翼梁腹板划分为多种不同的拓扑优化设计子区域，以结构刚度最大化为设计目标，考虑子区域材料用量、结构强度、翼尖变形等约束，对比了不同子区域划分方式下的设计结果，获得了适用于大展弦比机翼翼梁结构拓扑优化的腹板子区域划分方式，对原始翼梁结构进行改进，改进后的翼梁结构满足强度、刚度设计要求。

关键词：大展弦比;翼梁;拓扑优化，减重;强度

中图分类号：V214.19 文献标识码：A

经过几十年的发展，结构拓扑优化设计技术已经成为结构概念设计阶段的重要技术手段[1]。随着飞行器性能的不断提升，飞行器结构的设计要求也变得非常苛刻。尽管结构拓扑优化设计技术已经被证实为一种高效的结构概念设计方法，但是在结构设计领域，尤其在航空航天结构轻量化、高性能设计过程中面临着巨大挑战[2]。

无人机（UAV）的出现大大提高了作战、侦察等的效率，结构重量（质量）无疑是制约无人机性能的重要因素之一[3]。大展弦比、长直翼高空巡航无人机的应用前景十分广阔[4]。翼梁作为该类无人机中重要的承载部件之一，承受着弯、扭等复杂载荷。如何以最轻的结构重量承载众多重要的载荷是设计人员不变的追求[1]。应用结构拓扑优化设计技术对大展弦比机翼翼梁结构进行设计，如果将整个腹板作为单一拓扑设计区域，由于翼尖处结构应力水平低，一般很难获得清晰的结构构型，这就难以对工程问题提供有效的指导，结构往往存在重量冗余。Zhao等提出了基于子结构的结构拓扑优化设计技术，对翼面结构进行拓扑优化子区域划分，在原理上证明了该方法在获得翼面加筋清晰布局上的可行性[5]。

本文以结构拓扑优化设计技术为基础，在Zhao等[5]工作的基础上，考虑结构强度、翼尖变形等约束，对某大展弦比无人机翼梁结构开展刚度优化设计。将翼梁腹板划分为多种不同形式的拓扑设计区域进行优化，分别约束不同拓扑设计区域的材料用量，得到了清晰的结构构型，应用该方法对原始翼梁结构进行重构设计，优化后的结构满足强度、刚度设计要求，减重达6%。

1 翼梁原结构设计方案分析

单梁直机翼无人机在服役过程中，气动、弯、扭等载荷通过蒙皮、长桁最终汇集到翼梁，通过翼梁将载荷传至机身。这类飞行器主梁与机身的连接相对简单，翼梁与机身框通过各种接头连接。典型长直机翼无人机如图1所示[6]。

本文以某无人机单侧翼梁为研究对象，对其设计进行改进。图2给出了翼梁的原始结构示意图。其中，翼梁长4m，高0.17m，上下缘条厚度均为12mm，翼根处缘条宽度为80mm，翼尖处宽50mm，缘条由根部至翼尖均匀过渡。梁腹板厚6mm，腹板上两个设计孔在图中标出，其余孔为减重孔。此外，腹板局部减薄，减薄区域腹板厚度为3mm。翼梁根部通过连接件与机身框相连，连接件与翼梁根部连接区域沿展向长100mm。翼梁材料弹性模量为2.1×10¹¹Pa，密度为7.9×10³kg/m³，泊松比为0.3。

首先对原始翼梁结构进行有限元离散，本文不考虑连接件构型对设计结果的影响，连接处以固定边界条件描述，整个翼梁均以六面体网格离散，约束连接部位相应节点所有自由度。翼梁总重67.65kg，取某一工况为例，翼梁受载后应力及位移云图分布如图3，图4所示。

可以看出，原始设计方案最大变形发生在翼尖处，值为31.76mm，最大米泽斯（Uon Mises）应力出现在翼根处，值为230.1MPa。去除应力集中区，大部分区域应力水平较为均匀，靠近翼尖处结构应力水平很低，而该区域却留有大量的材料，尤其靠近翼尖处腹板材料冗余量较大。

为提高材料利用率，在保证结构性能的前提下最大限度地减轻结构重量，我们应用结构拓扑优化设计方法对翼梁腹板区域进行优化设计。

2 翼梁结构拓扑优化设计

实际上，结构拓扑优化设计技术是概念设计阶段较为常用的技术之一，其目的是为获得具有指导意义的结构材料分布。本节首先对结构拓扑优化设计理论进行简要叙述，随后建立基于拓扑设计子区域的翼梁结构拓扑优化设计的数学模型，将腹板分成多个独立的拓扑子区域，分别约束不同设计区域的材料用量、应力等，得到满足设计要求的结果。

2.1 拓扑优化设计理论

通常，结构拓扑优化设计是通过材料插值完成的。将单元力学参数与其材料属性建立关联，引入单元伪密度的概念，建立插值函数。图5给出了典型的結构拓扑优化设计示意图。

较具代表性的是Bendsoe等提出的实体各项同性材料惩罚（Solid Isotropic Material with Penalty，SIMP）模型[7]，其材料插值表达式为：式中：E_i（η_i）为拓扑设计单元i的单元材料弹性模量，η_i为其单元伪密度，ρ为惩罚因子，E⁰为单元充满材料时的弹性模量。通常p取值为3。

2.2 翼梁结构拓扑优化设计数学模型

一般的结构拓扑优化设计问题往往以刚度最大（或重量最小）为优化目标，同时设定一定的约束条件，如材料用量、位移、模态等[8～11]，通过优化算法寻求设计变量的合理分布，进而获得结构的构型分布。首先给出传统的刚度最大化问题的结构拓扑优化设计问题的数学模型：式中：η为拓扑设计单元伪密度变量;η_i为单元i的伪密度设计变量;n为拓扑设计单元数目;C为总体应变能函数，u为全局位移矢量，K为总体刚度矩阵，F为系统所有节点载荷，V和V_u分别为拓扑设计区域材料用量分数及其上限。s_j及s_ju分别为第j个设计约束及其上限，这种约束可与是应力、位移、模态等。

对于将腹板划分为多个拓扑设计区域的翼梁优化问题，其材料用量分数约束一项可以写成：

V_k≤V_ku（3）式中：V_k及V_ku表示编号为k的拓扑设计区域的材料用量分数及其上限。

同时，引入不同设计区域的应力及翼尖变形约束：式中：str_k和str_ku分别为编号为k的设计区域的最大应力及其上限;dis_t和dis_tu表示翼梁上缘条翼尖处变形最大值及其上限。

图6给出了典型的翼梁结构腹板分区拓扑优化示意，其中N表示拓扑优化子区域的数量。实际上，传统的翼梁优化设计可认为是N=1的情况。

2.3 翼梁结构拓扑优化设计

本节针对该无人机机翼翼梁进行拓扑优化设计，重新建立拓扑优化有限元模型，在原始结构的基础上，将腹板填实成等厚6mm，除两个设计孔保留以外，填实所有减重孔。仍然采用六面体网格离散，单元尺寸3mm，共计354952个单元。

约束翼梁每个拓扑设计区域的最大应力不大于245MPa，翼尖最大变形不超过32mm，分别采用不同的设计区域划分方式对翼梁进行拓扑优化设计。图7～图10给出了腹板的不同拓扑区域划分方式，其中图7、图8划分多个拓扑区域但只约束其材料总用量分数上限为0.3，图9、图10腹板划分为多个拓扑设计区域，每种颜色代表一个单独的拓扑设计区域，对不同的拓扑设计区域分别约束其材料用量分数上限为0.3。

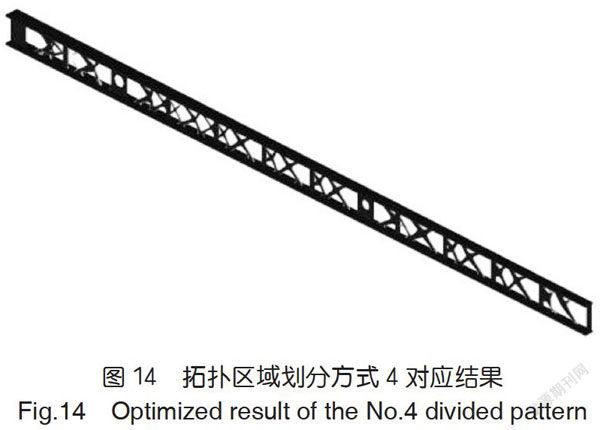
通过优化，我们得到了不同拓扑区域划分方式对应的结构构型。构型分别在图11～图14中给出，其中深色区域表示有材料部分。

对比优化结果可见，不同的腹板拓扑区域划分方式、材料用量约束方式会得到不同的结果，对比拓扑区域划分方式1和方式3可知，拓扑区域划分形式相同时，分别约束不同拓扑区域的材料用量分数时，其优化结果会在靠近翼尖附近处保留相对较多的材料;同样，如果将拓扑区域划分的较多，并分别约束不同的拓扑区域的材料用量分数，划分区域数量多的，其构型也较为清晰，如划分方式3与划分方式4的对比。

对比上述4种构型可见，将腹板划分为多个拓扑设计区域并分别约束不同设计区域的材料用量，可以在翼尖附件获得更清晰的材料分布，能够为概念设计阶段提供更多的指導。因此我们选取图14所得的结果对原方案进行改进，以求在保证结构性能的前提下，减轻结构重量。

3 优化结果重构分析

本节根据拓扑优化所得结果，对原始结构构型进行改进与分析。事实上，将腹板划分为多个拓扑设计区域并分别约束其材料用量上限，这样得到的设计结果必定会使每个区域均有适当的材料分布，但在对设计结果进行重构时，设计人员往往要结合工程经验对其进行取舍。

对于传统的设计方式，将梁的整个腹板作为一个设计区域并仅约束一个材料用量分数时，翼尖附近材料分布很少，这说明翼尖附近材料的承载作用相对于翼根附近较弱，使用不包含工程经验的优化算法进行优化时，会去除大量的承载作用较弱的材料。

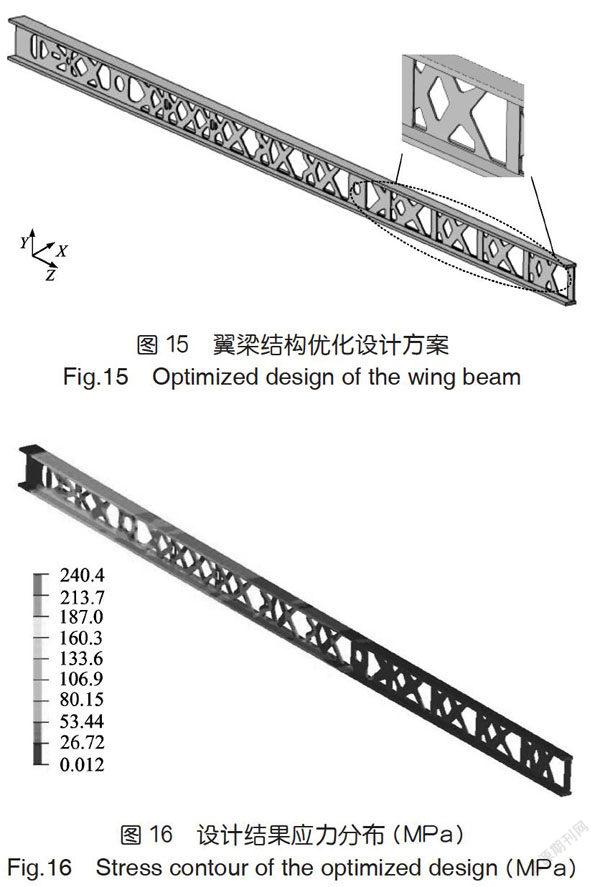
本工作结合原有设计，参照通过本文的设计方法，对原始结构进行重构，经过多轮迭代分析，得到了如图巧一图17所示的设计方案。其翼梁重量为63.63kg，较原始设计减少约6%。

对优化设计方案施加与原始结构相同的载荷与边界条件后，进行计算，得到翼梁结构的应力、变形分布图如图16、图17所示。

图巧所示的设计方案中，除参照拓扑优化设计结果以外，还将腹板厚度进行了一定的减薄处理，减薄区域的腹板由6mm变为4mm。优化前后翼梁结构应力、应变、重量等对比见表1。

对比优化前后的设计结果，优化后结构最大变形变为30.80mm，较原始设计减小0.96mm，最大应力在优化后变为240.1MPa，虽然较原始设计有所增大，但未超过约束上限245MPa，同时结构减重6%。

事实上，上述优化问题的本质是求解一个数学问题，当构建了合适的优化模型后，优化算法便开始搜寻问题的最优解，当使用结构拓扑优化技术按传统的方式设置设计区域时，优化问题本身并没有不妥，只是这样得到的设计结果很难为翼尖部位的材料分布提供指导，而引入了拓扑优化子区域，翼尖部位能够获得较为清晰的材料分布形式，能够快速为工程人员提供指导，而通过计算发现这样的方法在满足结构性能要求的同时又减轻了结构重量，因此认为其是可供工程技术人员参考的一种行之有效的优化设计方法。

4 结束语

本研究以结构拓扑优化设计为基础，对典型的大展弦比无人机机翼翼梁结构进行刚度优化设计。采用将翼梁腹板划分为不同的拓扑设计区域并分别约束不同区域的材料用量分数的方式，获得了清晰的翼梁腹板材料分布，结合工程经验，对原始设计方案进行改进，改进后的设计在满足设计要求的前提下，获得了减重6%的效果，具有一定的工程意义。

参考文献

[1]Zhu J H，Zhang W H，Xia L.Topology optimization in aircraftand aerospace structures design[J].Archives of ComputationalMethods in Engineering，2016，23（4）：595-622.

[2]Sigmund O，Maute K.Topology optimization approaches[J].Structural and Multidisciplinary Optimization，2013，48：1031-1055.

[3]沈惺，王和平.无人机设计参数对结构重量的影响分析[耳机械科学与技术，2013，32（9）：1272-1275.