基于灰色神经网络的港口货物吞吐量预测算法
2018-09-10胡克满蒋勇王顺林胡海燕
胡克满 蒋勇 王顺林 胡海燕


[摘要]通过对港口货物吞吐量影响因素的分析,运用了灰色模型理论选取部分已知信息计算未知信息,结合了人工神经网络系统对模型进行优化,给出了基于灰色神经网络的港口货物吞吐量预测算法,通过计算机仿真实验证明,并将港口货物吞吐量的实际值和预测值进行比较与误差分析,能够较好的进行港口货物吞吐量的预测,也适用于其他方面的预测分析,具有一定的实际应用价值。
[关键词]神经网络;灰色理论;港口货物吞吐量;预测
[中图分类号]TP183;U691.71 [文献标识码]A [文章编号]1005-152X(2018)02-0068-05
1 引言
随着国家战略“一带一路”步伐的不断推进,“21世纪海上丝绸之路”战略的实施,国际贸易活跃,经济的发展拉动了物流的需求。港口物流是国内外物流重要的组成部分,近几年港口物流发展迅速,从过去单一的货物交易场所转变为国内外物流链上的关键点之一。无论是发展海洋经济还是促进港口经济发展,国家对港口的建設和投入力度也在加大,对港口的作用也提出了更高的要求。为了迎接新的市场挑战,提升港口服务能力,港口之间的竞争也越来越激烈,国内港口在新的时代下也做出了新的调整,如:苏州港、常熟港、张家港三港合一;宁波港和舟山港也两港一体化组建宁波舟山港等。以宁波舟山港为例,2015年宁波舟山港货物吞吐量达8.9亿t,跃居全球第一,集装箱吞吐量达2 063万TEU。港口货物吞吐量关系到集疏运系统、港口通过能力的设计与规划,有效的对港口货物吞吐量进行预测,可以为港口的规划设计、集疏运系统建设、货物仓储等提供重要的技术指标。港口货物吞吐量大小的预测在确定港口的基础设施建设方面、泊位选址、港口经营模式、总体布局等方面均起到重要的影响作用。根据预测结果进行决策时,如果预测值过大,而实际货运吞吐量小,将造成不必要的基础设施建设资金的投入;如果预测值过小,而实际货运吞吐量大,会导致货物的积压,不能最大限度的发挥港口的作用,也同样是资源的浪费。由此可见,对港口货物吞吐量大小有效的预测在港口建设过程中有着积极的作用。
由于港口货物吞吐量预测的重要性,也因此在近几年也受到国内外专家学者们的关注,主要分为定性预测和定量预测两种。其中定性预测方法主要有主观概率法、情景预测法、货源调查法等;定量预测方法主要有回归分析法、时间序列预测法、灰色预测法、人工神经网络法等。定性预测法具有灵活性好、操作简单等特征,但是其过于依赖个体的经验判断,容易受到个体之间的差异和主观因素的影响,所以定性预测方法比较适合于港口货物吞吐量发展趋势的预测;定量预测法可以较好的预测港口货物吞吐量的大小值,但是往往对原始数据和预测指标的选择依赖较大,理论上原始数据越全面其预测结果也将越准确,计算量也随之增大。本文提出一种基于“部分信息”数据的预测方法,既可以通过预测值判断港口货物吞吐量的发展趋势,又可以较好的获得港口货物吞吐量的估计值。
在预测港口吞吐量的过程中,预测值受到诸多因素的影响,主要包括政治、经济、文化、社会、技术、环境等方面。在众多的因素中筛选影响因素是至关重要的,例如:国内生产总值(GDP)、三次产业(第一产业:农业(包括种植业、林业、牧业、副业、渔业),第二产业:工业(包括采掘业、制造业、自来水、电力、蒸汽、热水、煤气)和建筑业,第三产业:除第一、第二产业以外的其他各业)、进出口总额等,但是这些信息相对于港口货物吞吐量影响的因素仍然是属于“部分信息”。灰色系统理论可以根据“部分已知信息”进行分析,所以可以运用灰色理论对港口货物吞吐量进行预测。而人工神经网络的特征具有较强的自适应性与自学习能力,本文将灰色理论和人T神经网络相结合,从而优化港口货物吞吐量的预测模型,提高预测值的精确度。
2 灰色理论数学模型
灰色理论数学模型是由我国著名专家邓聚龙教授首次提出的,为灰色理论后续的发展奠定了基础。灰色理论数学模型的主要特征是可以利用部分已知信息解决部分未知信息的不确定性的系统问题。灰色关联度分析法是灰色理论系统的关键技术之一,通过时间和不同对象的变化而构建其关联性。具体步骤如下:
灰色理论数学模型对原始数据参数按照序列进行累加,使得累加后的数据具有一定的规律,然后再对数据进行曲线拟合。设时间数据序列为x0:
x0 =(x0t|t=1,2,…,n)=(x01,x02,…,x0n)
(1)
灰色模型对时间数据序列x0进行累加处理,并获得新的时间数据序列x1,其中设第t时刻的数据为x1t,x1t为原始时间数据序列x0的前t项的总和,即:根据新构建的数据序列x1,构建方程,得:整理方程(3),得到解为:
其中x1't是数据序列x1的估计值,另对x1't进行减法处理,得到x0的预测值为x0't:
灰色数学模型是将时间序列数据x0转换成微分方程,通过微分方程利用系统信息得到模型量化结果,因此可以在仅获得部分已知信息的情况下,估算部分未知信息从而获得预测值。
3 BP神经网络模型
人工神经网络模型在人工智能方面得到快速的发展和广泛的应用,人工神经网络就如同人脑的神经元网络对信号进行逐层处理,按照一定的数学规律构建输入层与输出层之间的复杂网络结构。输入层、隐含层和输出层之间,每一层的运算结果都会使得神经元保持不同的状态,也将影响下一层的神经元运算结果。为了能够满足运算结果,通常设定输出层的允许误差范围,根据误差比较结果反向传播并进行多次迭代运行直到误差满足条件,或者完成规定的迭代次数要求,图1为BP神经网络拓扑结构示意图。
图1中X1,X2,…,Xn为神经网络输入参数,计算结果输出值表示为y1,y2,…,Ym,wij和Wjk为神经网络模型的权值,神经网络的输人参数X1,X2,…,Xn和输出值Y1,Y2,…,Ym之间是白变量和因变量的关系,自变量和因变量之间构成了函数映射关系。
神经网络的输人参数是函数的自变量,其计算结果输出值为函数的因变量。由i个函数的白变量与i个函数的因变量构成函数映射关系。
4 灰色神经网络模型的构建
多个因素参数的灰色神经网络数学模型方程表示为:式(6)中系统模型的输出参数为y1系统模型的输人参数为y2,y3,…,yn,,a,b1,b2,…,bn-1,为系统网络模型的方程系数。时间序列相应的函数为:设:将式(7)和式(8)整理后得到:
将式(9)映射到BP神经网络中,并获得n个参数作为输入层数据,目标函数为输出1个预测估算值的灰色神经网络模型,灰色神经网络模型拓扑结构如图2所示。
其中,灰色神經网络模型中的输人参数为X1,X2,…,Xn,模型的权值表示为wij,输出层Y1为灰色神经网络系统模型的目标函数。
本文针对货运量(万t)、居民消费价格总指数、商品零售价格总指数和三产等作为模型的输人参数,并构成相关的数组,预测值为当年的港口货物吞吐量,定义为1维数组,基于灰色神经网络的港口货物吞吐量预测算法模型流程如图3所示。
5 实验结果与分析
灰色神经网络系统原始数据以宁波港口1985-2016年的港口货物吞吐量(万t)Y1、货运量(万t)X1、居民消费价格总指数X2、商品零售价格总指数X3、第一产业X、第二产业(建筑)X(1)5、第二产业(工业)X(2)5和第三产业X6等作为输入和输出数据进行测试与验证。详见表1,表1中港口货物吞吐量(万t)为输出量;影响因素包括:货运量(万t)、居民消费价格总指数、商品零售价格总指数、第一产业、第二产业(工业)和第三产业等为输入量,由于第二产业(建筑)对港口货物吞吐量的贡献相对较小,所以以第二产业(工业)数据代替第二产业的情况,这样可以相对减少误差率。表1中居民消费价格总指数与商品零售价格总指数均设定为1978=100。所有原始数据均来自宁波市统计局的《宁波统计年鉴》网络信息资料,详见参考文献。
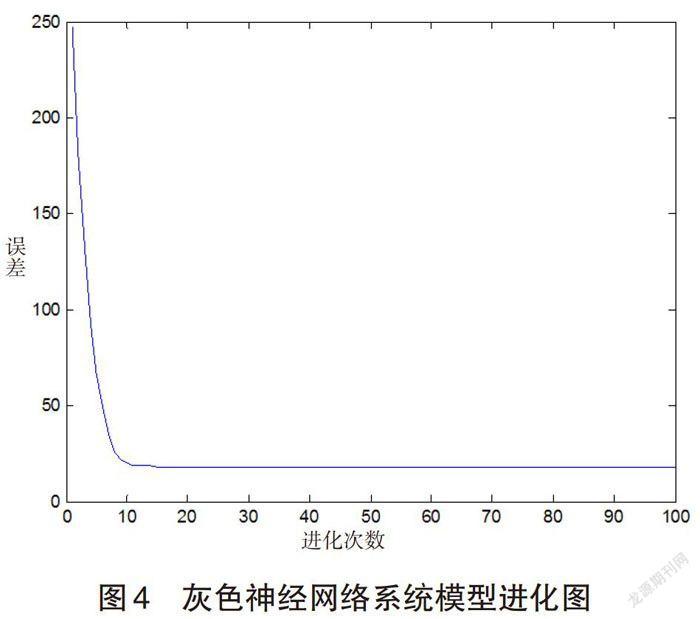
在进行测试时,需要对上述数据做简单的数据处理,由于数据量较多,选取了2000-2010年间的数据作为系统模型的训练集,通过多次迭代误差分析设定系统的收敛条件如图4所示,通过训练集数据的训练对2011-2014年的数据进行预测与比较,结果如图5所示。
由图4可见,灰色神经网络系统具有较好的收敛性,通过训练和进化获得参数对未知的港口货物吞吐量进行预测。图5为灰色神经网络系统对2010-2014年的港口货物吞吐量的预测结果。
由表2可知,通过灰色神经网络数学模型对过去数据的训练与学习,通过少量已知的数据顸测港口货物吞吐量,其中货运量(万t)、居民消费价格总指 数、商品零售价格总指数、第一产业、第二产业(T业)和第三产业等为输人参数,这些数据相对比较容易获得,具有一定的普适性。其中2011年灰色神经网络系统的预测值与实际值接近,其平均相对误差为1.36%,2010-2014这五年的平均相对误差仅为2.88%。由此可见,本文方法利用上述六种相对少量的信息有效的预测了港口货物吞吐量,具有一定的应用价值。
6 结论
港口货物吞吐量是现代港口物流中重要的指标之一,其结果也将直接影响港口的经营策略和港口发展动态规划调整等,而影响港口货物吞吐量的因素非常多,比如:政治、经济、交通设施、文化差异、自然环境、气候变化等,较多的影响因素使得人们无法较好的对当年的港口货物吞吐量进行预测。本文利用灰色理论的已知部分信息估算部分未知信息,结合人工神经网络的自学习能力和适应性的特征,选取了货运量(万t)、居民消费价格总指数、商品零售价格总指数、第一产业、第二产业(工业)和第三产业等为港口货物吞吐量的预测依据,通过灰色神经网络系统的优化,实验结果证明较好的预测了当年的港口货物吞吐量。由于本文的实验数据以宁波港数据为基础,获得数据有限,如果能够更加全面的收集数据作为训练样本,该模型的预测值可能将更优,该方法也可以适用于其他领域的预测分析,具有一定的应用和推广价值。