纤维沥青混凝土蠕变性能试验研究

陈丽芳 张森 黄春水

摘 要：通过不同纤维体积率和长径比的纤维沥青混凝土的弯曲蠕变试验，研究纤维体积率和长径比对混凝土蠕变变形、蠕变速率、蠕变柔量和卸载瞬时回弹模量的影响，建立了纤维沥青混凝土蠕变速率、蠕变柔量和卸载瞬时回弹模量的计算模型。试验研究和理论分析表明：纤维含量特征参数能综合反映纤维体积率和长径比对沥青混凝土蠕变速率、蠕变柔量和卸载瞬时回弹模量的影响。在本文试验范围内，纤维沥青混凝土最佳纤维体积率为0.35%，长径比为324，纤维含量特征参数为1.13。

关键词：纤维沥青混凝土；黏弹性能；蠕变试验；纤维含量特征参数

中图分类号：U416.217 文献标识码：A 文章编号：1003-5168（2018）08-0102-06

Experiment Research on the Creep Performance of Fiber

Reinforced Asphalt Concrete

CHEN Lifang1 ZHANG Sen2 HUANG Chunshui1

（1. College of Civil Engineering， Xuchang University，Xuchang Henan 461000；2. Henan Province Highway Engineering Bureau Group Co. ， Ltd.，Zhengzhou Henan 450052）

Abstract： Based on the flexural creep test of fiber asphalt concrete with different fiber volume fractions and aspect ratios， the influence of fiber volume fraction and aspect ratio on the creep deformation， creep rate， creep compliance and unloading momentary modulus of resilience of asphalt concrete was studied， calculation models for the creep rate， creep compliance and unloading momentary modulus of resilience were established. The experimental study and theoretical analysis show that， the fiber content characteristic parameter can reflect comprehensively the influence of the fiber volume ratio and fiber aspect ratio on the creep rate， creep compliance and unloading momentary modulus of resilience of asphalt concrete； within the scope of the test in this article， the optimum fiber volume ratio， fiber aspect ratio and fiber content characteristic parameter are 0.35%， 324 and 1.13 respectively.

Keywords： fiber reinforced asphalt concrete；viscoelastic performance；creep test； fiber content characteristic parameter

沥青混凝土是一种典型的黏弹性复合材料。目前，主要以单轴压缩蠕变、三轴压缩蠕变和小梁弯曲蠕变等试验为基础[1-3]，以阻尼器和弹簧等黏弹性基本元件组合出不同的黏弹性力学模型[4-7]，研究温度、加载应力水平等对沥青混凝土黏弹性能的影响[8-10]。由于纤维的加入能显著改善沥青混凝土的路用性能，因此對纤维沥青混凝土黏弹性能的研究得到了越来越多的重视[11]。例如，Benedito[12]通过动态和静态三轴试验研究了纤维掺量和长度对冷拌沥青混凝土力学性能的影响；郭乃胜[13，14]通过聚酯纤维沥青混凝土的压缩蠕变试验，运用Burgers模型和修正的Burgers模型，研究了一种纤维长度在不同掺量下对沥青混凝土蠕变加载阶段粘弹性能的影响，建立了考虑纤维掺量影响的纤维沥青混凝土粘弹性力学模型；封基良[15]通过拉拔试验，分析了纤维长度对沥青混凝土性能的影响。但是，现有的研究还存在许多亟待解决的问题，如纤维长径比和体积率对蠕变变形、蠕变速率、蠕变柔量等试验参数的影响等。为此，本文以AC-13F混合料为基体，以纤维体积率Vf和长径比Ra为参数，在马歇尔试验确定的最佳沥青用量下，进行小梁弯曲蠕变试验，研究纤维体积率和长径比对纤维沥青混凝土蠕变试验参数及黏弹性能的影响。

1 材料与试验

试验采用70号道路石油沥青和聚酯纤维。长径比Ra为162、486和649的纤维，其体积率Vf取0.35%；长径比为324的纤维，其体积率Vf分别取0.17%、0.35%、0.52%和0.69%。集料经过筛分、清洗、烘干后与石灰岩矿粉回配成AC-13F型级配中值[16]。通过标准马歇尔试验分别确定基体沥青混合料及不同纤维体积率和长径比的沥青混合料的最佳沥青用量OAC[17]。将设计的聚酯纤维沥青混合料轮碾成型为300mm×300mm×50mm的试件，然后切割成250mm×30mm×35mm的小梁试件，并在多功能材料试验机上进行15℃弯曲蠕变试验（见图1），用砝码进行加载。

蠕变荷载为同条件下小梁弯曲破坏荷载的10%。共进行了8组，每组重复3根小梁试件的蠕变试验。试验前，将试件置于环境箱中保温3h。试验过程中，用与数据采集系统相连的千分表采集蠕变试验过程中小梁的跨中挠度[dt]，每隔1s采集一次数据并绘制出跨中挠度-时间关系曲线；当小梁试件进入加速蠕变阶段时卸去荷载，继续采集卸载后30min内的小梁跨中挠度数据。按式（1）至式（5）计算蠕变弯拉应力[σ0]、弯拉应变[εt]、蠕變劲度模量[St]、蠕变柔量[Jt]和蠕变速率[εs]：

[σ0=3LP02bh2×10-6] （1）

[εt=6hdtL2] （2）

[St=σ0εt] （3）

[Jt1St] （4）

[εs=ε2-ε1t2-t1/σ0] （5）

式中：[σ0]表示试件的蠕变弯拉应力，MPa；[εt]表示小梁试件梁底的弯拉应变；[St]表示试件的弯曲蠕变劲度模量，MPa；[Jt]表示试件的弯曲蠕变柔量，1/MPa；[εs]表示试件的弯曲蠕变速率，1/s/MPa；t1，t2表示蠕变稳定期直线段起始点及终点的时间，s；[ε1，ε2]表示分别对应于时间t1、t2时的蠕变应变；b表示跨中断面试件的宽度，mm；h表示跨中断面试件的高度，mm；L表示试件的跨径，mm；P0表示试件在试验加载过程中承受的荷载，N；[dt]表示试件加载过程中随时间t变化的跨中挠度，mm。

2 蠕变试验结果及分析

2.1 纤维体积率

2.1.1 蠕变变形。小梁弯曲蠕变试验采集到的纤维沥青混凝土在不同纤维体积率Vf下的跨中挠度及由跨中挠度计算出的梁底弯拉应变与时间的关系曲线见图2。

（a）挠度

从图2可以看出，不同纤维体积率的沥青混凝土的蠕变变形（挠度和应变）-时间曲线的位置随纤维体积率的增大先降低然后升高，当纤维体积率为0.35%时，蠕变变形-时间曲线处于图中的最下部位置。原因在于，合适体积率的纤维在沥青混凝土中均匀分散形成空间三维分布的纤维网格，纤维网格的加筋和桥接作用约束了沥青混凝土小梁在蠕变荷载作用下的变形，纤维对变形的约束阻滞作用又随纤维网格密度的增大而增强；当纤维的体积率达到0.35%，此时纤维网格具有最佳密度，沥青混凝土蠕变变形量最小，蠕变速率最低，纤维表现出较好的加筋和稳定的作用。当纤维体积率超过0.35%时，一方面，纤维因体积率过大而分散性降低，部分没有分散的纤维结团成束，挤开沥青混凝土中的集料，增大了沥青混凝土的孔隙率，并在沥青混凝土中形成新的缺陷；另一方面，过量的纤维因网格密度过大而形成局部纤维聚集，聚集的纤维成为纤维网格中的瑕点[14]。结团和聚集的纤维反而降低纤维的加筋和稳定作用，从而导致沥青混凝土蠕变变形量和蠕变速率缓慢增加，表现为当纤维体积率为0.52%和0.69%时，纤维沥青混凝土的蠕变变形-时间曲线位置上移。蠕变变形-时间曲线的位置反映了沥青混凝土抗蠕变变形性能，蠕变变形-时间曲线的位置越低，单位时间内的蠕变变形越小，蠕变速率越低，纤维对蠕变变形的约束能力就越强。当纤维体积率为0.35%时，聚酯纤维沥青混凝土蠕变变形-时间曲线在图中的位置最低，此时聚酯纤维沥青混凝土表现出较好的抗蠕变变形能力。

2.1.2 蠕变速率。蠕变速率是沥青混凝土小梁试件在单位应力条件下、单位时间内的应变变化。低温时，蠕变速率越大，沥青混凝土的变形能力越强，韧性越好，沥青混凝土就具有较好的低温抗裂性能；高温时，蠕变速率越小，沥青混凝土具有较好的抵抗荷载作用下的黏弹性变形能力[1]。根据不同体积率的纤维沥青混凝土蠕变试验结果，由式（5）计算的纤维沥青混凝土小梁在蠕变稳定期内的蠕变速率见表1。从表1可以看出，沥青混凝土稳定蠕变阶段，蠕变速率随纤维体积率的增大先减小然后增大，当纤维体积率为0.35%时蠕变速率最小，此时纤维表现出较好的蠕变变形约束能力。

2.1.3 蠕变柔量。蠕变柔量与蠕变劲度互为倒数关系，蠕变柔量越小，沥青混凝土材料抵抗蠕变变形的能力就越强。蠕变柔量-时间关系曲线位置越低，沥青混凝土抵抗蠕变变形的能力就越强。按式（4）计算的加载阶段不同纤维体积率条件下的沥青混凝土的蠕变柔量-时间关系见图3。

从图3可以看出，当纤维体积率为0.35%时，蠕变柔量-时间曲线处于图中的下部位置，此时纤维沥青混凝土表现出较好的抵抗蠕变变形能力。同时，蠕变柔量随时间变化的曲线具有明显的指数函数变化特征，函数表达式可以表示为：

[Jt=Btn] （6）

对不同纤维体积率的沥青混凝土加载阶段蠕变柔量进行指数函数回归分析，结果见表2。从表2可以看出，[B]随纤维体积率的增大先减小，然后增大的规律具有明显的二次曲线特征，可表示为：

[B=7.26×10-4-0.46Vf+119.3V2f] （7）

n随纤维体积率的增大而增大的变化规律具有明显的线性特征，可以表示为：

[n=0.422+0.28Vf R2=0.968 1] （8）

将式（7）和式（8）代入式（6）得到的考虑纤维体积率影响的纤维沥青混凝土蠕变柔量表达式，可表示为：

[Jt，Vf=7.29×10-4-0.002 7Vf+0.004V2ft0.422+0.28Vf] （9）

式（9）对[Vf]求导并令[Jt，Pf=0]，求解得到蠕变柔量取最小值时纤维体积率约为0.35%。

2.1.4 卸载回弹模量。沥青混凝土的卸载瞬时回弹模量是沥青混凝土抗蠕变变形能力和变形恢复能力的直接反映。利用卸载前后的蠕变试验结果可以计算出纤维沥青混凝土卸载瞬时回弹模量，计算公式为：

[ER=σ0Δε] （10）

式（10）中：[σ0]表示试验应力；[Δε]表示卸载前后应变差值。

不同纤维体积率的沥青混凝土卸载瞬时回弹模量见表3。从表3可以看出，纤维沥青混凝土的卸载瞬时回弹模量大于普通沥青混凝土，纤维增强了沥青混凝土的弹性；卸载瞬时回弹模量随纤维体积率的增大先增大然后减小，当纤维体积率为0.35%时，沥青混凝土的卸载瞬时回弹模量取得最大值。此时，沥青混凝土具有较好的蠕变荷载作用下的抗变形能力和卸载后弹性变形恢复能力[15]。

非线性回归纤维沥青混凝土卸载瞬时回弹模量随纤维体积率的增大先增大然后减小的变化关系，可表示为：

[ERVf=6 638.7+2 413.6Vf-3 6136.5V2f] （11）

2.2 纤维长径比

2.2.1 蠕变变形。不同纤维长径比的沥青混凝土小梁弯曲蠕变试验采集的跨中挠度及由跨中挠度计算的小梁跨中梁底弯拉应变与时间关系见图4。

（a） 挠度

从图4可以看出，蠕变变形-时间曲线的位置随纤维长径比的增大先降低然后升高。当纤维长径比为324时，蠕变变形-时间曲线位于图中的最下部位置，此时纤维沥青混凝土表现出较好的抵抗蠕变变形能力。原因在于，当纤维体积率、直径一定时，纤维长径比越大，单根纤维越长，软纤维的方向性越差，纤维就越易因卷曲而结团；纤维长径比越小，单位体积沥青混凝土内所含纤维的根数越多，纤维网格密度越大，纤维网格就越易于发生局部纤维聚集，从而降低了纤维的增强作用。当纤维长径比为324时，纤维不会因过长而卷曲，也不会因沥青混凝土内纤维网格密度过大而发生聚集，此时，纤维表现出较好的蠕变变形约束能力。由此可见，纤维沥青混凝土中的纤维存在一个最佳长径比。通过试验，本文得出聚酯纤维的最佳长径比为324。

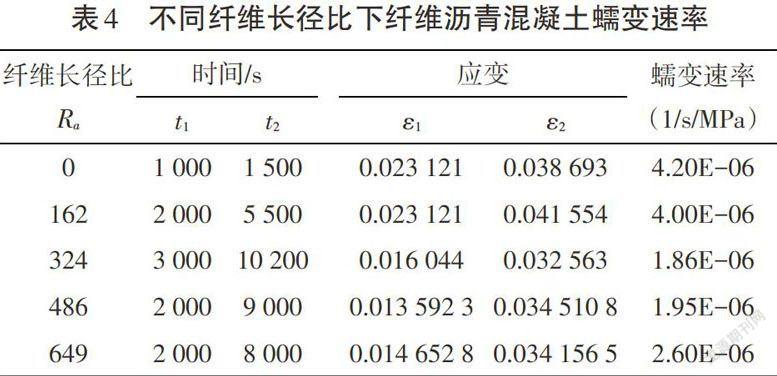
2.2.2 蠕变速率。由式（5）计算的不同纤维长径比的沥青混凝土小梁弯曲蠕变速率见表4。从表4可以看出，纤维沥青混凝土稳定蠕变阶段蠕变速率随纤维长径比的增大先减小然后增大，当纤维长径比为324时，蠕变速率最低，此时纤维表现出较好的蠕变变形约束能力。

2.2.3 蠕变柔量。按式（4）计算的不同纤维长径比的沥青混凝土加载阶段蠕变柔量随时间变化关系见图5。

从图5可以看出，蠕变柔量-时间曲线位置随纤维长径比的增大先降低然后升高。当纤维长径比为324时，蠕变柔量-时间关系曲线处于图中的最下部位置，蠕变柔量-时间曲线位置越低，相同荷载等级、相同荷载作用时间下，纤维沥青混凝土抵抗蠕变变形的能力就越强，此时，纤维沥青混凝土表现出较好的抵抗蠕变变形能力。

对不同纤维长径比的沥青混凝土蠕变加载阶段蠕变柔量随时间变化关系用式（6）进行指数函数回归分析，见表5。从图5可以看出，用指数函数拟合不同长径比的沥青混凝土加载阶段蠕变柔量与时间的关系具有较好的相关性。

蠕变柔量与时间的指数函数表达式中，B随纤维长径比的增大先减小后增大的规律具有明显的二次曲线特征，可表示为：

[B=6.78×10-4-2.8×10-6Ra+3.89×10-9R2a] （12）

蠕变柔量与时间的指数函数表达式中，n随纤维长径比的增大而增大的规律具有明显的线性特征，可以表示为：

[n=0.404+4.08×10-4Ra R2=0.991 9] （13）

将式（12）和式（13）代入式（6）可得考虑纤维长径比影响的纤维沥青混凝土蠕变柔量表达式，可表示为：

[Jt，Ra=6.78×10-4-2.8×10-6Ra+3.89×10-9R2at0.404+4.08×10-4Ra]（14）

由式（14）得出不同加载时间下蠕变柔量随纤维长径比变化的曲线见图6。

从图6可以看出，不同纤维长径比条件下，蠕变柔量随加载时间的增大而增大；同加载时间条件下，蠕变柔量随纤维长径比的增大先减小然后增大，当纤维长径比为324时取得最小值。

2.2.4 卸载瞬时回弹模量。按式（10）计算得出的不同纤维长径比的沥青混凝土的卸载瞬时回弹模量见表6。

从表6可以看出，由于纤维对沥青混凝土变形的约束，增强了沥青混凝土的弹性，不同长径比的纤维沥青混凝土卸载后的瞬时回弹模量大于普通基体沥青混凝土；纤维沥青混凝土的卸载瞬时回弹模量随纤维长径比的增

大先增大然后减小，当纤维长径比为324时，纤维沥青混凝土卸载瞬时回弹模量取得最大值，此时，纤维沥青混凝土具有较好的蠕变加载条件下的抗变形能力和卸载后蠕变变形恢复能力。非线性拟合纤维沥青混凝土卸载瞬时回弹模量随纤维长径比的增大先增大然后减小的变化规律可表示为：

[ERRa=6356.1+32.656Ra-0.0487R2a] （15）

综上所述，纤维体积率和长径比是影响沥青混凝土蠕变性能的重要因素，可以用纤维含量特征参数[λf=Vf×Ra]综合反映纤维体积率和长径比对沥青混凝土蠕变性能的影响。蠕变速率和蠕变柔量具有随纤维含量特征参数的增大先减小然后增大的变化规律，卸载瞬时回弹模量具有随纤维含量特征参数的增大先增大然后减小的变化规律，非线性拟合蠕变速率、蠕变柔量和卸载瞬时回弹模量与纤维含量特征参数的关系式可分别表示为：

蠕变速率：

[εsλf=4.41×10-6-3.6×10-6λf+1.35×10-6λ2f] （16）

蠕变柔量：

[Jt，λf=7.04×10-4-8.2×10-3λf+3.6×10-4λ2ft0.103+0.413λf]（17）

卸載瞬时回弹模量：

[ERλf=6 489.8+8 460.6λf-3 763.3λ2f] （18）

式（16）至式（18）分别对[λf]求导数，并令导数等于零，可得出蠕变速率和蠕变柔量取得最小值、卸载瞬时回弹模量取得最大值时的纤维含量特征参数值约为1.13。此时，纤维沥青混凝土表现出较好的抵抗蠕变变形和卸载后的弹性变形恢复能力。

3 结论

①纤维沥青混凝土蠕变变形-时间曲线、蠕变柔量-时间曲线的位置随纤维体积率和长径比的增大先降低然后升高。当纤维体积率为0.35%、长径比为324时，聚酯纤维沥青混凝土蠕变变形-时间曲线、蠕变柔量-时间曲线的位置最低。此时，聚酯纤维沥青混凝土表现出较好的抗蠕变变形能力。

②沥青混凝土稳定蠕变阶段蠕变速率随纤维体积率和长径比的增大先减小然后增大。当纤维体积率为0.35%、长径比为324时，蠕变速率最低。此时，纤维沥青混凝土表现出较好的蠕变变形约束能力。

③纤维沥青混凝土的卸载瞬时回弹模量随纤维体积率和长径比的增大先增大然后减小。当纤维体积率为0.35%、长径比为324时，沥青混凝土的卸载瞬时回弹模量取得最大值。此时，纤维沥青混凝土表现出较好的蠕变荷载作用下的抗变形能力和卸载后弹性变形恢复能力。

④纤维含量特征参数能综合反映纤维体积率和长径比的影响，当纤维含量特征参数为1.13时，纤维沥青混凝土表现出较好的抗变形能力和变形恢复能力。

參考文献：

[1]闵召晖，王晓，黄卫.环氧沥青混凝土的蠕变特性试验研究[J].公路交通科技，2004（1）：1-4.

[2]樊统江，何兆益.沥青混合料静态蠕变劲度模量与动稳定度的关系[J].重庆交通大学学报（自然科学版），2008（6）：1054-1057.

[3]孟庆龙.沥青混凝土小梁弯曲蠕变试验研究及ANSYS分析[D].长春：吉林大学，2005.

[4]杨挺青.粘弹性力学[M].武汉：华中理工大学出版社，1990.

[5]徐世法.表征沥青及沥青混合料高低温蠕变性能的流变学模型[J].力学与实践，1992（1）：37-40.

[6]叶永.沥青混合料粘弹塑本构模型的实验研究[D].武汉：华中科技大学，2009.

[7]张久鹏，徐丽，王秉刚.沥青混合料蠕变模型的改进及其参数确定[J].武汉理工大学学报（交通科学与工程版），2010（4）：699-706.

[8]郝培文，刘红英.运用蠕变速率评价沥青混合料低温抗裂性能研究[J].石油沥青，1994（3）：6-10.

[9]祈峰.采用蠕变性能试验评价沥青混合料高温稳定性研究[D].西安：长安大学，2009.

[10]王随原，周进川.SBS改性沥青混合料蠕变性能试验研究[J].公路交通科技，2006（12）：10-13.

[11]侯金成.纤维沥青混凝土粘弹性能研究[D].大连：大连海事大学，2007.

[12]Benedito de S. Bueno， Wander R. da Silva，Dario C. de Lima， Enivaldo Minete. Engineering properties of fiber reinforced cold asphalt mixes[J]. Journal of Environmental Engineering，2003（10）：952-955.

[13]郭乃胜，赵颖华，孙略伦.纤维沥青混凝土蠕变特性试验研究[J].中外公路，2007（2）：124-127.

[14]郭乃胜，赵颖华.纤维沥青混凝土粘弹性分析[J].交通运输工程学报，2007（5）：37-40.

[15]封基良.纤维沥青混合料增强机理及其性能研究[D].南京：东南大学，2007.

[16]中华人民共和国交通部.公路沥青路面施工技术规范：JTG F40—2004[S].北京：人民交通出版社，2004.

[17]中华人民共和国交通运输部.公路工程沥青及沥青混合料试验规程：JTG E20—2011[S].北京：人民交通出版社，2011.