超低频天线设计中的运动感应噪声研究

李春腾，蒋宇中，刘芳君，向 梅

(1.海军工程大学 电子工程学院，武汉 430033；2.云南民族大学 数学与计算机科学学院，昆明 650500；3.94826部队作战指挥中心信息支援室，上海 200433)

0 引 言

超低频通信在地-电离层波导内传播，频段为45 Hz时，每1 000 km的衰减大概在0.23 dB左右，这一点适合于远距离潜艇通信。目前，在超低频通信中，普遍采用电极对拖曳天线[1]，但当潜艇的航向垂直于地球大圆路径时，导致垂直天线轴向的来波不能收信。因此，在现有电极对天线的基础上加装磁场天线有利于解决上述不能收信的问题[2]。

超低频通信中存在的电磁噪声主要有热噪声、运动感应噪声、磁致伸缩噪声和巴克豪森噪声[3]。Burrows从理论出发，研究了上述提到的4种噪声源，并对环天线的振动进行实验测试[4]；文献[5]建立了拖曳天线在随机脉动压力下的横向振动模型，并得到相应的仿真结果；文献[6]对磁致伸缩噪声进行了建模及仿真分析。近年来，国内的研究大都基于文献[7]，基本上都是分析横向振动诱发电磁噪声的机理、天线长度和潜艇速度对噪声功率谱的影响以及在相同条件下对磁场和电场天线进行对比，尚未对影响噪声功率谱的横向力分布谱密度进行数据拟合及分析。本文建立了磁场天线的理想振动模型，导出天线灵敏度对运动感应噪声的影响，优化配置线圈的电磁结构，给出横向力分布谱密度的数据拟合，并在天线机械结构相同的情况下对上述的数据拟合结果进行对比分析。

1 磁场天线的理想振动模型统设计

对于磁场天线而言，由于穿过线圈的磁通量改变而产生运动感应噪声。假定磁场天线的部分机械结构理想化(主要指弯曲硬度、电缆浮力等结构)，建立的磁场天线理想振动模型如图1所示。

图1 磁场天线理想振动模型Fig.1 Ideal vibration model of H-field antenna

磁场天线的长度为2l，磁芯半径为r，线圈的半径为a，天线的轴线为z，通过天线所受的横向激励f(z,t)，得到的动力学方程为

(1)

(1)式中：EI代表天线的弯曲硬度，在此理想模型下，为一固定值；T代表天线张力，将其视为均匀分布；mt代表天线横向振动的有效质量[7]；y(z,t)代表天线中心线在轴线上的横向位移；当研究天线上某点(以z1为例)的横向激励时，可将f(z,t)用冲激函数表示，即

f(z,t)=f1(t)δ(z-z1)

(2)

结合(1)—(2)式，并将其转换成频域中，可得

Y1(k,w)=Ht(k,w)F1(w)e-ikz1

(3)

(3)式中：Y1(k,w)代表天线某点横向位移的功率谱密度；F1(w)表示横向激励的功率谱；Ht(k,w)相当于传递函数，具体表达式为

(4)

2 不同天线灵敏度的运动感应噪声分析

目前，天线设计中，灵敏度曲线形式一般选择主流的抛物线型，即让天线两端的灵敏度为0，而中间部分采用抛物线型产生最佳的等效噪声场。但并未详细给出均匀灵敏度天线运动感应噪声功率谱的表达式，也未给出如何在实际环境中实现抛物线型灵敏度。

通过文献[8]可知，均匀灵敏度天线的运动感应电压为

(5)

(5)式中：By代表y方向上的磁感应强度；u1代表天线的均匀灵敏度，主要与天线的线圈面积、天线的匝数密度以及天线的相对导磁率有关。

在频域中，仅考虑l端的运动感应电压，则(5)式可表示为

V1(w)=-iwByu1Y1(k,w)

(6)

结合(3)式和(6)式，则l端产生的运动感应噪声电压总的功率谱密度为

(7)

(7)式中，Sf(k,w)代表横向激励F1(w)的谱密度。

假设横向激励分布均匀且统计独立，并且Sf(k,w)在Ht(k,w)幅值较大的区域相对平坦，则可用Sf(0,w)来近似代替Sf(k,w)，故(7)式可转化为

(8)

(9)

同理，得到-l端的Se(w)与此相同，故均匀灵敏度天线总的功率谱密度为2Se(w)。为便于与抛物线型灵敏度作比较，引入2个参数：横向波传播的特性波数kt和天线的机械品质因数Qt。Qt定义为

(10)

由(4)式可得

(11)

结合(9)—(11)式，最终得到功率谱密度为

(12)

由此可得到均匀灵敏度天线比抛物线型天线多诱发ktQtl/3π倍的噪声，通过文献[7]可以得到kt，Qt与张力T和频率之间的关系曲线，得到不同天线长度下2种灵敏度类型诱发的噪声，如表1所示，选取T为1 000 N。

通过数据对比可以发现，均匀灵敏度和抛物线型天线在不同频率和天线长度下诱发的噪声强度不同，但均匀灵敏度型天线诱发的噪声始终要多于抛物线型。以频率为120 Hz为例加以说明，在天线长度为50 m时约为36.5 dB，长度为150 m时约为41.3 dB，长度为300 m时约为44.3 dB，这与主流的学术观点相符。因此，在实际天线设计中，首选抛物线型灵敏度天线。

由于天线的灵敏度主要与天线的线圈面积、天线的匝数密度以及天线的相对导磁率有关，因此，可以从以上3个方面着手，使天线的灵敏度分布为抛物线型。为简单实用起见，仅改变其中某一个参量：①通过增减铁磁合金使横截面积呈抛物线型；②通过编程控制电路平滑改变绕线匝距，使线圈匝密度呈抛物线型；③改变铁磁材料的磁导率使其呈抛物线型。方法①在设计时要求铁磁材料与内芯轴向平行，不适用于螺旋的铁磁合金，方法③基本无法实现。因此，总的来看只有方法②符合实际设计要求。

表1 均匀和抛物线型灵敏度天线诱发的噪声

3 横向力分布谱密度的数据拟合

(12)式和抛物线型天线的噪声功率谱密度表明，噪声功率谱密度与横向力分布谱密度有重要联系。由于Bakewell在实验中仅给出实验数据[9]，而没有给出严格的横向力分布谱密度函数，因此，本文利用获取的Bakewell实验数据进行拟合，并将拟合结果与目前普遍采用的公式在相同天线长度和潜艇速度的条件下比较分析。

Burrows在文献[7]中近似给出了二维谱密度公式为

(13)

(13)式中：φ(w)为Bakewell实验中定义的与扰动声压有关的变量；uc为频率w的对流速度。

通过(13)式可知，其中包含φ(w)，uc2个函数。Bakewell在文献中提供了关于上述2个函数的实验数据，但由于对uc函数提供的数据量过少(仅有10个点)，并且在实验数据提取的过程中会不可避免地引入误差，因此，对于uc函数，本文采用目前的主流函数，仅对数据足够多的φ(w)函数进行数据拟合，φ(w)函数的数据拟合结果如图2所示。从图2a提取的Bakewell数据来看，最可能与之相关的就是指数函数和多项式分布，因此，仅使用这2种函数对数据拟合。

图2 φ(w)函数的数据拟合结果Fig.2 Results of data fitting about function φ(w)

目前φ(w)函数的主流思想是指数函数，为验证这一点，本文分别采用指数函数和二次多项式进行数据拟合，并将拟合的结果呈现在图2b中，图2c为指数拟合曲线的表达式及误差，图2d为二次多项式拟合曲线的表达式及误差。

指数拟合得到的表达式为

(14)

二次多项式拟合得到的表达式为

(15)

4 运动感应噪声仿真分析

图3中的仿真曲线表明，仅天线长度不同而其他参量相同的情况下，运动感应噪声谱密度随着天线长度的增加而降低；仅潜艇速度不同而其他参量相同的情况下，运动感应噪声谱密度随着潜艇速度的加快而增大；这与主流的学术观点是相同的。就数据拟合而言，指数函数与文献[10]中的运动感应噪声谱密度近乎相同，比文献[11]稍好；而多项式拟合要优于指数拟合方式，使噪声谱密度降低近26 dB。

将文中得到的仿真结果与文献[12]进行比较，两者的实验仿真参数基本一致，本文算法在航速为20，频率为50 Hz，在指数拟合的情况下得到的噪声功率谱密度为-210 dB，而文献[12]在航速为15，频率为50 Hz时，得到的噪声功率谱密度仅为-200 dB，本文在航速高于文献[12]的情况下，还能获得10 dB的优势，因此，本文算法明显优于文献[12]。若采用多项式拟合方式，其噪声功率谱密度大概为-235 dB，会使噪声谱密度降低近35 dB。

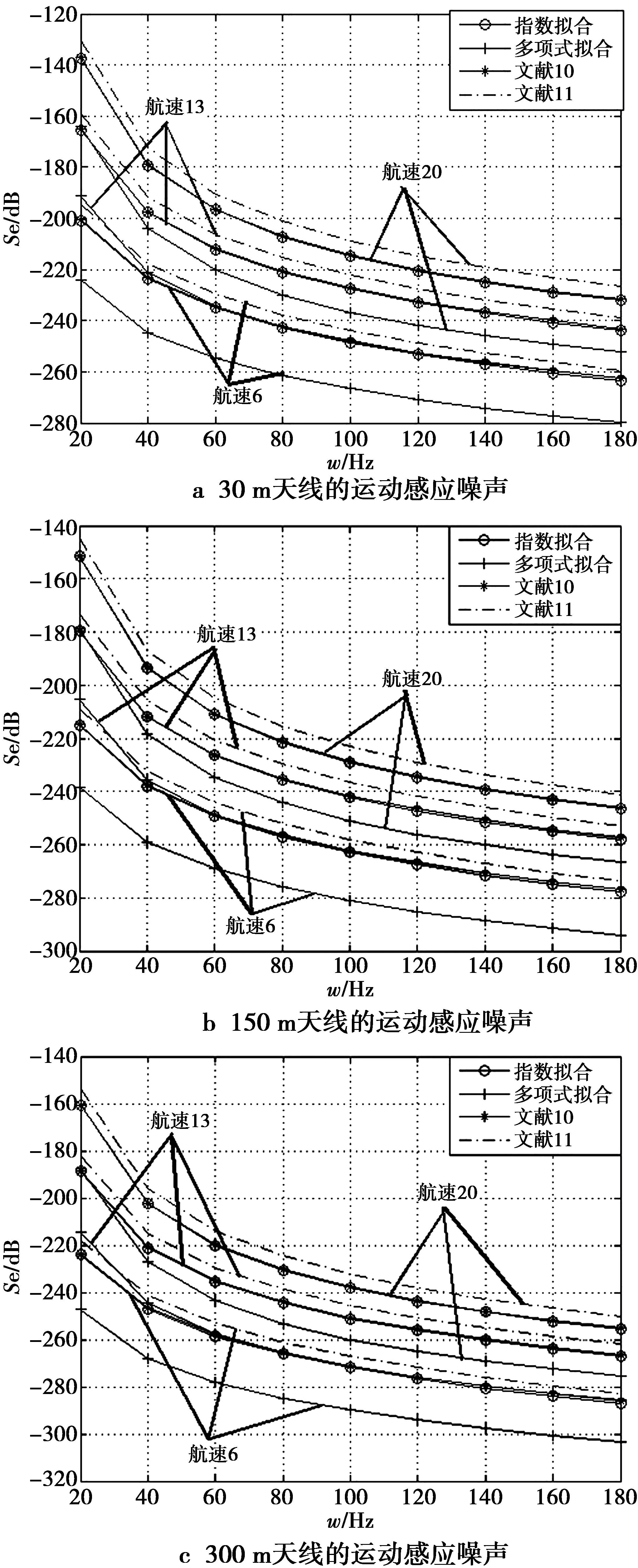
图3 不同天线长度的运动感应噪声Fig.3 Motion-induced noise of different antenna length

目前，虽然多项式拟合方式尚未被采用，分析其原因可能是多项式拟合方式不能很好地诠释物理含义，也无法表示φ(w)函数整体下降的趋势，只是局限在某一范围内使得噪声谱密度降低。但就Bakewell实验数据的拟合方式而言，多项式拟合确实要优于指数拟合。

5 结 论

本文建立了磁场天线的理想振动模型，对比了均匀和抛物线型灵敏度天线对运动感应噪声的影响，研究结果表明，在不同频率和天线长度下诱发的噪声强度不同，但均匀灵敏度型天线诱发的噪声始终要多于抛物线型，约40 dB。给出了实际构造抛物线型灵敏度天线的方法，为优化磁场天线的设计奠定基础。分别采用指数和多项式拟合方式对二维横向力分布函数进行拟合，拟合结果表明，本文提出的拟合方式在不同天线长度和不同潜艇航速下得到的噪声谱密度结果与主流的学术观点相同。指数拟合方式的性能略优于文献[10]和文献[11]，明显优于文献[12]，而多项式拟合方式优于指数拟合，能够使噪声谱密度降低近26 dB。虽然多项式拟合方式无法表示整体趋势，但在某一范围内该拟合方式确实能降低噪声谱密度。本文的研究结果为进一步研究运动感应噪声提供一定的基础。