孔式喷嘴油束碎裂的线性稳定性理论研究

曹建明 侯婕

(长安大学 汽车学院, 西安 710064)

引言

喷嘴喷射出的实心液柱称为液体圆射流,如孔式喷嘴的喷雾,它是车辆、航空航天等载运工具以及锅炉燃烧室中喷雾的主要形式之一.圆射流碎裂过程的理论研究是发动机喷雾研究的重要环节,是国际流体与燃烧学界的热点研究课题[1].目前,国际上对圆射流碎裂过程的理论研究多采用线性稳定性理论.线性稳定性理论是以气、液体质量、动量守恒为基础,代入边界条件,考虑到气液体速度、密度、气体可压缩性及液体的表面张力和粘性影响,从而得到色散关系式.该理论的核心和关键点就在于色散关系式的推导.色散关系式的推导要求研究者具有扎实的流体力学和数学知识,对各种边界条件的正确确定和数学推导的严密性要求很高,有时甚至需要反复研讨才会有所进展.当圆射流以连续液体的形式从喷嘴喷出时,受外界气体的扰动作用,在其表面会形成一定模式的表面波.从喷雾液束的形态来看,有截面呈圆形的单股状圆射流,也有像由二股、三股、甚至多股细绳扭转在一起而形成的一股粗绳状.阶数n=0的表面波对应于单股状对称波形的圆射流,阶数n=1的表面波对应单股状非对称波形的圆射流,阶数n=2、3、4…时的表面波对应二股状、三股状和四股状的圆射流,其中二股状和四股状圆射流为对称表面波形,三股状圆射流为非对称波形.早期,Reitz等人推导出了粘性圆射流喷射进入不可压缩气流中零阶色散关系式[2],此关系式被大型发动机工作过程数值计算程序KIVA中的圆射流碎裂模型所采用,该程序被国内外许多名牌大学和研究机构广泛使用,是目前国内各高校和研究机构培养发动机工作过程方向博士研究生的重要研究工具之一.1999年,Li推导出了粘性圆射流喷射进入不可压缩气流中零阶色散关系式及n阶色散关系式[3],据作者所知，此后国际上再也没有这方面的进一步研究发表.经作者推导比较,由于Reitz和Li所采用的线性运动学边界条件不同,Reitz的运动学边界条件简化得更多,使得二式略有差别.如果Reitz采用了Li的运动学边界条件或者Li采用了Reitz的运动学边界条件,则以上两个色散关系式完全相同.2010年,作者推导出了粘性圆射流喷射进入不可压缩气流中零阶量纲一色散准则关系式[4].

(1)

其中:k为表面波数；Eul为液体欧拉数；I0、I1分别为第一类0阶、1阶修正贝塞尔函数；ω为圆频率,其实部ωr为表面波增长率；Rel为液体雷诺数；s2=k2+Rel(ω+ik)；P为气液压力比；γ为绝热指数；Mag为气体马赫数；K0、K1分别为第二类0阶、1阶修正贝塞尔函数；U为气液流速比；Wel为液相韦伯数.

由于Reitz和Li的推导均采用了有量纲形式的控制方程和边界条件,其色散关系式也是有量纲形式的,经过推导,如果将Li等人的零阶色散关系式量纲一化,则与作者的零阶量纲一色散准则关系式是一致的.

n阶色散关系式比零阶色散关系式适用的范围更广,我们可以对阶数n选取不同的数值来研究圆射流的多种形态的表面波,可以说n阶色散关系式将圆射流的线性稳定性分析推导到了极致.但是由于Li对n阶色散关系式的推导采用了有量纲形式的控制方程和边界条件,因此其色散关系式也是有量纲形式的.这样一来,在根据他的色散关系式编制数值计算程序而得到的分析结果中,仅能够分析维伯数We、气液流速比、液体粘性和气体马赫数Ma等因素对圆射流碎裂过程的影响.根据相似理论,量纲一的准则关系式要比有量纲形式的关系式包含更多的信息量,适用范围更广,具有更大的优越性.本文从质量守恒和动量守恒的最原始方程式入手,首先推导出了液、气相的线性化纳维斯托克斯量纲一控制方程组,再将线性运动学和动力学边界条件量纲一化,进而推导出了n阶量纲一形式色散准则关系式,能够分析多种形态表面波的维伯数We、雷诺数Re、欧拉数Eu、气体马赫数Ma、气液流速比、气液压力比等诸多因素对圆射流碎裂过程的影响.

1 模型的建立

图1所示为圆射流表面波的示意图,图中参数已经量纲一化.考虑一个三维圆柱射流,初始半径为1,密度为ρl,以压力Pl,速度Ul,喷射进入密度为ρg,压力为Pg,速度为Ug的气体介质中.

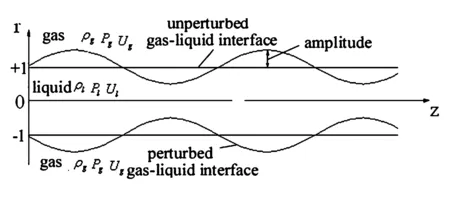
图1 圆射流表面波Fig.1 Surface wave of circular liquid jet

液流被看作是牛顿流体,并且质量力忽略不计,这是由于对于实际的喷雾应用来说Froude数是非常大的.液流经扰动后,合流参数值为:

ui,tot=Ui+ui,pi,tot=Pi+pi

其中:ui=(ur,uθ,uz)i,pi=pi(r,θ,z)分别指扰动速度和扰动压力,基流速度和基流压力为Ui=(Ur,Uθ,Uz)i=(0,0,1)i=const,Pl=Pl(0,0,1)=const.下标i=l代表液相,i=g代表气相.在动量守恒控制方程中,可将扰动速度项线性化.下标r,θ,z代表柱坐标(r,θ,z).

线性化的量纲一纳维-斯托克斯控制方程组,其形式如下:

液相、气相连续性方程:

(2)

液相动量方程:

(3)

气相动量方程:

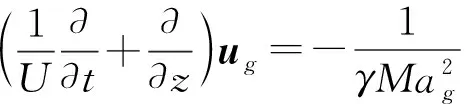
(4)

方程中的量纲一参数为液体欧拉数Eul,液体雷诺数Rei,气体马赫数Mag,气液流速比U和绝热指数γ.

量纲一纳维-斯托克斯控制方程组(2)～(4)的解必须满足流动运动学边界条件和流动动力学边界条件.在线性稳定性理论中,我们采用气液交界面处,即r=1时的线性化的边界条件.液相和气相的量纲一运动学边界条件方程分别表示为:

(5)

和

(6)

液相和气相的量纲一附加边界条件和动力学边界条件方程为：

(7)

(8)

(9)

(10)

2 液相推导

(11)

(12)

令:

pi=pi(r)exp(ωt+ikz+inθ)

(13)

ui=ui(r)exp(ωt+ikz+inθ)

(14)

将方程(13)代入方程(11)得:

(15)

方程(15)为n阶修正贝塞尔方程,其解为:

pl(r)=a1In(kr)+a2Kn(kr)

(16)

其中:In和Kn分别为第一类和第二类n阶修正贝塞尔函数.

将方程(16)代入方程(3),得:

r-方向动量方程:

(17)

θ-方向动量方程:

(18)

z-方向动量方程:

RelEulik[a1In(kr)+a2Kn(kr)]

(19)

其中:

s2=k2+Rel(ω+ik)

(20)

方程(17)、(18)、(19)的通解分别为:

(21)

(22)

ul,z(r)=c1In(sr)+c3Kn(sr)+c2In(kr)+c4Kn(kr)

(23)

其中:b1,b2,b3,b4,b5,b6；c1,c2,c3,c4；d1,d2,d3,d4,d5,d6为积分常数,且具有以下关系:

由于在圆柱中心线上r方向速度分量等于零,根据In、Kn曲线图(图2所示)可知,作为边界条件,当r→0 时,Kn→∞,因此,有a2=0,b4=0,b5=0,b6=0,c3=0,c4=0,d4=0,d5=0,d6=0.

图2 第一类、第二类修正贝塞尔函数 In、Kn曲线图Fig.2 1st and 2nd order modified Bessel functions In and Kn

方程(17)、(18)、(19)的通解变成:

(24)

(25)

(26)

将方程(24)、(25)、(26)代入方程(14),再代入运动学边界条件方程和动力学边界条件方程(5)和(7)、(8)、(9),并将圆射流的量纲一初始半径r=1代入,可得到积分常数a1,b1,c1和d1的解:

将方程(16)和a1,b1,c1,d1代入方程(13),得液相压力为:

(27)

3 气相推导

将方程(13)代入方程(11)得:

(28)

方程(28)为n阶修正贝塞尔方程,其解为:

pg(r)=e1In(kr)+e2Kn(kr)

(29)

将方程(29)代入方程(4)得:

r-方向动量方程:

(30)

由于在r→∞方向上气流的速度分量等于零,根据In、Kn曲线图(图2所示)可知,作为边界条件,当r→∞时,In→∞,因此,e1=0.

根据与液相推导相同的步骤,可以得到气相的积分常数e2的解:

和气相压力:

(31)

4 量纲一色散准则关系式

将方程(27)和方程(31)代入动力学边界条件方程(10),可得到n阶量纲一色散准则方程式:

(32)

经过验证,当n=0时,方程(32)变成:

(33)

由于:

方程(33)变成:

(34)

显然,方程(34)与之前推导的零阶量纲一色散准则方程式(1)是一致的,也可以说是与Reitz和Li等人的零阶色散关系式是一致的,从而说明了推导出的n阶量纲一色散准则方程式(32)的正确性.从方程(32)我们还可以看出,n阶量纲一色散准则方程只与量纲一参数:维伯数We、雷诺数Re、欧拉数Eu、马赫数Ma、气液流速比U、气液压力比P等有关.

5 结论

本文从质量守恒和动量守恒的最原始方程式入手,首先推导出了液、气相的线性化纳维斯托克斯量纲一控制方程组,再将线性运动学和动力学边界条件量纲一化,采用对动量方程点乘哈密顿算子的方法,推导出了粘性圆射流喷射进入不可压缩气流中的n阶量纲一色散准则关系式.结论如下:

(1)对于n阶量纲一色散准则关系式,将n取不同的值,可以得到圆射流不同形态表面波的量纲一色散准则关系式,其适用范围更广,具有更大的优越性.

(2)n阶量纲一色散准则方程式只与无量纲参数——韦伯准则We、欧拉准则Eu、雷诺准则Re、气体马赫准则Mag、气液流速比U及气液压力比P有关.经过编程和数值计算,可以得到这些量纲一参数对圆射流碎裂过程的影响.