基于捷联惯导姿态的外测跟踪部位修正方法

2018-09-07胡长城李松军李斌杨博姚尚

动力学与控制学报 2018年4期

胡长城李松军李斌杨博姚尚

(甘肃酒泉十四支局565号, 酒泉 735018)

引言

在外测数据事后处理过程中,跟踪部位修正是经常必做的一个重要环节,通常是基于以下两种考虑：一是在外测过程中有多种、多台设备同时进行测量,这些测量设备所对应的目标跟踪点(简称跟踪部位)往往是不同的,在事后处理中为了进行数据综合处理,要把测量结果数据归算到统一部位上[1]；二是外测光学设备脱靶量数据的处理是基于目标图像几何特征点的,而目标试验结果分析、评定是基于目标战斗部的,为了有效进行目标战斗部指标的分析评定,要把数据处理基准点从特征点位置修正到目标的战斗部位置上.数据处理中为了实现目标的跟踪部位修正,采用测元修正法或位置参数修正法对目标数据进行修正[2].测元修正法要求明确知道处理点和待修正点的坐标,如大地坐标,可以通过坐标反算测元差,对测量设备的测元进行修正；对于只知道处理基准点和待修正点相对几何位置的情况,则需要用位置参数修正法进行修正.位置参数修正中涉及的一个重要参数就是目标的姿态参数,由于测试条件限制,通常由航迹偏角、航迹倾角代替近似计算,使用速度矢量修正法进行修正,精度受到限制.近年来,由于捷联惯导系统反应时间短、可靠性高、体积小、重量轻、成本逐步下降等突出优点,在空空武器中得到了广泛应用[3],惯导精度也逐渐提高,快速传递对准能够达到1毫弧度以下的姿态误差[4],外测数据处理能够从中获取较为准确的目标飞行姿态参数.本文基于捷联惯导的姿态信息提出一种新的跟踪误差修正方法,利用捷联惯导系统姿态旋转矩阵信息,依据外测数据处理中各个参照坐标系的相互关系,修正了垂线偏差的影响,推导外测数据事后处理跟踪部位修正方法,实现外测数据事后处理跟踪部位位置参数修正,并与常用的速度矢量修正法进行比较,验证修正方法的正确性,达到外测事后数据处理的精度要求.

1 基于捷联惯导系统姿态参数修正方法

1.1 坐标系定义

基于捷联惯导系统姿态参数修正方法涉及的坐标系包括以下几种[5]：

(1)大地直角坐标系Od-xdydzd,原点o为地球质心,z轴指向IERS参考极(IRP)方向,x轴指向IERS参考子午面与通过原点且同z轴正交的赤道面的交线,y轴与z轴、x轴构成右手坐标系.

(2)地心惯性坐标系Oc-xcyczc,实际工作中为了处理方便,通常取目标发射瞬间的大地直角坐标系作为地心惯性坐标系,此时其三轴指向不再随地

球的自转而发生变化.

(3)发射惯性坐标系Of-xfyfzf,目标发射瞬间的发射坐标系.该发射坐标系的原点为目标质心在当地海平面上的投影点,x轴指向天文北,y轴与过投影点的铅垂线一致,指向外,z轴与x轴、y轴构成右手坐标系,此时其三轴指向不再随地球的自转而发生变化.

(4)数据处理坐标系Ob-xbybzb,原点O选取航区某测量设备的三轴(水平轴、垂直轴、照准轴)交点,也可为指定的某点；OX轴指向大地北；OY轴与地球椭球体上过原点的法线重合,指向外；OZ轴与OX、OY构成右手直角坐标系.

(5)体坐标系Obm-xbmybmzbm,原点O为飞行器质心或某一特征点,OX轴与飞行器的纵轴方向一致,向前为正；OY轴位于飞行器的竖对称平面内,垂直于OX轴,向上为正；OZ轴与OX、OY构成右手直角坐标系.

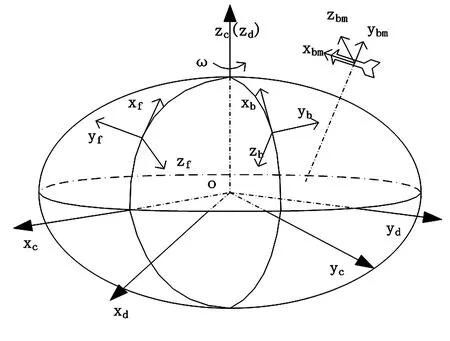
图1 坐标系示意图Fig.1 Diagrammatic sketch of coordinate systems

1.2 垂线系到法线系转换的垂线偏差修正

垂线坐标系的基准面是水平面,法线坐标系的基准面是椭球面,无论是参考椭球还是总的地球椭球．其表面都不可能与大地水准面处处重合,因而在同一测站点上铅垂线与椭球面法线也不会重合.两者之间的夹角u称为垂线偏差,在坐标转换时会引起误差.垂线偏差的大小和方向随着点位不同发生不规则的变化.垂线偏差u常用南北方向上的子午投影分量ξ和东西方向上的投影卯酉分量η来表示,则垂线偏差修正矩阵可表示为[6]：

(1)

因垂线和法线差异带来的北向差异可由下式求出[7]：

Δγ=α-A=(λ-L)sinφ+(ξsinA-ηcosA)ctgZt

(2)

式中α为天文方位角,A为大地方位角,λ,φ为天文经纬度,Zt为天顶距,右端第一项只与点的位置有关,与照准点的方位及天顶距无关；第二项与照准点的方位及天顶距有关.在通常情况下,由于垂线偏差一般小于10″,当Zt=90°时,第三项为百分之几秒,故此项略去,得到简化公式Δγ=(λ-L)sinφ,又因为：

η=(λ-L)cosφ,B=φ-ξ

则：α-A=ηtanφ=ηtan(B+ξ)≈ηtanB

则把坐标绕y轴旋转Δγ,则最终旋转矩阵为：

(3)

由于小角度的正弦约等于自身,余弦约等于1,上式可变为：

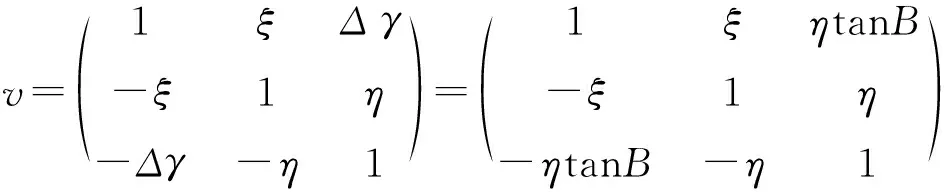
(4)

1.3 发射惯性系到数据处理坐标系

从坐标系的定义和欧拉法[8]可以得出地心大地坐标系和数据处理坐标系的关系为：

(5)

(6)

其中e为第一偏心率,Bb0c、Lb0c为原点经纬度和高,Rx,Ry,Rz称为旋转矩阵,以下同上.

(7)

地心大地坐标系和地心惯性坐标系的坐标关系为：

(8)

其中：ω=7.292115×10-5rad/s为地球旋转角速度[9],t为从选定时刻开始的飞行时间.发射惯性坐标系和地心惯性坐标系关系为：

(9)

(10)

发射系原点坐标计算公式同数据处理坐标系原点计算.体坐标系和发射惯性坐标系的关系为：

(11)

(12)

式中φ、ψ、γ为姿态角,综合以上(4)、(6)、(8)、(10)、(12)可得体坐标系到数据处理坐标系转换关系为：

(13)

其中xbm,ybm,zbm为体坐标系坐标,xfm0,yfm0,zfm0为体坐标系原点在发射系下的坐标.则同时刻目标从一个部位b1修正到另一个部位b2的坐标修正量可表示为：

(14)

(15)

由于实际工作中,四元数法与欧拉角法相比,计算量小、精度高、可避免奇异性,捷联惯导应用中多采用四元数法,根据欧拉角和四元素的关系,旋转矩阵C4可用四元数表示的捷联矩阵表示[10]：

(16)

2 跟踪部位速度矢量位置量修正方法

在外弹道数据处理中,由于测试条件和目标本身等原因限制,经常缺少姿态数据.但为满足处理数据和分析数据的需要,需进行跟踪处理部位修正.这种情况下,通常采用目标飞行的航迹偏角、航迹倾角数据,采用速度矢量法进行位置修正[11].

(1)弹的位置修正量

(17)

其中L为跟踪部位到处理部位修正的长度,如弹长等.vm,vmx,vmy,vmz为导弹速度和分量,速度亦可以是处理区间内的平均速度及分量.

(2)靶机的位置修正量

(18)

L1为目标跟踪部位中心至目标处理部位的轴向距离,顺航线修正为正,L2为目标跟踪部位中心至目标处理部位的展向距离,顺航线左修为正,L3为目标跟踪部位中心至目标处理部位所在平面的法向距离,向上为正.vt,vtx,vty,vtz为导弹速度和分量,速度亦可以是处理区间内的平均速度及分量.γ为倾斜角,顺行右滚为正.

速度矢量修正方法是对速度进行微分处理计算得到,精度较差,属于近似修正,基于捷联惯导姿态的修正方法是对目标在空中的姿态参数进行修正,属于高精度修正.

3 数据仿真分析

以某型导弹目标飞行数据为例,按照真实状态,仿真飞行位置、速度、姿态等数据,把处理部位从弹尾修正到战斗部.分别用上述两种方法进行计算,验证基于捷联惯导系统姿态参数的跟踪部位修正方法的修正效果.图2为使用基于捷联惯导系统姿态参数跟踪部位修正方法修正的结果随时间变化曲线.

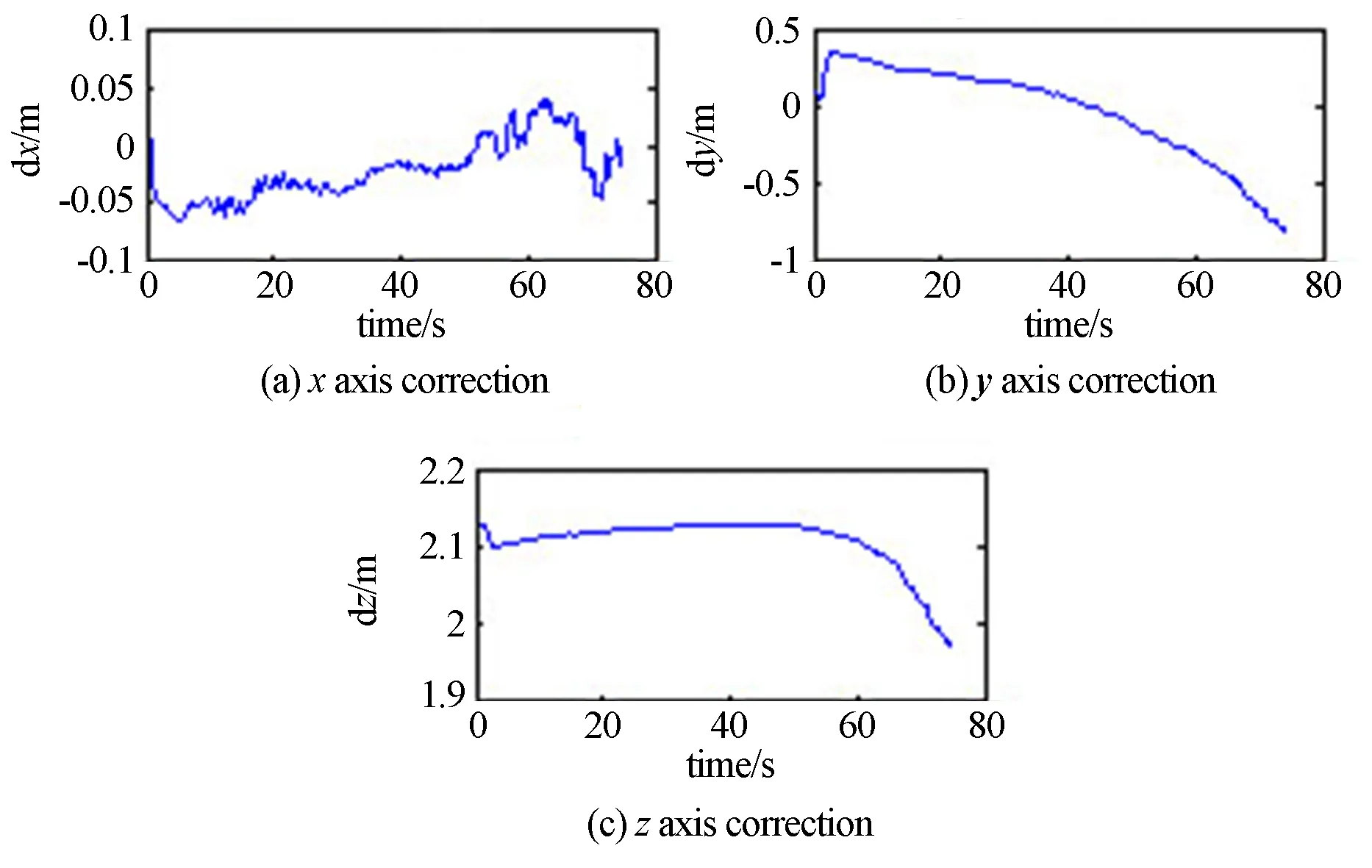
图2 基于捷联惯导系统姿态参数修正结果Fig.2 Correction results based on attitude of the strapdown inertial navigation system

从图2可以看出,修正量主要体现在目标运动的主方向z上,由于目标具有一定的飞行倾角,y向上产生一定小的分量,在侧向x方向数值很小,可忽略,不需要进行修正,与实际飞行设定情况基本相一致.图3为用捷联惯导系统姿态参数与速度矢量修正两种方法修正比对结果随时间的变化情况.表1为两者比对结果的统计值.

图3 捷联惯导系统姿态参数与速度矢量修正差值Fig.3 Difference of attitude correction and velocity vector correction

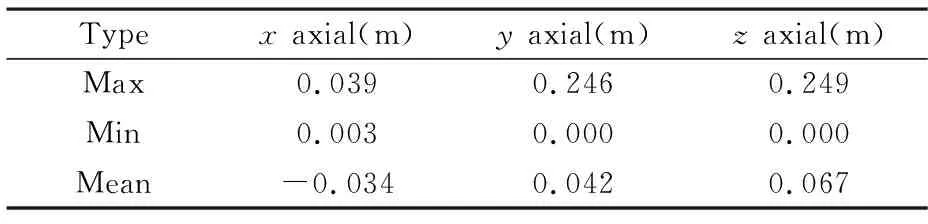
Typex axial(m)y axial(m)z axial(m)Max0.0390.2460.249Min0.0030.0000.000Mean-0.0340.0420.067

从图3和表1可以看出三个方向两者修正结果,以z向为例,最大值为0.249m,最小值为0m,平均为0.067m,满足常规弹道修正精度要求,两者结果一致.这说明经过处理后的捷联惯导姿态数据的精度可以满足跟踪误差修正的精度要求,进一步验证了本文修正方法的可行性和正确性,事实上空空武器弹体较小,跟踪位置修正对姿态精度要求不是十分严苛.另一方面对于高精度脱靶量处理要求来讲,通常0.5m左右的差异就会影响到武器毁伤效果的评估,尤其是在边界条件情况下.随着目标俯仰角的增大,用航迹倾角近似俯仰角的误差将增大,速度矢量修正作为一种近似修正,修正误差变大,仿真数据验证结果说明速度矢量修正的应用具有一定局限性.通过严格的公式推导,采用基于捷联惯导姿态修正方法可以保证修正结果的正确性,也与实际应用相一致.图4中(a)、(b)、(c) 为合修正量随姿态角变化情况,图4中(d)为弹道倾角与姿态俯仰角差值随时间的变化情况.表2为合修正量差随姿态俯仰角和弹道倾角差值变化的统计分析结果.

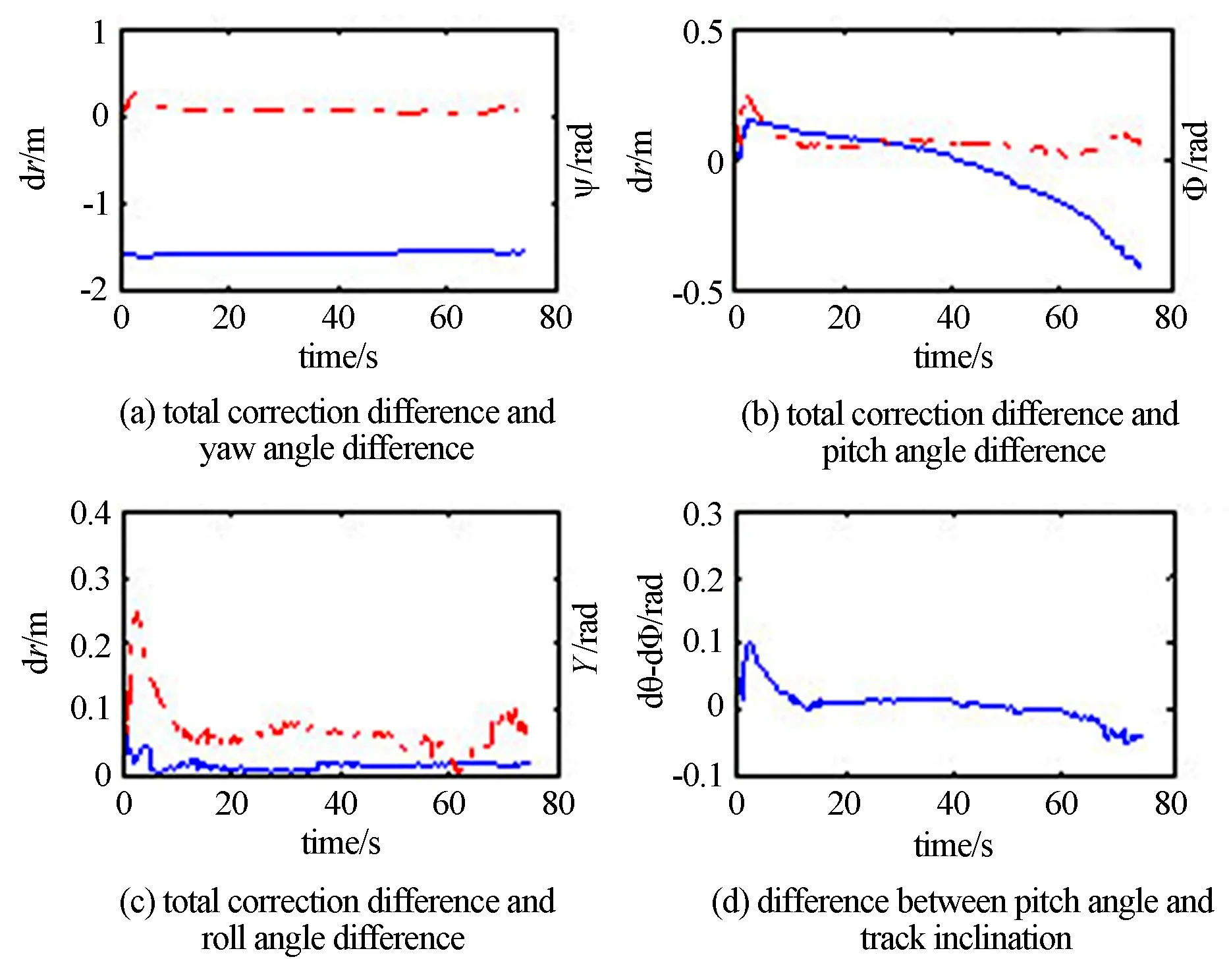
图4 修正量随姿态角度的变化Fig.4 Correctionvalues with the change of attitude

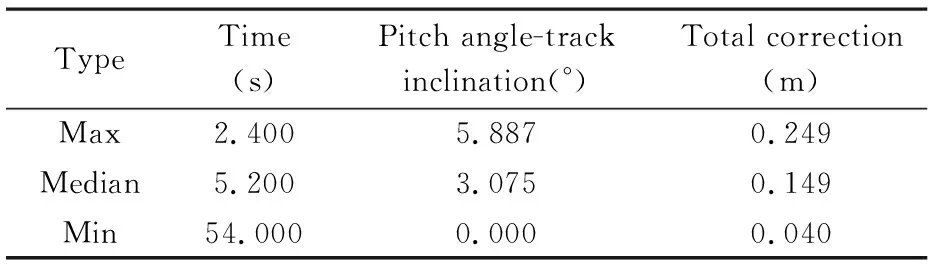
TypeTime(s)Pitch angle-track inclination(°)Total correction(m)Max2.4005.8870.249Median5.2003.0750.149Min 54.0000.0000.040

从图4可以看出,两种修正算法之间的差异随着目标的弹道倾角、偏角和目标的姿态角之间的差异而变化.以倾角为例,见图3(d)、图4(d)、表1和表2,随着两者之间的差变大,两者修正的结果差异也变大,在2.4s最大,对应y修正量值最大为0.246m,在54s最小,对应y修正量最小值为0m.按照修正量误差控制在脱靶量处理精度1/3的量值来算,单向修正量应控制在0.15m,对应姿态俯仰角度和弹道倾角差约为3°,说明当姿态角三个方向平均差异在3°以上时,在做脱靶量处理时会影响数据处理精度,严重时会影响目标的杀伤效果评定,此时应采取基于捷联惯导系统的姿态修正方法进行目标部位修正.在实际应用中,捷联惯性组合初始对准精度较高,且短时间内变化较小,加上惯导系统具有自修正手段,因此,初始对准误差对捷联惯导姿态修正方法的精度影响较小.