变截面旋转叶片的非线性动力学研究*

张伟 袁双 郭翔鹰

(北京工业大学 机电学院, 北京 100124)

引言

叶片是航空发动机的关键零部件之一,在工作中起着转换能量的作用,被称为发动机的心脏,其质量好坏直接影响了发动机的工作效率和运行的可靠性.航空发动机叶片工作环境恶劣,在高速旋转运动中承受着气动力、离心力的作用,由此而产生的振动对发动机的性能、耐久性、可靠性和寿命具有非常大的影响.发动机中压气机叶片需要完成对气体的压缩和膨胀,并且以最高的效率产生强大的动力来推动飞机前进的工作.而叶片作为一种特殊的零件,它数量多,形状复杂,要求高,加工难度大,而且是故障多发的零件,一直以来是各发动机厂生产的关键,因此发动机叶片的研究极为重要.

目前,国内外学者对叶片的振动已经做了很多研究.1997年,Carmakar等人[1]研究了复合材料旋转变截面板模型.考虑了预扭转角,利用有限元的方法研究了变厚度板各参数对其稳定性的影响.2000年,Lin等人[2]将叶片简化成含预扭转角的Euler-Bernoulli梁模型.利用哈密顿原理研究了含弹性约束的结构在简谐外激励作用下的动力学响应,通过计算分析了剪切变形、转动惯量、预扭转角等对结构振动频率的影响.2001年,Hong等人[3]将发动机叶片模拟为含预扭转角的板,将叶片材料简化为均匀、各向同性材料,采用瑞雷李兹法,忽略了剪切变形影响,得出了预扭转角和轮毂半径对板振动的影响规律.2002年,Banerjee等人[4]研究了变截面旋转梁的振动问题.指出了关于系统应变能和动能中的几个不准确的地方,并指出在能量表达式中忽略某些重要项注定会降低有限元的分析精度,从而导致数值分析结果的重大误差,同时也指出对于矩形截面叶片的研究可拓展到变截面,从而接近工程实际叶片.2004年,Kee等人[5]将叶片简化成含预扭转角的复合材料旋转壳模型.考虑了预安装角、横向剪切变形和转动惯量,研究了各个参数对振动的影响,并与实验数据进行对比.2006年,Sabuncu和Evran等人[6]将叶片简化成旋转的含预扭转角的变截面翼型梁模型.通过Euler- Bernoulli梁理论和有限元的方法研究了不同参数对叶片振动的影响.2008年,Lin等人[7]将叶片简化成含预扭转角变截面梁模型,利用Euler-Bernoulli梁理论建立了动力学方程并进行数值模拟.Lim 等人[8]研究了轮盘耦合的发动机叶片.将叶片简化为厚度线性变化的变截面梁模型,研究了各个参数对整体振动的影响.2011年,张伟等人[9]研究了航空发动机叶片的非线性振动问题,将叶片简化为功能梯度材料薄壁悬臂梁,考虑几何大变形的影响,利用Hamilton原理推导了非线性动力学方程,通过数值模拟研究了其非线性动力学行为.2013年,李克安等人[10]将叶片简化成变截面悬臂梁模型.根据叶片的受力分析,通过引入叶片的变形系数,建立了叶片的自由振动方程.然后利用Ritz-Galerkin方法得到了一种可以计算叶片静频和动频的数值方法,计算结果与实验测量结果比较接近.2015年,马艳龙等人[11]研究了端部附有集中质量的变截面梁的横向振动特性.基于假设模态法给出了其固有频率及振型函数的计算方法,并通过工程实例验证了该方法的有效性.2016年,姜萌等人[12]介绍了叶片组模型的等效建模方法,以固有振动特性相近为等效准则,将有限元模型中周向环绕的叶片组等效为变参数圆柱型正交各向异性环形板,并通过理论推导和计算得到了环板模型的几何与材料等物理参数.

国内外学者对发动机叶片进行了大量研究.对于叶片模型的选择各有不同,多数研究者采用了梁模型,部分人采用了板模型和壳模型.对于变截面模型,大多学者采用变截面翼型梁模型和变截面盒型梁模型,部分学者研究了楔形梁模型,而以变截面板模型建模的较少.对于叶片的研究,采用数值仿真方法的较多,而求解精确解的较少.本文主要将叶片简化成变截面板模型,考虑其预扭转角和预安装角,研究了叶片在受气动力与离心力作用下的非线性动力学行为.

1 变截面旋转叶片模型

将变截面旋转叶片简化为固定在轮毂上的变截面板,如图1所示.

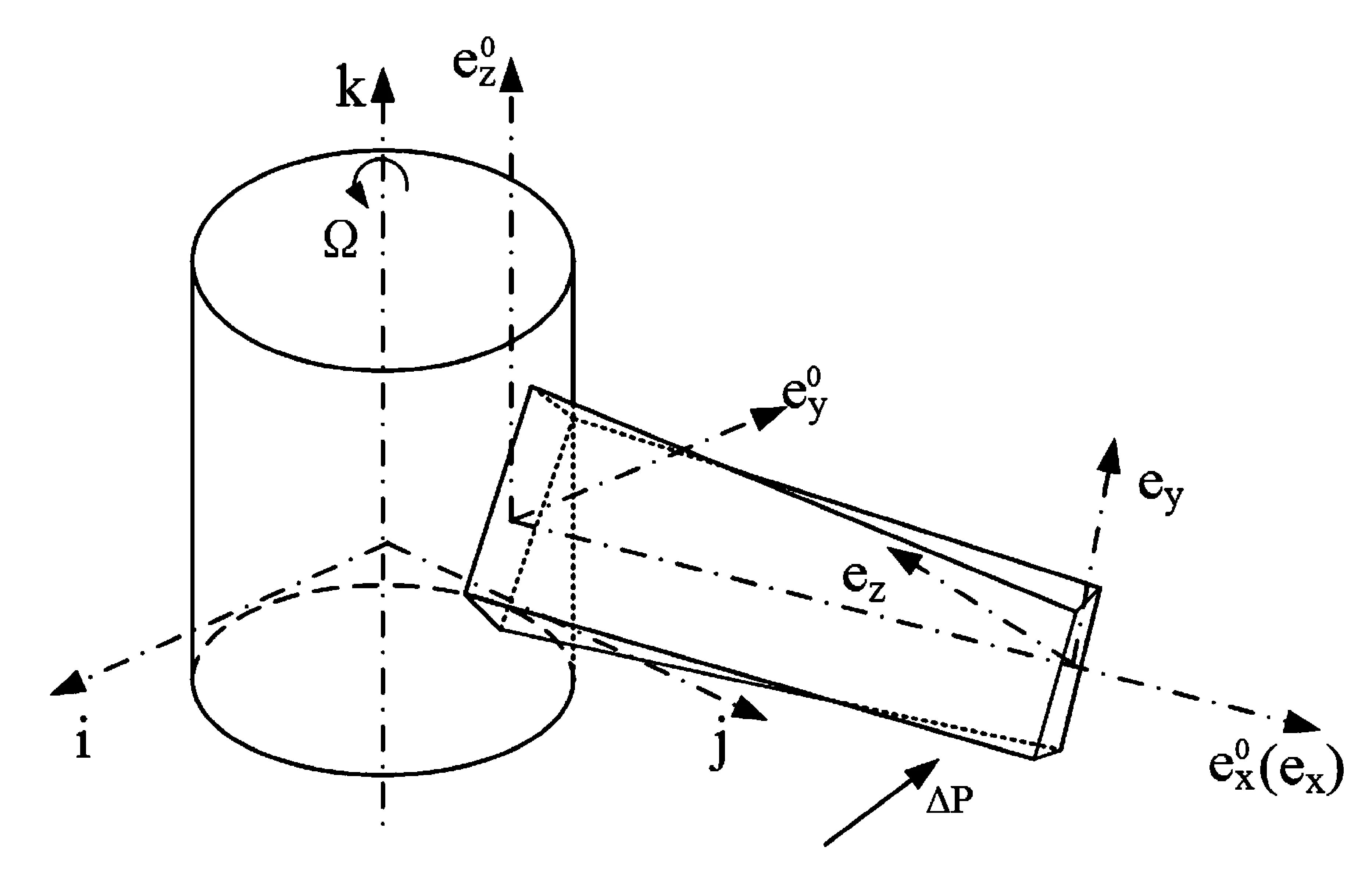
图1 变截面叶片模型Fig.1 Model of blade with varying cross-sections

根据各个坐标系的关系,给出如下旋转坐标系与惯性坐标系、截面坐标系与旋转坐标系之间的关系：

(1a)

(1b)

利用三阶剪切理论表达位移场：

u(x,y,z,t)=u0(x,y,t)+zφx(x,y,t)-

(2a)

v(x,y,z,t)=v0(x,y,t)+zφy(x,y,t)-

(2b)

w(x,y,z,t)=w0(x,y,t)

(2c)

其中,u0、v0、w0表示截面坐标系下任意一点在x、y、z方向上的位移.根据Von Karman大变形理论,应变-位移关系可表达为：

(3a)

(3b)

其中：

(4a)

(4b)

(4c)

(4d)

材料为各向同性材料,其本构方程为：

(5)

其中：

(6)

其中,E为材料的杨氏模量,ν是泊松比,ks为剪切修正系数.

将截面坐标系下的点转到惯性坐标系下,用坐标表示出叶片上每一点的位置函数有：

R(x,y,z,t)=[(R0+x+u)cosΩt-

(y+v)sinΩtsinθ+(z+w)sinΩtsinθ]i+

[(R0+x+u)sinΩt-(y+v)cosΩtcosθ-

(z+w)cosΩtsinθ]j+

[(y+v)sinθ+(z+w)cosθ]k

(7)

因此,动能的表达式为：

(R0+x+u)2Ω2+

(8)

叶片沿着展向的离心力为：

(9a)

沿着弦向的离心力为：

(9b)

势能包括应变势能和离心力做功产生的势能,其表达式分别为：

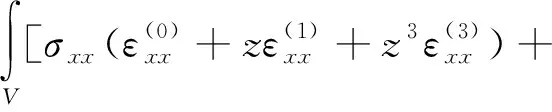
(10a)

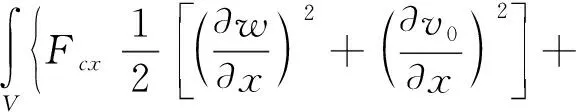
(10b)

式中U1为变形产生的势能,U2为离心力做功产生的势能.

外力做功由气动力产生,气动力只考虑垂直于叶片表面的力.气动力的表达用一阶活塞理论表示：

(11)

故气动力做功有如下表达：

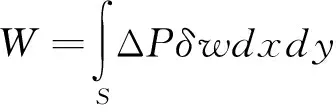
(12)

利用哈密顿原理建立方程,将方程(8)、(10)、(12)代入哈密顿方程中,展开得到了以下5个广义位移表示的方程：

(13a)

(13b)

(13c)

(13d)

(13e)

2 Galerkin离散

对所得方程进行无量纲化,其无量纲变化表达式为：

(14)

对无量纲后的方程进行Garlerkin离散,离散函数采用如下表达式：

(15a)

(15b)

w0=w1(t)X1(x)Y1(y)+w2(t)X2(x)Y1(y)

(15c)

(15d)

(15e)

其中有：

Xi(x)=sinλix-sinhλix+αi(coshλix-cosλix)

(16a)

Y1(y)=1

(16b)

(16c)

cosλiacoshλia+1=0

(16d)

cosμjbcoshμjb-1=0

(16e)

(16f)

由于所建模型的横向振动比其他两个方向的振动要大很多,将截断后的u、v、Φx、Φy方向的方程带入w方向,并将系数进行化简,整理得到两自由度非线性动力学方程如下：

a7w12+a8w22+a9w1w22+a10w12w2+

(a11+a12k)w1w2+(a13+a14k)w12+

(a15+a16k)w22+(a17+a18fcosΩ1t+a19k)w1+

(a20+a21fcosΩ1t+a22k)w2=a23fcosΩ1t

(17a)

(b11+b12k)w1w2+(b13+b14k)w12+

(b20+b21fcosΩ1t+b22k)w2=b23fcosΩ1t

(17b)

式中,q为气动力系数,k为截面斜率系数,f为扰动转速系数.

3 摄动分析

本文主要考虑1∶ 3内共振关系和1∶ 2亚谐共振情况.采用渐近摄动法进行分析,引入小参数ε,

(18)

式中Ω1、Ω2为不同的两个线性频率,σ1、σ2为两个不同的调谐参数.

运用渐近摄动法得到直角坐标系下的平均坐标方程为：

dx1=-(σ1+b11+b12k+b14kf+b13f)x1-

2(b23+b24k+b25k2)x1x2x4

(19a)

dx2=-(σ1+b11+b12k+b14kf+b13f)x1-

2(b23+b24k+b25k2)x1x2x4

(19b)

dx3=(σ2+b27+b28k+b29kf+b30f)x4-

(19c)

dx4=-(σ2+b27+b28k+b29kf+b30f)x3-

(19d)

4 数值模拟

基于上述得到的平均方程,利用Runge-Kutta法进行数值模拟,研究随着扰动转速系数f变化时,旋转叶片的非线性动力学行为.选定初始参数为：

σ1=3.68,σ2=0.47,q=0.8,k=0.85,

b11=-4.7124,b12=-0.6,b13=-0.44,

b14=-0.84,b15=0.0012,b16=-0.0015,

b17=4.265,b18=6,b19=10,b20=-2,b21=8,

b22=-7.65,b23=9.665,b24=-28,b25=6,

b26=4,b27=-0.18,b28=-0.8,b29=-1.6,

b30=-6.274,b31=-0.0012,b32=0.0015,

b33=-24.5,b34=2.2,b35=3.4,b36=2.4,

b37=0.6,b38=-1.225,b39=-0.176,

b40=1.6,b41=2.8 .

改变方程中扰动转速系数f,研究扰动转速对系统振动响应的影响.当扰动转速系数f从0变化到10的过程中,发现系统出现了混沌概周期、概周期和多倍周期现象,其波形图、相图、频谱图如图2、图3与图4所示.当f为0.855,系统出现混沌现象；当f为3.558时,系统为概周期现象；当f为6时,系统为多倍周期现象.

图2 f=0.855时系统的混沌运动Fig.2 Chaotic motion of system when f=0.855

图3 f=3.558时系统的概周期现象Fig.3 Quasi-periodic motions of system when f=3.558

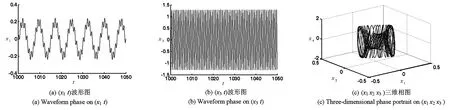
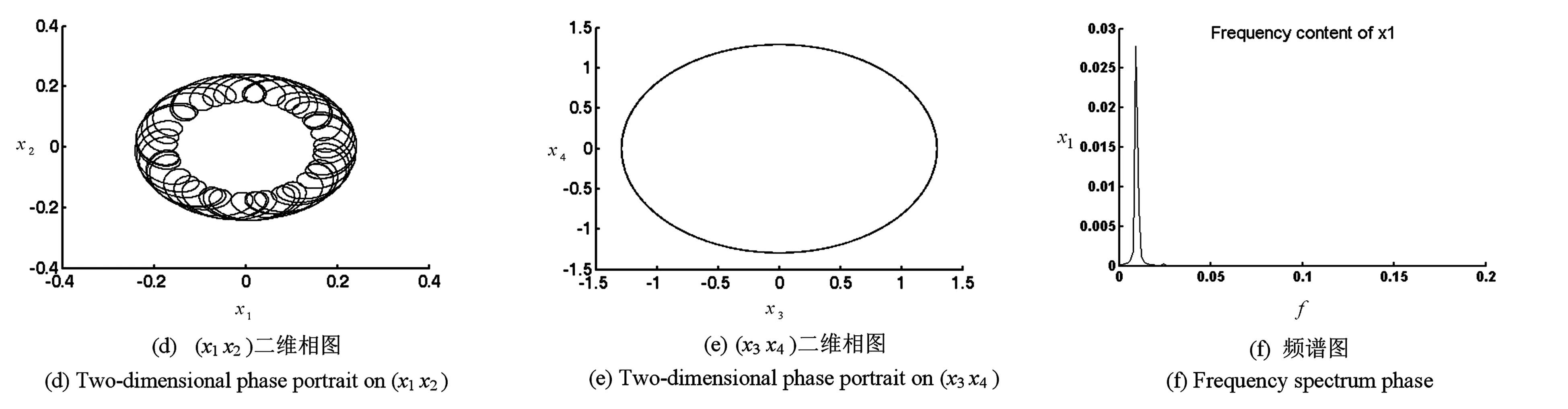
图4 f=6时系统的倍周期运动Fig.4 Periodic motions of system when f=6

5 结论

将叶片简化成变截面旋转叶片模型,利用Hamilton原理建立了叶片的非线性偏微分运动控制方程.利用Galerkin方法对所得方程进行离散,得到了常微分形式的运动控制方程.在系统1∶ 3内共振情况下,利用摄动分析得到了四维直角坐标系下的平均方程,并用数值方法研究了扰动转速对系统的非线性动力学行为的影响.结果表明,扰动转速对系统动力学特性有重要影响,扰动转速变化时,系统出现了混沌、概周期和多倍周期现象等多种复杂动力学行为.