基于样条曲线描述的超声速喷管型面优化设计

吴盛豪, 廖达雄, 陈吉明, 陈钦, 裴海涛

(中国空气动力研究与发展中心 设备设计与测试技术研究所, 四川 绵阳 621000)

超声速喷管的目的是保证超声速风洞试验段获得设计马赫数，并使试验段马赫数分布均匀、保持平直气流。在传统二维喷管设计方法中，一般基于特征线原理设计喷管位流型线[1]，在一定的边界层假设条件下，对喷管的位流型面进行边界层修正[2]，得到喷管型面曲线。随着计算流体力学和计算机技术的快速发展，分析设计的方法(design by analysis)被引入到喷管设计中[3-4]，广泛应用于火箭发动机喷管和高超声速飞行器尾喷管优化设计[5-6]，并取得良好的应用效果。超声速风洞喷管与火箭发动机和超声速飞行器尾喷管设计存在一定相似性，但对流场品质要求更高，拟将基于CFD的搜索算法应用到超声速风洞喷管设计中，以期获得更优的试验段流场品质。在实际应用喷管型面优化设计时，面临2个重要问题：喷管型面的参数化和优化目标的选取。喷管型面参数化的方法较多，高超声速飞行器的尾喷管可采用Akima三次曲线作为参数化的方法[5]，将燃烧室出口高度及喷管下板长度和偏转角作为设计变量，火箭发动机喷管可采用2段三次样条曲线进行构造[7],由于本文研究的超声速喷管对流场分布的均匀性要求较高，因此对型面的要求也更为精细，拟采用多段Spline样条曲线对喷管进行参数化；优化目标的选取直接关系到优化设计结果的质量，考虑到多段样条曲线参数化的喷管，流场品质不确定度较高，拟选择试验段轴向马赫数与设计值的均方根误差作为优化目标，即可保证喷管达到设计马赫数的同时具有较优的流场分布。

1 优化问题的描述

1.1 优化设计对象

本文研究对象是中国空气动力研究与发展中心的0.6 m连续式跨超声速风洞的二维半柔壁型式低超声速喷管(见图1)。

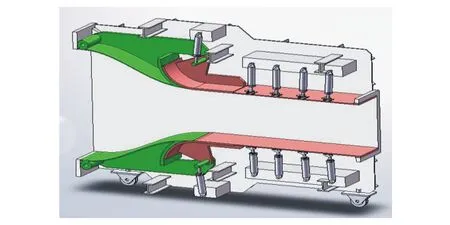
图1 0.6 m连续式风洞喷管结构示意图

风洞喷管膨胀段位流型面采用具有连续曲率的喷管型面设计方法——Sivells方法得到,利用经验估算的方法进行边界层修正[2]，即近似认为喷管超声速段型面上的边界层顺气流方向线性增长。该风洞在低超声速运行过程中，采用可调柔性板模拟喷管型面，试验段为四壁实壁，为消除气流流动过程中沿壁面边界层逐渐增厚对试验段流场品质的影响，试验段的上下壁板扩开角可在(-0.5°,1°)范围内实现连续调节。

1.2 优化问题的定义

风洞流场校测试验中，利用(1)式计算风洞模型区内沿轴向马赫数与均值的标准差(σM)作为表征流场均匀性的指标,据此本文选择(2)式计算得出的试验段实际轴向马赫数与设计值的均方根误差(ReM)作为优化目标。

(1)

(2)

式中,Mi为试验段内轴向测点马赫数,Mdesign为喷管设计马赫数,本文选择M1.5为设计对象。据此可提出如下优化设计问题:

优化目标: minReM

设计变量:h={h0,h1,h2…hn,θ}T

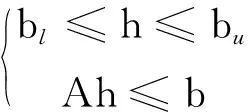
式中,h为设计变量,其中h0为喉道相对中心轴线高度,其后h1…hn为插值点高度;θ为喷管出口倾角亦为试验段壁板扩开角;bl,bu为设计变量的上下限,Ah≤b限定了分变量h1～hn按照递增的顺序排列。

优化问题中模型区内ReM直接反映流场波动情况,当ReM→0可判定模型区内斜激波或膨胀波基本被消除,流场均匀性达到要求;同时由于ReM是试验段实际马赫数与设计的误差,所以当其趋于0时,可判定试验段马赫数达到设计值。

1.3 CFD计算验证

优化设计过程中涉及到对候选喷管型面进行气动性能评估,选择CFD的方法进行评估。对风洞高速段建立计算模型,计算域包含收缩段、喷管段和试验段,利用对称条件建立四分之一模型。喷管选择M1.5型面喷管静调值,试验段壁板扩开角设为风洞调试过程中选择的0.1°,流动条件为风洞常规运行工况:总压100 kPa,常温,干燥空气介质。选择kw-sst湍流模型求解,给定高速段进出口压力作为边界条件,入口湍流度按试验测量值0.4%给定。

在0.6 m连续式风洞中,M1.5低超声速运行时,利用单点总压探头(如图2所示)移测的方式对试验段第一菱形区和模型区内轴向马赫数分布进行测量。其中单点总压探头直接测得波后总压,再利用(3)式通过迭代求解出测点马赫数。

图2 核心流波后单点总压探头

(3)

图3给出沿试验段中心轴向马赫数分布的试验和数值模拟结果,由于喷管出口和试验段入口存在折角,造成模型区内马赫数轴向分布出现剧烈波动,试验得到模型区(距试验段入口1 000～1 600 mm范围)流场指标:马赫数标准偏差σM=0.017;轴向马赫数梯度dM/dx=0.060。数值计算得到模型区内流场指标:马赫数标准偏差σM=0.012;轴向马赫数梯度dM/dx=0.049。

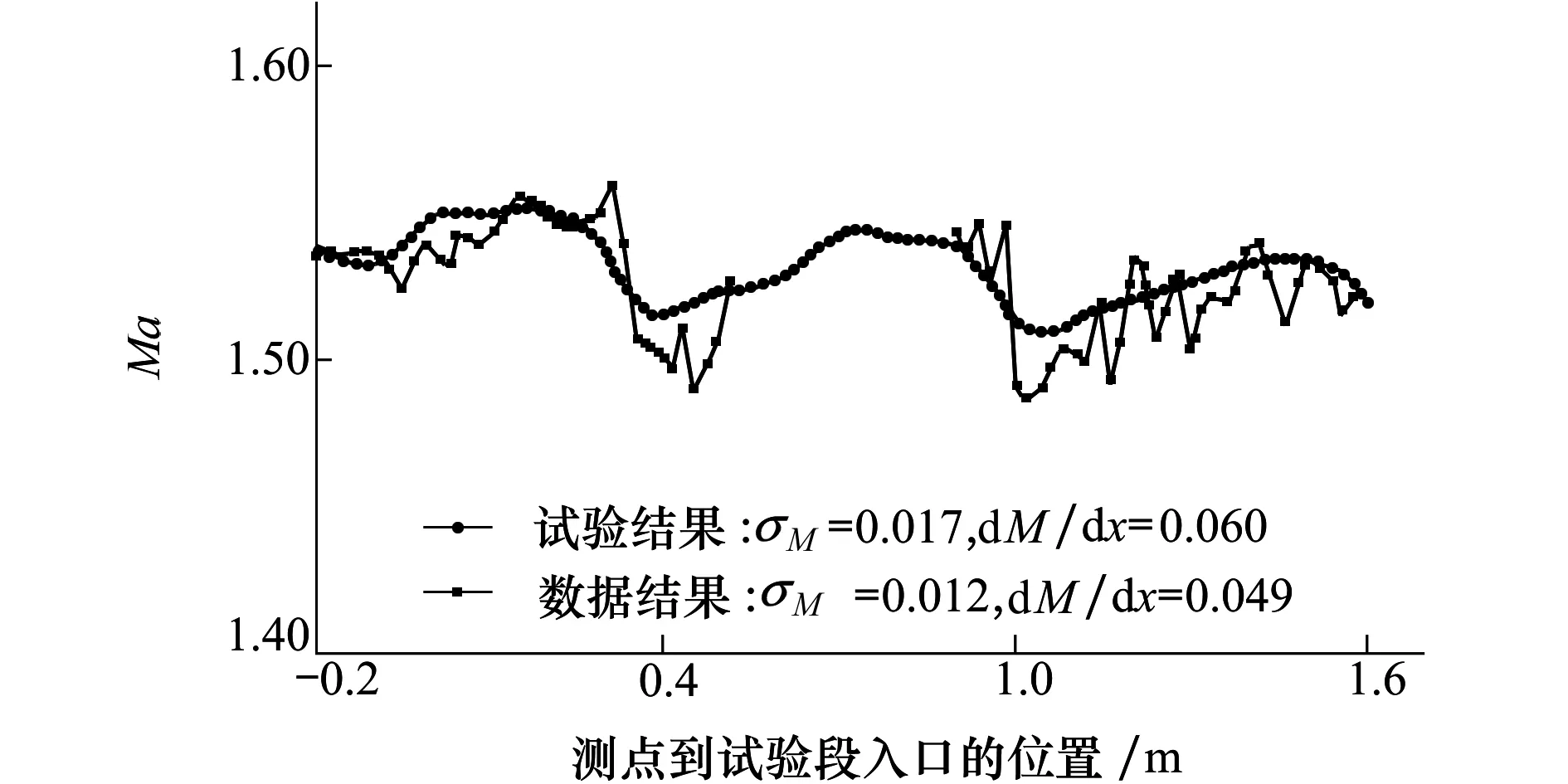
图3 试验段轴向马赫数分布

对比数值模拟结果和试验结果,试验段沿轴向马赫数分布规律吻合较好,σM和dM/dx指标计算误差在允许范围内。同时图4给出该状态下,CFD计算得到的试验段纵切面上密度梯度云图,从图中可以看出由于喷管出口和试验段壁板倾角不同,在连接处出现一道弱斜激波,经过壁板反射之后,造成试验段内的马赫数波动,与试验结果相同。

图4 试验段纵切面密度梯度云图(入口坐标:0)

上述CFD仿真计算可获得较为精确的试验段马赫数分布,对激波和膨胀波的捕捉也较为可靠,因此可将该CFD计算方法用于对候选喷管型面的气动性能评估。

2 喷管型面曲线参数化

2.1 喷管型面构造

喉道前的收缩段曲线通过(4)式描述的双三次曲线给出,式中:xm为两曲线前后连接点;D2收缩段出口截面半径,亦为喉道高度;D1收缩段进口截面半径;D轴向距离为x处的截面半径。

(4)

对于喉道后的扩张段,挠性喷管利用挠性板的弹性曲线模拟理论气动型面,其曲率变化一定是连续的,因此选择具有二阶连续导数的三次Spline样条曲线拟合喷管气动型面可保证气动型面具有连续曲率。如图5所示，P0,P1,…,Pn,Pout为插值节点,P0喉道位置,Pout为喷管出口位置。

图5 喷管型面曲线构造过程示意图

为求解三次样条插值函数的系数矩阵,给出端点处的第一边界条件即一阶导数,喉道处型面倾角为0,喷管出口处型面倾角取为壁板扩开角θ,据此可给出(5)式所示的第一边界条件。

(5)

2.2 插值点的选择

所选插值点应能够精确拟合喷管型面,而增加插值点数目导致设计变量增多,影响求解的效率,因此需对所选插值点的个数和位置进行研究,以找出最佳方案。

以0.6 m连续式跨超声速风洞原M1.5喷管设计型面为参照对象,将拟合型面与原设计型面曲线最大高度差δmax作为评估,找出最佳插值点数目和分布方案,使得δmax≤0.05 mm(喷管型面静调误差)。

利用喷管出口高度和扩张段长度分别对型面纵坐标和横坐标做无量纲处理,利用搜索算法以minδmax为目标,搜寻不同型面控制点数目(3～8)下的,最优控制点分布方案。从表1中数据看出,随着控制点数目的增加,拟合型面与原型面误差逐渐降低,当控制点数目为6时,按照搜寻到的最佳节点分布方案,拟合误差为0.01 mm，达到0.05 mm的误差要求。

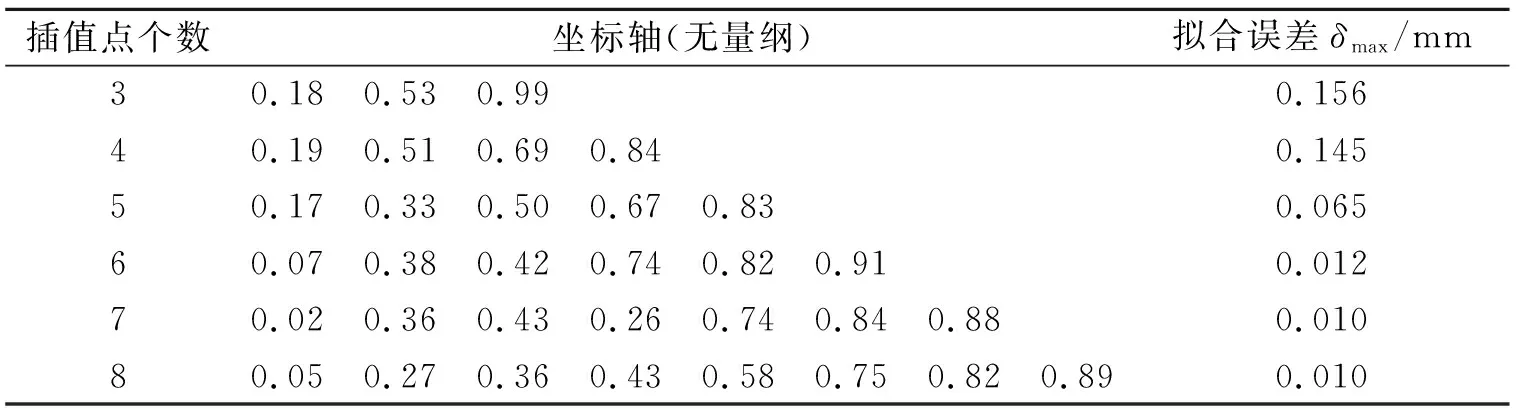
表1 不同分布插值点的型线拟合误差

3 基于高斯过程模型的重启优化算法

在应用优化算法进行喷管型面设计时,面临2个问题:优化算法的全局特性和气动性能CFD计算的效率问题:为提高全局特性,本文构造梯度优化算法的重启机制;同时利用高斯过程模型构建设计变量与气动性能指标之间的关系,以减少CFD评估次数。

3.1 重启搜索算法

基于梯度的最优化算法具有求解次数少、收敛速度快的优点。但是这类方法都属于局部最优化方法,能否收敛到全局最优点,取决于搜索的起始点。为提高梯度搜索的全局特性,借用NSGA算法中提出的拥挤距离概念,构建梯度算法的重启机制[8]。可在由某初始点x0执行梯度搜索到达局部最优点之后,重新产生新的起始点xrs搜索。为了提高算法的效率,则需要使xrs位于没有探索过的区域。这个条件可以用最大化拥挤距离来定义。假设已评估的设计点集合X⊂D,新的设计点x∈D,定义拥挤距离为如下的函数:

(6)

3.2 高斯过程模型介绍

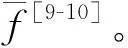
(7)

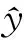
3.3 算法框架优化准则

基于高斯过程替代模型的优化算法框架如图6所示。

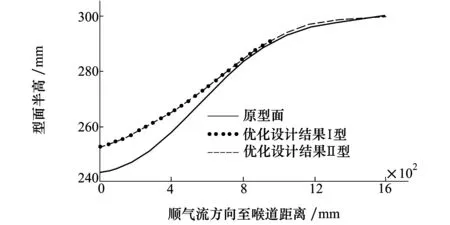
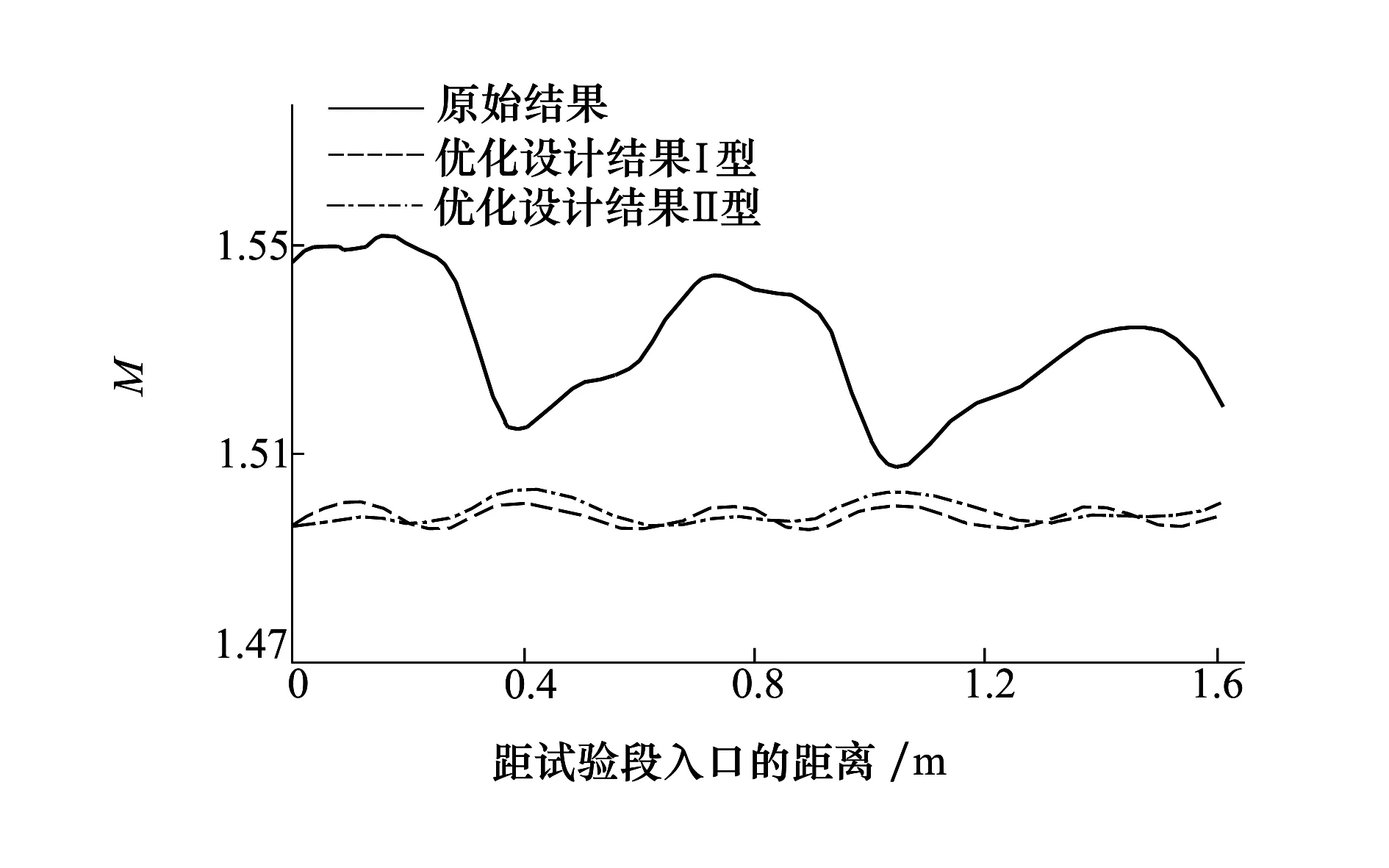
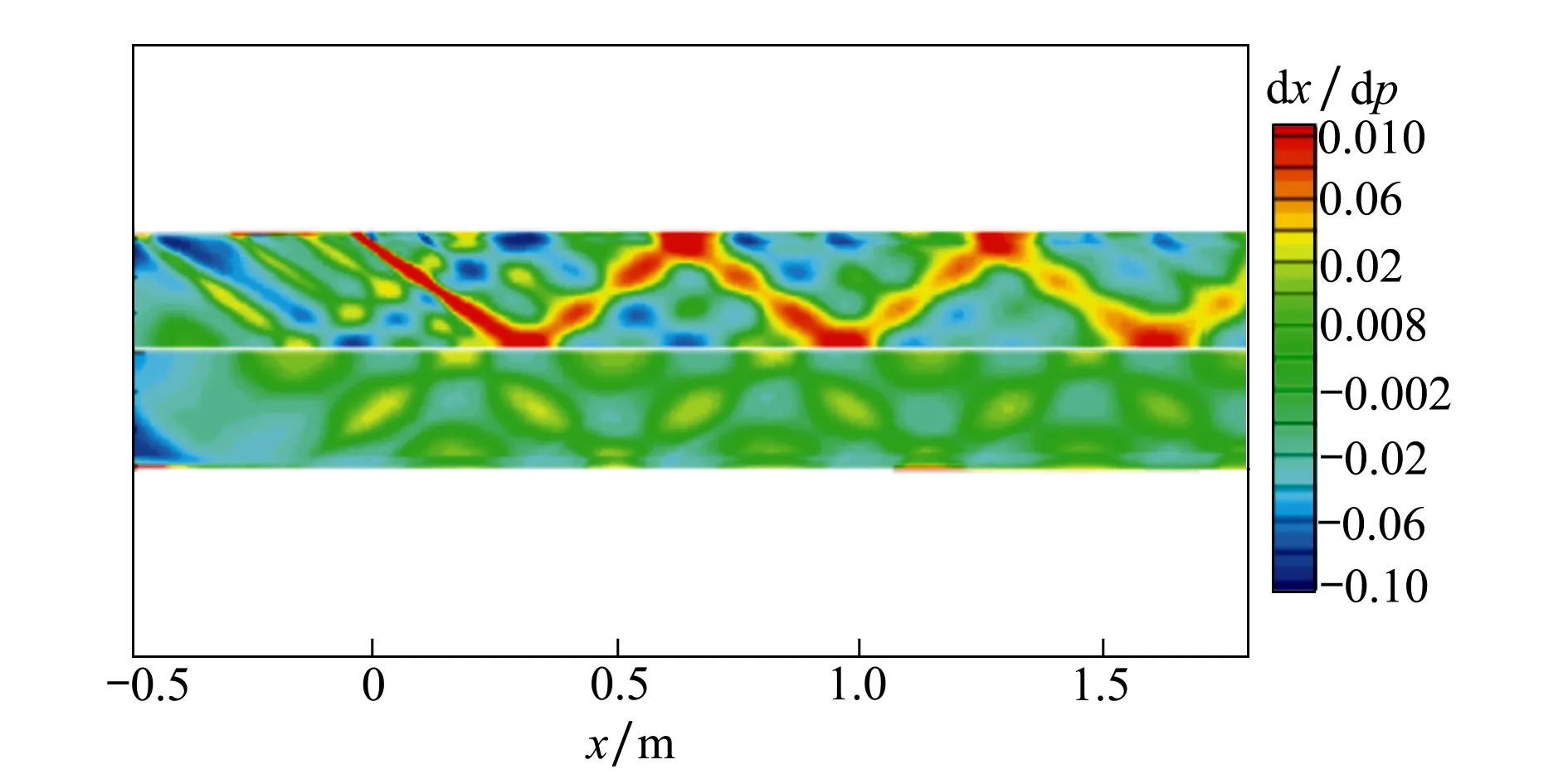
1.procedure NOZZLE OPTIMIZATION(lb,ub)2. Input:nmax,Ω3. D←[bl,bu]4. neval←05. D←ϕ6. K←ϕ7. n←dim(D)8. n0←11n-19. d0←{d10,…,dn00}⊂D10. Evaluation:κ←{κ(d0,Ω)}11. neval←neval+n012. D←D∪d0,K←K∪κ13. Modelling:Φ:DK←DK14. while(neval

图6 基于替代模型的优化算法框架

D为设计空间(设为n维),Ω为流动条件,κ为所选的气动性能参数。首先从设计空间中利用拉丁超空间试验设计方法(Latin hyperspace design, LHS)选择11n-1个初始采样点,并评估其气动性能。根据已评估的设计点参数和气动性能建立高斯过程模型;利用高斯过程替代模型来探索设计空间,选择需要评估的候选设计点;评估候选设计点的气动性能。然后重复建模-选择候选点-评估候选点的过程,直到得到满意的设计结果或者优化资源消耗完毕。在这个算法中,实际的气动性能评估计算只发生在图6中的第10步和16步,优化过程则基于替代模型完成(第15步)。

3.4 算法性能验证

针对经典2维算例,限定计算目标函数的值100次,考察算法的性能,其优化结果如表2所示。在这6个函数中,Sphere和Ellipsoid是单模态函数,其余均为多模态函数。函数最小值都为0。从表2中可以看到,除模态数量极为庞大的Griewank函数和Rastrigin函数之外,均可以得到1×10-4量级的优化结果。

表2 基于高斯过程模型的重启优化算法性能

4 喷管优化设计结果

针对0.6 m连续式跨声速风洞,M1.5型面、运行总压100 kPa的工况,对1.2节中描述的优化问题开展单目标优化。优化设计过程中允许的总气动评估次数为1 000次,梯度算法最大迭代次数2 000,重启点个数89,初始采样点个数81,同时CFD进行气动评估的过程中利用前次结果为后次计算赋初值,以加快收敛。气动评估次数达到600次后,分别在第534次和第561次得到较优的2个设计结果,考虑到设计变量多达8个,因此求解效率相对较高。

表3给出了优化设计结果,结合图7给出的喷管扩张段型面曲线,可以看出,2个优化设计结果型面曲线差别较小,同时流场品质指标也较为接近。

与原设计型面对比,优化设计型面喉道高度由243.55 mm变为252.9 mm有效解决了原喷管型面马赫数偏高的问题,提高了喷管设计型面马赫数的精准度。

图7 喷管扩张段型面曲线对比

图8 试验段轴向马赫数分布

优化设计结果计算步数变量设计结果/mmh0h1h2h3h4h5h6θ流场品质σMdM/dxorigin243.55246.43271.61275.83294.00297.45298.740.100.0120.049 result 1534252.98256.70274.53277.99297.19298.63299.630.110.001 30.001 result 2561252.93256.41274.65278.03297.12298.66299.620.120.001 90.003

图8给出优化设计得到的试验段轴向马赫数分布,结合表3的流场指标,可以看出优化设计得到的试验段内马赫数分布均匀性较好,流场均方根偏差由0.012降低到0.001～0.002左右,试验段模型区内轴向马赫数梯度在0.001～0.003范围内,满足设计指标的要求。由于本将试验段与喷管进行一体化设计,即设计变量之一的喷管出口角度θ和试验段壁板扩开角相等,改善了喷管出口和试验段入口曲率不连续的问题,试验段内的弱压缩波和弱膨胀波较原型面减弱明显,从图9优化设计前后密度梯度分布云图亦可看出。

图9 优化前后试验段密度梯度分布云图

5 结 论

基于本文提出的喷管优化设计框架可有效地获得流场品质较高的超声速喷管型面:选择具有二阶连续导数的三次spline样条曲线和最优插值点分布方案可较为精确地描述喷管型面;将试验段实际轴向马赫数与设计值的均方根误差(ReM)作为优化目标,可在确保设计马赫数准确度的同时保证试验段流场品质;基于高斯过程模型的重启优化算法,改善了优化问题全局特性的同时较大地提高了求解效率。

基于本文提出的优化框架,均方根偏差降低到0.001,仍有提升的空间,下一步可考虑将算法框架扩展到包含多目标优化、多设计变量如喷管长度、最大膨胀角等参数,以进一步提升喷管性能。