模糊需求下农超对接合作博弈收益策略研究
2018-09-07曲冲冲何明珂
曲冲冲, 何明珂, 熊 英
(1.北京工商大学商学院,北京 100048; 2.北京物资学院物流学院,北京 101149)
农产品进城一直是“三农”问题的重中之重,我国商务部、农业部发布了《关于开展农超对接试点工作的通知》,拉开了“农超对接”试点工作的序幕。“农超对接”是农户将生产出来的农产品交付给农业合作社,由农业合作社销售给城市的连锁超市,农业合作社再将销售收入支付给农户的模式。这种模式可以减轻农户作为个体单独售卖产品的困难,合作社将分散的农户的产品统一收购起来,与连锁超市谈判销售条件,可以保证农产品的销售价格和农民的相关权益,连锁超市直接面对农业合作社,也可获得规模效益,这是一个农户、合作社和超市三方获益的模式,目前在我国农产品销售过程中普遍采用。
但是“农超对接”模式的应用涉及到2个关键问题:(1)超市要根据市场对农产品的需求量进行采购,而市场需求量是不确定的,其采购源头的农户生产量是一定的,在需求不确定的情况下,农户、合作社和超市对采购量-销售量的确定十分困难,这直接影响到三方合作的方方面面;(2)在超市销售量(即市场需求量)不确定的情况下,如何确定农产品的销售价格,即农户向合作社的销售价格及合作社向超市的销售价格,也是三方合作能否持续的关键,自然也是决定“农超对接”模式是否可持续的关键。这涉及到对“农超对接”的认识及三方收益分配博弈问题。本研究旨在研究在面对模糊需求情况下三方合作时的收益分配博弈问题。
在对“农超对接”模式的认识上,刘晓峰提出,“农超对接”是农产品流通的重要形式之一,可以有效地降低农产品在物流过程中产生的相关费用[1]。李莹等认为,“农超对接”实现了生产与销售的直接链接,是农业生产力发展趋势的重大变革[2]。施晟等认为,“农超对接”是超市直接从生产端采购农产品或者农业生产者直接向零售商供应农产品的一种流通交易模式[3]。赵佳佳等认为,提升参与者之间的合作能力以及合作意向能够提高“农超对接”模式的组织效率[4]。郑鹏等认为,“农超对接”模式中超市是农户与市场的纽带,可以有效地发挥流通带动生产的作用[5]。解东川通过应用集体行动理论与社会嵌入理论,对中国传统农村社区持续分化导致的多元化农村社区类型进行了分类,进而通过演化博弈的双种群理论探讨合作社与农户合作行为的演化规律[6]。Michelson等在研究尼加拉瓜地区农户与超市合作模式中,对比了农产品在传统市场与超市的销售价格,同时指出农户在与超市合作的过程中,为了应对价格变化会支付更多的合同保险[7]。刘兵等认为,从超市、生产者以及政策3个方面对“农超对接”模式的发展有着积极的促进作用,并且有利于提升农产品标准化水平[8]。李政认为,“农超对接”模式的应用对农产品安全供给提供了有益的启示[9]。
在“农超对接”模式合作收益分配问题上,王志刚等在对调查数据的研究分析基础上运用Shapley值法对现有收益进行分配[10]。史文倩在研究“农超对接”主体收益分配分析中,运用实例计算出合作博弈基础上各参与单位的利益收入,运用带有风险修正因子的Shapley值法进行三方利益结构的调整,使得合作方案更加趋近合理[11]。Hu等对2种不同供应链组成模式的各方合作方式与利益分配进行了比较研究,通过一个包含风险趋避的零售商、风险中性的制造商和分销商的三级供应链与包含风险趋避的零售商和风险中性的分销商的二级供应链之间的对比,指出两者的区别,并发现与风险中立的零售商相比,风险趋避的零售商在相同的情况下获取的利润更少[12]。Arani等在介绍协调零售商-制造商关系时提出了混合的分享期权合约,通过将欧式看涨期权机制和收益分享机制结合,消除了传统经典合同的缺点,通过博弈方法对几种不同情况进行检验,获得在实现纳什均衡条件下零售商和制造商的订货数量[13]。
关于模糊需求,学者们进行了不少探索。Liu在研究企业追求利润最大化问题的基础上,通过运用模糊系数来表示模拟情况下的确定性程度,通过设计1个两级数学规划对利润的上下界进行约束;运用对偶定理与分离变量法将两级数学规划转换成为1个典型的一级数学规划进行处理[14]。付秋芳等在现有Shapley值法的基础上充分考虑了包括风险控制、技术创新、努力程度以及资产投入4项修正因子,并且运用灰色关联度系数确定修正因子的权重,克服了修正系数的主观性与随意性的弱点[15]。刘磊等通过对“农超对接”模式发展过程中的非合作博弈与合作博弈的对比,以及对市场需求函数中α与β关键参数的灵敏度分析,结合实际算例证明得出,合作博弈能够提高供应链总利润[16]。张瑜等通过运用Shapley值法对农户、合作社与超市联盟博弈利益分配机制进行了研究,从理论上解释了合作社与超市相互合作关系的稳固性[17]。陈红华等在对可追溯系统利益分配研究的基础上,通过带有风险修正因子的Shapley值法对可追溯系统各个环节的利益分配情况进行了测算[18]。
通过文献发现,关于“农超对接”模式、利益分配机制等方面已有很多相关研究,但尚无考虑模糊需求对于“农超对接”三方合作机制的影响方面的研究。在现实生活中,消费者从超市采购农产品的数量是不稳定的,超市从合作社或农户采购的农产品数量也带有很大的不确定性,下游不确定的需求很难用确定的数值与概率去描述,但可以利用模糊集理论来描述市场需求的不稳定性以及市场需求函数中相关参数的不确定性。基于以上构思,本研究利用模糊需求理论,将需求函数中的参数视为三角模糊变量,建立农户、合作社、超市三级供应链4种合作模式的模糊需求博弈模型,通过Shapley值法计算三级供应链各方收益,并得出“农超对接”最佳合作模式。
1 评估模型及指标体系
考虑我国“农超对接”的一般情形,农户作为农产品生产者,将农产品出售给合作社;合作社作为农户的合作组织,负责将农户的农产品进行统一收购,并统一销售给超市;超市作为专业销售渠道,从合作社采购农产品后通过销售门店售出。
由于农产品市场需求量是不断变化的,所以在建立模型时引入了模糊集理论辅助模型的建立。关于模糊集,有如下定义:
为了将问题描述得更加清楚而不失代表性,假定市场需求以超市的销售量代表,记为α,且超市向合作社采购的量、合作社向农户收购的量都是α,在上述“农超对接”的一般情形下,需求函数可以表示为:D(PS)=α-βPS,其中α为大于零的不确定常数,代表需求的不确定性;β表示超市销售价格PS对市场需求的敏感度,显然β的取值范围也是不确定的;在上述模型中,PS是决定农户、合作社和超市三方利益的关键,取值为当时当地的市场平均价格。
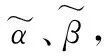
为了进一步研究的方便,设定以下变量与参数:
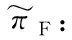
本研究进行了以下假设:
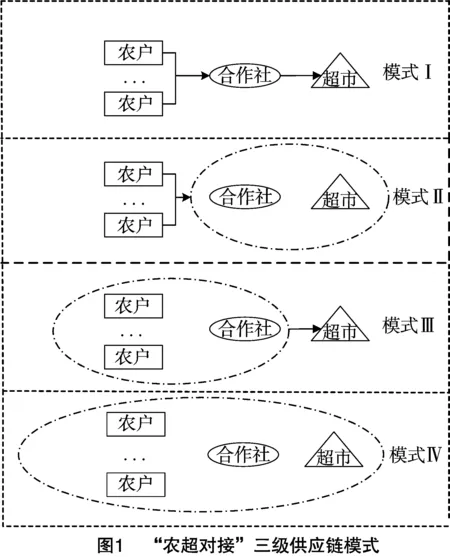
“农超对接”模式下的农户(F)、合作社(D)、超市(S)三方合作可有4种模式,如图1所示。
模式Ⅰ:F、D、S三者相互独立经营,决策过程互不干扰,记为(F,D,S)型;模式Ⅱ:D与S组成D-S联盟,而F与D-S联盟相互独立经营,且F占主导地位,记为(F,D-S)型;模式Ⅲ:F与D组成F-D联盟,而S与F-D联盟相互独立经营,F-D联盟占主导地位,记为(F-D,S)型;模式Ⅳ:F、D、S三者合作形成联盟,记为(F-D-S)型。
除图1所示的4种模式外,还有一种农户与超市合作形成联盟的模式,合作社此时不起作用,原先的三级供应链转化为二级供应链,这种情形暂不研究。
根据模糊集理论,市场模糊需求函数的λ水平集可表示为:

2 模型求解
基于上述模糊需求模型,可利用合作与非合作博弈方法对农户、合作社和超市的上述4种合作模式进行求解。
2.1 (F,D,S)型3层主从模型
在(F,D,S)型中,农户、合作社、超市三者各自独立经营,经过非合作博弈达成Stackelberg均衡,形成的三级供应链总收益模型为:
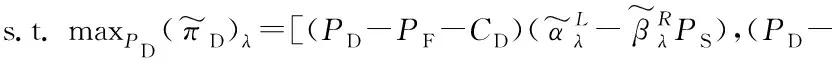
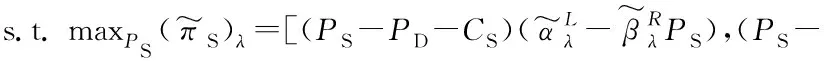
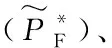
此时,农户、合作社、超市的模糊收益的λ水平集分别是:
后来,飘浮在小房里的空气越来越怪,易非已彻底被他们当做一个客人“供”起来了,他们都对她客气,格外地客气,格外地把她当外人。
为了简化公式,分别用A、B表示如下公式:
2.2 (F,D-S)型2层主从博弈模型
在(F,D-S)型中,合作社与超市组成两方合作联盟,农户与联盟遵循农户为主导的Stackelberg均衡,经过博弈后的供应链总收益模型是:
此时,农户与联盟的模糊收益λ水平集分别是:
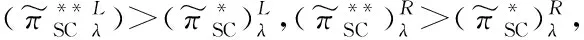
2.3 (F-D,S)型2层主从博弈模型
(F-D,S)型2层主从博弈模型中,农户与合作社形成两方合作联盟,联盟与超市遵循联盟占主导的Stackelberg均衡,经过博弈后的供应链总收益模型是:
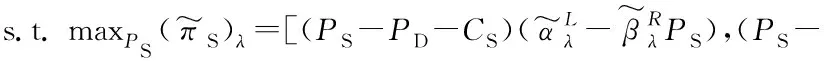
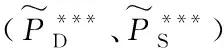
此时,联盟与超市的模糊收益λ水平集分别是:

可以看出,(F-D,S)型的模糊收益优于(F,D,S)型的模糊收益。
2.4 (F-D-S)型合作博弈模型
在(F-D-S)型中,农户、合作社、超市形成三方合作联盟即供应链,经过博弈后的供应链总收益模型为:
此时,三方合作联盟的模糊收益λ水平集为:
通过对以上4种供应链合作博弈关系的对比,得出4种模式的供应链总收益为:
可以看出,农户、合作社、超市形成的三方合作供应链模糊收益λ水平集明显优于其他3种模式,此时,供应链系统的模糊总收益达到最优,三者独立经营互相竞争时的供应链系统模糊总收益最差。
据此,需要激励农户、合作社、超市三方共同合作形成联盟,从而达到整体收益最大化。但是,三方是否能够合作,取决于总收益在三方之间如何分配,从三方之间任何一方的角度看,合作后的收益应不低于在其他合作博弈模式下取得的收益,否则这一“农超对接”模式无法实施。下面将研究这一收益分配问题。
3 用Shapley值法解决三方合作供应链模糊收益分配
在保证“农超对接”农户、合作社、超市形成供应链联盟三方总收益最大的同时,必须保证三方收益分配的公平合理,否则供应链联盟不可持续。为了解决这一问题,下面引入Shapley值法对三方合作供应链模糊收益进行分配。
Shapley值法是用于解决多方合作利益分配问题的一种数学方法,可以根据联盟成员的贡献大小来解决供应链联盟各成员间的收益分配问题。参与分配的各方的收益值一般表示为:
式中:Q是指集合I中包含成员i的所有子集,|q|为联盟Q参与合作博弈的个数,n为集合I中的元素个数,v(Q)是子集Q的收益,v(s/i)是从子集Q中减掉成员i后可获取的收益,v(Q)-v(s/i)指成员i对子集Q收益所作出的贡献。
为了公平分配三方合作联盟所获得的总体收益,下面采用模糊Shapley值法进行收益分配。根据前文运用模糊集方法得出的三方合作联盟收益为:
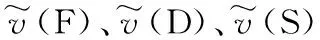
4 算例分析
为了进一步验证采用Sharply值法对供应链总收益进行分配的合理性,并计算出农户、合作社、超市形成三方合作供应链时各自的收入分配结果,下面引入算例。
有一个由若干家农户与一家合作社和一家超市组成的三级供应链联盟,该三方合作供应链联盟采取项目化运作方式,各方都进行资源投入,其他假设符合本研究前述假设要求。有关具体参数如下:
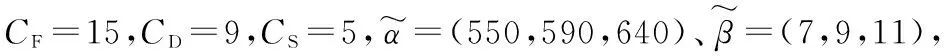
经过合作博弈后形成供应链联盟,供应链总收益模糊分配值在不同置信水平上的Shapley取值区间如表2所示。
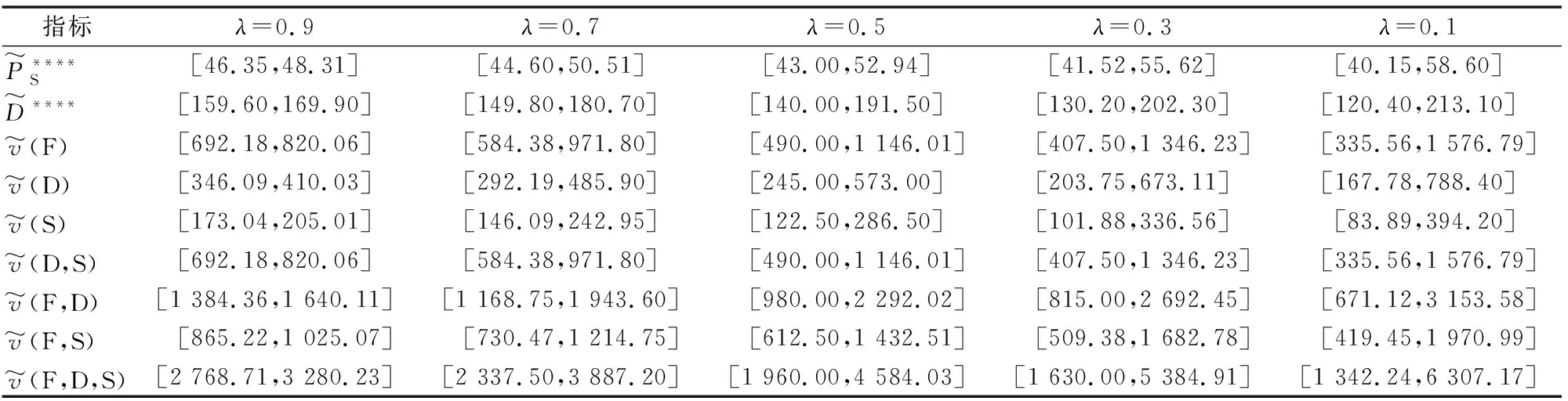
表1 三级供应链成员模糊收益及决策变量的λ水平集

表2 不同置信水平上各方的Shapley值的区间范围
农户、合作社、超市三方合作供应链联盟所分配的收益须要根据以上数据进行计算。三方合作联盟下销售价格P的基准值为:
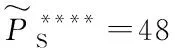
5 结论与总结
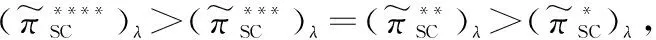
“农超对接”模式中农户、合作社、超市在形成三方合作供应链联盟时,总收益达到最大,为了保证合作的正常开展,收益分配策略是决定其合作关系存续的基础。因此,通过运用Shapley值法进行基于总模糊收益基础上的利益分配。运用算例对Shapley值法进行检验,并计算出农户、合作社、超市实现的各自收益,为三方合作的利益分配提供了理论依据;为改善城市农产品供应问题提供了基础性的解决方案,同时将进一步促进生鲜食品的可追溯性,为后续开展农超对接过程中出现的诸如食品安全等问题提供了基础性的指导。
