具混合时滞和不连续激励函数的Cohen-Grossberg神经网络周期解的存在性

张孟孟，赵前进

(安徽理工大学数学与大数据学院，安徽淮南232001)

众所周知，神经网络是一门以人脑为基础的智能科学。近年来，不同类型的神经网络模型的动力学得到了广泛研究，如双向联想记忆神经网络[1]、Hopfield神经网络[2]、细胞神经网络[3]、Cohen-Grossberg神经网络模型等，其中Cohen-Grossberg神经网络模型是在1983年由M.Cohen和S.Grossberg在文[4]中合作首次提出的。由于Cohen-Grossberg神经网络在信号处理、联想记忆、最优化问题等领域有重要作用，但在这些网络的电路实现过程中，时间上造成的延迟是不可避免的。另一方面，环境周期性的干扰、网络因老化而周期性变化、网络相对有规则的输入控制等因素使网络系数产生周期性地变化，从而对神经网络周期解的研究也引起了广泛关注[4-11]，其中，黄创霞等在文献[11]中考虑了如下具有时变时滞Cohen-Grossberg神经网络模型：

其中，i=1，2，…，n。

基于激励函数是连续的这一假设条件，他们建立了模型(1)周期解的存在性和稳定性判据。然而，正如Forti等在文献[12]中指出，在神经网络应用中，神经元之间的信号传输或神经元的信息输出往往会表现出不连续的特征。实际上，神经元根据其自身的活跃水平，对网络中其他神经元的影响存在激励、抑制，或激励、抑制、无影响状态，在众多神经网络中，这些状态之间的切换往往是不连续的。当神经网络模型(1)中的信号激励函数在不满足连续性条件下，对其周期解存在性的研究非常少见。因此，对含有时滞项的不连续激励函数Cohen-Grossberg神经网络模型动力学的研究显得尤为重要。

基于以上讨论，下面研究一类如下具有混合时滞和不连续激励函数的Cohen-Grossberg神经网络模型：

其中n是神经元的个数，xi表示第i个神经元在t时刻的状态，ai(xi(t))表示放大函数，fj(xj(t))是神经元的激励函数，bi(xi(t))表示适当的良态函数，cij(t)表示第j个神经元在t时刻的输出对第i个神经元的激励程度，dij(t)、rij(t)分别表示第j个神经元在t时刻对第i个神经元的时变时滞和分布时滞反馈，pij(s)表示分布时滞的随机核函数，τij(t)是传输时滞，Ii是网络的外部输入。

本文在摒弃激励函数连续性的前提下，利用集值版本的Mawhin重合度定理、不等式技巧，建立该神经网络周期解存在性的新结论，所获结果在较大程度上改进并推广了已有文献中的相应结论。在本文中，首先作如下假设：

(H1)cij(t),dij(t),rij(t)∈C(R,R)是以ω为周期的连续函数，i,j=1，2，…，n。

(H2)ai(u)是正的有界函数，且对∀u∈R,0＜＜ ai(u)＜＜ +∞,都是正常数。

(H3)fi在除孤立点ρki的可数集上是连续的，并在其孤立点处存在有限的左右极限fi+(ρki),fi-(ρki),此外，fi在R的任意紧区间内具有有限个间断点。

(H4)pij(s):[0,∞)→[0,∞)是可测的正规化函数，即存在σ＞0，有

(H5)bi(u)∈ C1(R,R),bi(⋅)=0有一个唯一解yi*，i=1，2，…，n。

1 预备知识

下面介绍一些文中会用到的记号、定义及引理。设向量x∈ Rn，定义xT=(x1,x2,…,xn)T为向量x的转置；给定一个集合Ω⊂Rn，[Ω]表示集合Ω的闭凸包，P(Ω)表示Ω的所有子集构成的集合，Pkc(Ω)表示Ω的所有非空、紧和凸子集的集合。对于一个定义在R上的ω周期函数g(t)，定义g+、和gˉ为

定义1[13-14]如果对包含F(x)的任一开集U(F(x))，都存在 x∈X 的邻域 V(x)，使得F(V)⊆U，称F在x∈X点是上半连续的。若F在任一点x∈X处都上半连续，则称F在X是上半连续的。

定义2[13-14]一个集值映射F:X→P(Y)，如果对于任意的x∈X，有f(x)∈F(x)，则称函数f:X→Y是F的一个选择。

由于系统(2)的激励函数满足条件(H3)，因此其右端是依赖于状态的不连续系统。为研究不连续系统(2)周期解的存在性，采取如下Filippov解的定义。

定义3 如果函数x=(x1,x2,…,xn)T满足

(1)x=(x1,x2,…,xn)T在(-∞,T)上连续，且在[0,T)的任意闭区间上绝对连续；

(2)存在一个可测函数 γ=(γ1,γ2,…,γn)T:(-∞,T)→ Rn使得γj(t)∈ -co[fj(xj(t))]，且对于几乎处处(简记为a.a.)t∈(-∞,T)，有下式成立：

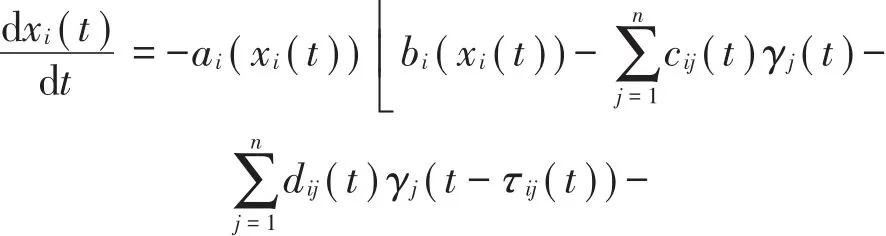
则称函数 x=(x1,x2,…,xn)T为模型(2)在(-∞,T)(T ∈(0,+∞))上的Filippov解。任何满足(3)式的函数γ =(γ1,γ2,…,γn)T为相应于x(t)的输出解，称[x,γ]为系统(2)的解。注意到上述模型(2)解的定义，意味着下列微分包含成立：

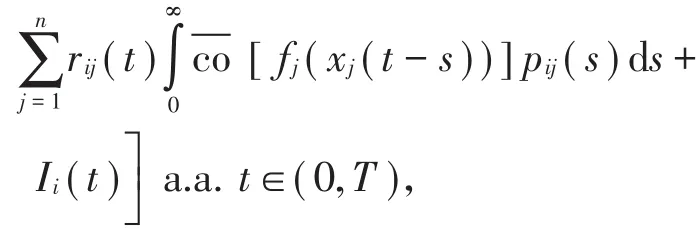
也就是说，系统(2)的状态解是系统(2)在Filippov意义下的解。

定义4(初值问题) 设连续函数φ=(φ1,φ2,…,φn)T:(-∞,0]→ Rn，以及可测函数 φ=(φ1,φ2,…,φn)T:(-∞,0]→ Rn满 足 φj(s)∈-co[fj(ϕj(t))]，对于a.a.t∈(-∞,0)。若存在常数T ＞ 0，使得在区间(-∞,T)上x为系统(2)的解，γ为相应于x(t)的输出解且

称[x,γ]:(-∞,T)→ Rn× Rn为系统(2)满足初始条件[φ,ϕ]的解。

定义5[5]如果(3)式在(0,+∞)上满足初始条件的解x(t)有x(t+ ω)=x(t),t≥ 0，则称x(t)为(3)式的ω-周期解。

引理1(集值版本的Mawhin延拓定理[15-16])设X为由所有从R到Rn上连续的ω-周期函数构成的集合，Ω⊂X为有界开集，集值映射F:R×Rn→Pkc(Rn)是上半连续的且关于t是ω-周期的。如果下列条件成立:

(a)当x ∉ ∂Ω，λ∈(0,1)时，x′(t)∈ λF(t,x)；

(b)当u∈∂Ω ⋂ Rn时，每一个解u∈ Rn都有则微分包含x′(t)∈ λF(t,x)在X ⋂上至少存在一个ω-周期解。

定 义 6[16]若 实 矩 阵 Θ=(θij)n×n满 足θij≤ 0,i,j=1,2,…,n,i≠ j，且Θ-1≥ 0，则称Θ为M矩阵。

引理2[16]设ρ(K)是矩阵K=(kij)n×n的谱半径，若ρ(K)＜1，K ＞0，则(E-K)-1≥ 0，E为n阶单位阵。

2 周期解的存在性

定理1如果假设(H1)～(H5)成立，进一步假设

(H6)对于j=1,2,…,n，使得对任意xj,u∈R，有 bj(u)∈C1(R,R),ḃj(u)＞ 0 ，且 存 在 常 数L1j,M1j,L2j,M2j,L3j,M3j，有

其中，

(H7) ρ(Κ )＜ 1，Κ =(kιj)ν×ν，D=(D1,D2,…,Dn)T，其中，kij=L2iL3j(cij++dij++rij+),

则不连续系统(2)至少存在一个ω-周期解。

证明 定义如下工作空间

显然，X在赋予范数‖⋅‖下为Banach空间。取

式中，

由(H1)易知Fi(t,x)是一个具有非空紧凸值的上半连续集值映射。

为应用引理1，首先寻求一个合适的有界开集Ω。根据微分包含

有

假设 x(t)=(x1(t),x2(t),…,xn(t))T是系统(2)对应于某个λ∈(0,1)的解，根据文献[16]中的可测选择定理知，存在可测函数γj(t)∈[fj(xj(t))]，对 a. a. t≥0 ，使 得

因为x=x(t)在[0,ω]上是连续的，所以存在ti∈ [0,ω ]，使得

因此

这意味着

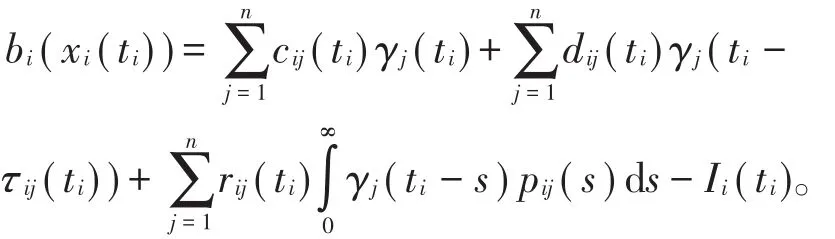
根据(H6)，(H7)可得

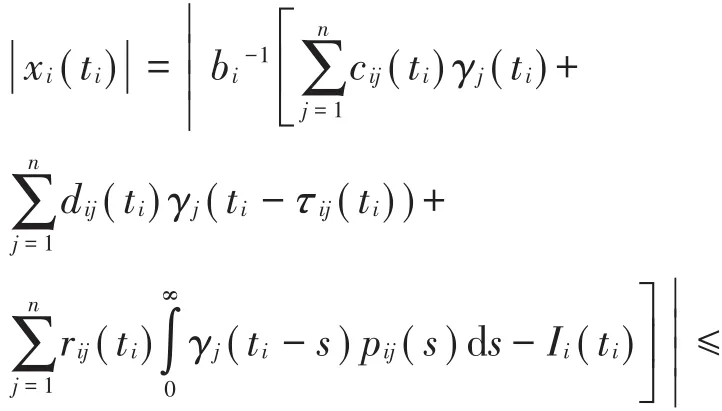
其中，kij=L2iL3j(cij++dij++rij+),

因为ρ(K)＜ 1，由引理2可知(E-K)-1D=h≥0，其中={x(t)=(x1,x2,…,xn)T, ||xi≤ hi,i=1,2,…,n}。则由(4)式可得

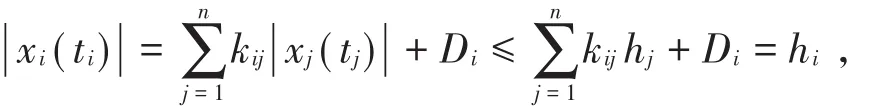
因此，可以得到

显然hi与λ 无关。令l={hi}，则存在d ＞ 1，使得dhi＞ l。对任意i=1,2,…,n，取

显然，Ω是X中的有界开集，并对∀λ∈(0,1)，当x∉ ∂Ω时，有x′(t)∈ λF(t,x)。

下面证明Ω满足引理1的两个条件:

(a)由前所述，显然成立。

(b)当u=(u1,u2,…,un)T∈ ∂Ω ⋂ Rn时，有

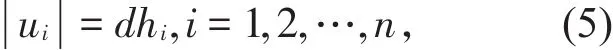
即u是Rn上的常值函数。当u∈∂Ω⋂Rn时，有下式成立：

或者

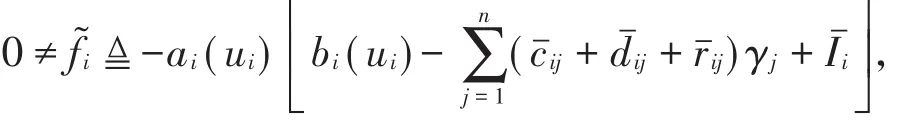
则有

否则有存在γ =(γ1,γ2,…,γn)T∈-co[f(x)]，使得 ||f͂i=0，即F (t,x)dt=f0(x)，或者等价地，

因此

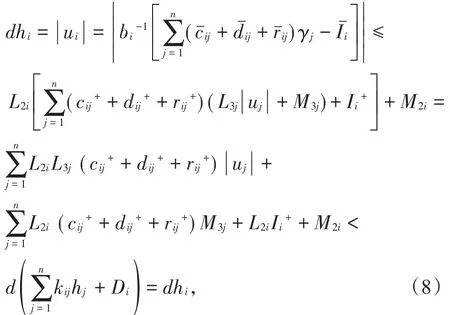
矛盾，故(6)式成立。

最后，定义如下的同伦集值映射Φ:(Ω ⋂ Rn)×[0,1]→ Ω ⋂ Rn，则

其中，(x,θ)∈(Ω ⋂ Rn)×[0,1]。

如果x=(x1,x2,…,xn)T∈ ∂Ω ⋂ Rn，则

为Rn上的常值向量。

我们断言

否则

那 么 存 在 γi∈[fi(ui)],i=1,2,…,n，使 得0 ∈ Φ(u,θ),θ∈[0,1]。因此

即(θaˉi+ai(ui)) ||bi(ui) ≤ θai(ui) ||bi(ui)+

进而有

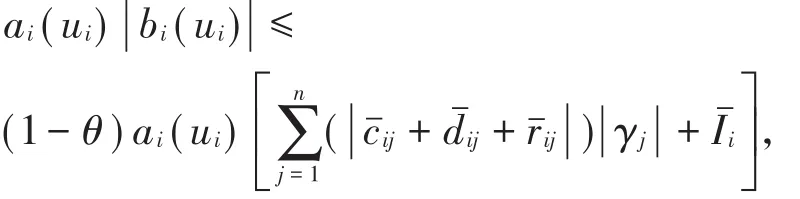
所以有

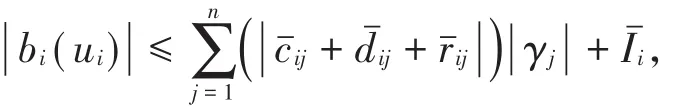
由(5)～(8)式的证明过程，同理可得

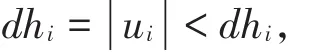
矛盾。因此，当(u,θ)∈(∂Ω ⋂ Rn)×[0,1]时，有0=(0,0,…,0)T∉Φ(u,θ)成立，从而由同伦不变性(H5)知

综上所述，Ω满足引理1的所有条件，则系统(2)至少有一个ω-周期解。

3 应用举例

考虑如下具有混合时滞和不连续激励函数的Cohen-Grossberg神经网络：

显然，

考虑如下不连续激励函数

取τij=1,rij=0,i,j=1,2，从而

容易计算ρ(K)≈0.716。这意味着定理1的条件全部满足，所以系统(9)至少存在一个2π-周期解。

4 结论

本文所考虑的不连续Cohen-Grossberg模型(2)不仅具有离散时滞，同时具有分布时滞，具有一般性。又由于所考虑模型的激励函数是不连续的，为克服激励函数的不连续性所带来的理论和技术上的困难，本文利用微分包含理论及不等式技巧研究了不连续模型(2)周期解的存在性，从而已有文献[7-11]及其参考文献中有关连续情形下周期解存在性的结论不适应于不连续神经网络(9)。因此，本文的结论改进和推广了已有文献的相应结论，为工程技术工作者提供了理论依据。