优化初始聚类中心的改进K-means算法

唐东凯，王红梅，胡 明，2，刘 钢

1(长春工业大学 计算机科学与工程学院，长春 130012) 2(长春工程学院，长春 130021) E-mail：wanghm@ccut.edu.cn

1 引 言

聚类的目标是最大化同一个簇中数据对象的相似程度，并使不同簇中的数据对象的相似程度最小[1].根据聚类过程的不同，Han[2]等人，将聚类分成基于密度、基于划分、基于模型、基于网格、基于层次的五种聚类模型.K-means算法最早由MacQueen[3]提出，是基于划分模型中的一种，因其计算简单、容易理解而被广泛应用.

随机选取初始中心点的方法，使得K-means算法易陷入局部最优解，且聚类结果不稳定.针对这一缺点，众多学者提出了许多优化初始中心点的选择方法.Arthu[4]等人提出了K-means++算法，该算法首先在数据集上随机选取一个数据对象作为第一个初始中心点，再在剩余的数据对象中，计算到已有初始中心点的欧式距离，选择距离值最大的数据对象作为第二个初始中心点，重复上述过程，直到选出k个初始中心点为止.文献[5,6]引入智能算法的思想，在每次迭代计算初始中心点的时候分别使用粒子群算法和遗传算法来迭代寻找最优解，选取使误差平方和最小的数据对象作为初始中心点.成卫青[7]等人首先在数据集中选取两个距离最远的数据对象，其次再选取分别与这两个数据对象距离最近的两个数据对象作为初始中心点，使用K-means算法进行聚类，对聚类效果最差的那个簇，使用上述方法选取新的初始中心点，最后进行聚类.一些学者从数据对象的密度特征出发[8-10]，文献[8]按照密度聚类的思想首先计算出每个数据对象的密度值，然后在高密度值的数据对象中选取相互距离最远的数据对象作为初始中心点.文献[9]也是先计算出每个数据对象的密度值，找出距离最高密度值最近的数据对象，然后用这两个数据对象的中点作为第一个初始中心点，并以此为中心，以样本间的平均距离为半径画圆，删除在同一个圆内的所有数据对象，在剩余的数据对象中按上述方法继续选择初始中心点直到k个为止.文献[10]以样本的方差作为启发信息，样本间的平均距离作为半径，在该区域选取方差最小的样本作为初始聚类中心.

K-means算法易受离群点的影响，离群点的存在往往会影响初始中心点的选取，增加迭代次数，导致较差的聚类结果.对这一问题，冷泳林[11]等人首先使用基于距离的离群点检测算法找出数据集中的离群点，在选择初始中心点时避免选择离群点作为初始中心点，只在非离群点中进行随机选取.

在上述算法中有的解决了K-means算法随机选取初始中心点的问题，但却忽略的离群点对结果的影响，比如文献[4-6]；有的虽然避免了离群点的影响，但最后还是随机选取初始中心点，比如文献[11].因此，针对K-means算法的两种不足，本文使用离群因子来排除离群点的影响，最大最小算法来避免随机选取初始中心点，提出了一种基于离群因子和最大最小算法的优化K-means初始中心选择算法，即OFMMK-means算法(K-means algorithm based on Outlier Factor and Maximum and Minimum distances).实验表明，在时间基本相同的情况下，OFMMK-means算法相比K-means算、K-means++算法，具有更好的聚类效果和较高的稳定性，另外还具有较少的迭代次数.

2 K-means算法

K-means算法核心思想是：设数据集含有n个数据对象，首先从这n个数据对象中随机选取出k个对象作为初始聚类中心，对于剩余的对象根据每个数据对象与k个聚类中心的相似程度将其分配到最相似的簇中，然后对于每一个簇，将簇中的所有对象的平均值作为新的聚类中心，进行下次迭代.不断重复该过程，直到簇中心不再发生变化，准则函数收敛，准则函数如公式(1)：

(1)

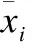
K-means算法初始聚类中心的选取是随机的[12]，这样容易造成聚类结果不稳定，且易陷入局部最优.另外，由于样本中可能含有噪声或者离群点，聚类中心对其比较敏感，也很容易导致较差的聚类结果.

3 OFMMK-means算法

OFMMK-means算法对于初始中心点的选取主要分三个过程：1)对数据集先进行基于密度的离群点检测，计算出每个数据对象的离群因子；2)根据离群因子的大小对数据集进行升序排列；取前α*n(0<α≤1，n为样本集的大小)个数据对象作为初始中心点的候选集；3)在候选初始中心点集上根据最大最小算法，选取距离最远的数据对象作为初始中心点.下面分别对这三个过程进行介绍.

3.1 计算离群因子

K-means算法在随机选取初始中心点时，如果数据集中存在离群点或噪声，很容易使初始中心点偏离最优的聚类中心，降低聚类精度.所谓离群点是指明显偏离数据集中其他对象的数据点.离群点检测方法可以发现数据集中小部分偏离大多数数据行为或数据模型的异常数据，可以避免离群点对聚类的影响[13].

本文使用基于密度的离群点检测算法-LOF算法[14]来计算数据对象的离群因子.离群因子的大小反映了数据对象的偏离程度，离群因子越大，则说明其偏离程度越高，越有可能是离群点；反之，离群因子越小，则说明它周围的数据对象越多，其密度越大，越有可能是中心点.所以OFMMK-means算法使用离群因子来限定初始中心点的选取范围，选取那些离群因子小的数据对象作为初始中心点可以更切合中心点的实际情况.下面介绍一下LOF算法中涉及的基本概念.

定义.对象p的第k距离(k-distance of an objectp).

对于一个正整数k，数据对象p的第k距离记为k-dis(p).在数据集D中，存在一个数据对象o，该数据对象与数据对象p之间的距离记作d(p，o).满足以下条件，则取k-dis(p)等于d(p，o)：

1)至少存在k个数据对象o′∈D/{p}满足d(p，o′)≤d(p，o)；

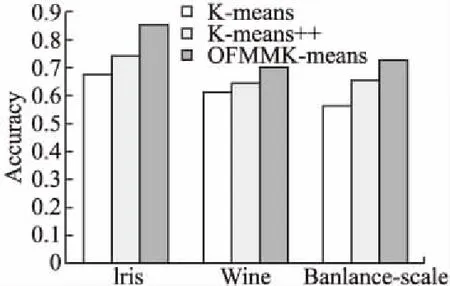
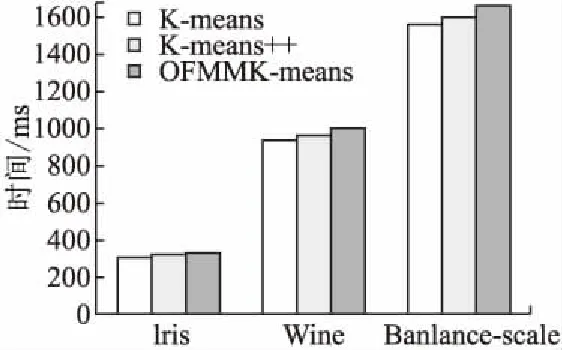
2)至多存在k-1个数据的对象o′∈D/{p}满足d(p，o′)

该定义通过考察每一个数据对象与被考察对象之间的距离，并找出其中数值上为第k大的那个距离.根据定义，可进行离群因子的计算，以对象p为例：

第1步.构建对象p的第k距离邻域

对象p的第k距离邻域是指小于等于对象p的第k距离内的所有对象组成的集合.计算公式如(2).实际上该集合反映了数据对象的偏离程度，可以设想，如果该集合比较大，则说明该对象的第k距离邻域比较大，则它的偏离程度就比较大，反之，若集合较小，则偏离程度就小.

Nk(p)={o∈D/{p}|d(p，o)≤k-dis(p)}

(2)

其中，d(p，o)表示数据对象p和数据对象o之间的欧式距离；k-dis(p)表示对象p的第k距离(见定义).

第2步.计算对象p的局部可达密度.

由第1步得出的对象p的第k距离邻域，进而计算p的局部可达密度，对象p的局部可达密度是指对象p的Nk(p)内的所有对象的平均可达密度的倒数，具体计算公式如(3)：

(3)

考虑这样一种情况，如果至少有k个对象和p有相同的坐标值，却是不同的数据对象，那么公式(3)的分母就会趋近于0，而对象p的局部可达密度将趋于∞，相反如果数据对象p距离聚类簇较远，相应的lrdk(p)值则较小.

第3步.计算对象p的离群因子.

结合公式(2)和(3)来计算p的离群因子，公式如下(4)：

(4)

分析公式(4)可知，LOFk(p)的大小反映的是数据对象p的第k距离范围之内的空间点的平均分布密度，容易看出，若p的局部可达密度越小，p的Nk(p)内的对象可达密度越大，那么对象p的LOF值就越大.也就是说，一个对象的LOF值越大，那么该对象是离群点的概率也就越大.

综合上述三步，可计算出数据集中的每个对象的离群因子，根据离群因子的大小可以知道离群点的分布情况，再进行初始中心点的选取时，就可以避免离群点的影响.

3.2 生成初始中心点候选集

3.1小节得出了数据集上每个数据对象的离群因子，离群因子的大小反映了该数据对象是中心点的可能性大小.也就是说，一个对象的离群因子越小，在实际聚类中，就越有可能是中心点；相反，那些离群因子大的对象，其偏离中心点的程度也就越大，在选择初始中心点的时候，就应该避免选择这样的对象.

OFMMK-means算法产生候选初始中心点集的步骤：

第1步.根据3.1节计算出数据集D中每个数据对象i的离群因子LOFk(i)；

第2步.对数据集D按离群因子的大小，进行升序排序，并记为DL；

第3步.在DL上，选取前α*n(0<α≤1，n为数据集的大小)个数据对象作为候选初始中心点集，记为DCL.

OFMMK-means算法在产生候选初始中心点集时，在第三步引入了一个取样参数α，α的取值过小，可能导致初始中心点集中在一个簇中，导致迭代次数增加，聚类效果较差.α取值过大，也容易选出较差的初始中心点.所以，α的取值本文通过实验来确定.

3.3 选取初始中心点

OFMMK-means算法使用距离尽可能远的数据对象作为初始聚类中心点，可以避免初始聚类中心过于邻近的情况，这样数据集能得到较好的划分.Katsavounidis[15]等人于1994年提出最大最小法，它是聚类算法中初始聚类中心点的选择方法之一.最大最小算法的初始中心点如公式(5)：

Ci=max{Disj;j=1，2，…，n}

(5)

其中，Disj数据对象j到中心点的最小距离；n为样本个数；Disj的计算方法如公式(6)所示：

(6)

其中，C表示初始中心点集合；d(Ci，xj)为数据对象xj到初始中心Ci的欧式距离.

OFMMK-means算法使用最大最小距离来选取初始中心点，其过程描述如下：

Input：数据集D，聚类个数k

Output：k个初始中心点

Step1.令C=Ø，在D中随机选取一个对象作为第一个初始中心C1，C={C1}；

Step2.在D剩余数据对象中，计算每个对象与C1的欧氏距离，选取值最大的那个作为第二个初始中心C2，C={C1，C2}；

Step3.repeat

对于xj(xj∈D/C)(j=1，2，…，n)按照公式(6)计算xj到初始中心的最小距离；

按照公式(5)，选出最大距离的对象作为Ci，C={C1，C2}∪{Ci}；

untili>k

Step4.输出k个初始中心点.

OFMMK-means算法使用最大最小算法来选取初始中心点，可以避免初始中心点位于相同簇中，可以减少迭代的次数.

3.4 OFMMK-means算法描述

综合上述3个过程，下面给出OFMMK-means算法的整体描述：

Input：数据集D，聚类个数k，取样比例α

Output：完成聚类的k个簇

Step1.对D中的每一个数据对象，根据3.1小节离群因子的计算过程来计算每个对象i的离群因子LOFk(i)；

Step2.根据离群因子的大小，按照3.2小节产生候选初始中心点集DCL；

Step3.使用数据集DCL作为3.3小节中最大最小算法的输入数据集，并按最大最小算法过程选出k个初始中心点；

Step4.从Step3中得到的k个中心点出发，执行K-means算法，得出聚类结果.

为了去除离群点，OFMMK-means算法根据离群因子的大小对数据集进行升序排列，并产生包含中心点的候选集，之后在候选集上根据最大最小距离来排除两个初始中心点位于相同簇中的可能.则OFMMK-means算法减小了K-means算法对初始中心点敏感的程度.

4 实验结果与分析

为了验证本文算法OFMMK-means的有效性，选取UCI机器学习数据库上的Iris、Wine、Balance-scale这3个基准数据集作为测试数据集.本文使用Python来实现所提出的算法以及涉及的相关算法，语言版本为Python2.7.0.运行环境为：Intel(R)Core(TM) i5-3470 CPU，3.20GHz，8.00GB，操作系统是Windows8.1系统，64位.

三个测试数据集的统计信息如表1所示：

表1 测试数据集信息Table 1 Details of test data

4.1 验证参数α的取值

聚类结果用准确率作为评价指标，实验4.2和4.3采用相同的评价标准.设样本集D包括k个类，聚类准确率的表示如式(7)所示：

(7)

其中，ai表示被正确划分到类Ci中的样本数；|D|表示样本总数.

OFMMK-means算法比K-means算法多了一个参数α，α的大小决定初始中心点的选择范围的大小，因此α的取值要适当.本文将在上述三种测试数据集上使用OFMMK-means算法进行聚类，并验证α的取值，如图1所示.

从图1中可以看出，在前半部分，三种测试集的聚类精度随着α值的增大而增大，在α取0.4左右时，达到最大值.当α值继续增加时，聚类精度开始下降，这是因为候选初始中心点集变大，选择范围变大.值得注意的是，当α取值为1时，OFMMK-means算法已完全退化，相当于在全部测试数据集上，选取k个距离较远的数据对象作为初始中心点，这过程和K-means++算法相同.

4.2 验证OFMMK-means算法的有效性

本文的对比算法是K-means算法、K-means++算法以及本文算法OFMMK-means算法.三种算法分别在三种测试数据集上分别运行10次，取聚类精度的平均值作为最终结果.另外，根据实验4.1，OFMMK-means算法中的参数α取0.4.

图2显示的是三种算法的聚类精度.首先从图2中可以看出，在三种测试数据集上，OFMMK-means算法的聚类精度均高于其余两种算法.也可以看出，K-means++算法优于K-means算法，这是因为K-means++算法的初始中心点不再是随机选取的，而是根据最大最小算法思想选取距离相对较远的数据对象作为中心点.但是它并没有考虑到离群点对聚类结果的影响，可能会选择距离较远的离群点作为初始簇心，所以相较于排除离群点的OFMMK-means算法来说，其聚类精度稍低.图3是三种算法在测试数据集上的运行时间.从图3可以看出，OFMMK-means算法在三种数据集上执行时间与其他两种算法的执行时间基本相同，差距不大.图2和图3分别从准确率和运行时间上验证了OFMMK-means算法的有效性.

图1 α值对准确率的影响Fig.1 Effect of α on accuracy

图2 三种算法在测试数据集上准确率Fig.2 Accuracy of the three algorithms on the test data set

图3 三种算法在测试数据集上的运行时间Fig.3 Time of the three algorithms on the test data set

4.3 验证初始聚类中心对聚类精度的影响

K-means算法易受初始中心点的影响，不同的初始中心点，最终的聚类精度也会不同.由于篇幅限制，只给出K-means算法、K-means++算法和OFMMK-means算法在Iris数据集上的详细情况，如表2所示，三种算法分别共运行了20次，并给出了每次运行时所选取的初始中心点(用其编号表示)、迭代次数、准确率和运行时间(单位为ms).

表2 三种算法在Iris测试数据集上的详细结果Table 2 Results of the three algorithms on the Iris test data set

从表2中可以看出，K-means算法和K-means++算法的平均准确率分别是72.24%和75.94%，而OFMMK-means算法的平均准确率比K-means算法高了12.68%，比K-means++算法高了8.98%，达到84.92%.并且从20次的运行结果看，K-means算法和K-means++算法最坏情况下准确率是52.67%，最高是89.33%和90.03%，聚类结果非常不稳定.而OFMMK-means算法的20次运行结果都相对稳定，且最高准确率为91.67%.因此，从聚类精度上看，OFMMK-means算法具有较高的聚类精度和较好稳定程度.从运行时间上来看，OFMMK-means算法比其他两种算法执行时间略高，是因为OFMMK-means算法在聚类前需要算出每个对象的离群因子，但是因为优化了初始中心的选择，K-means算法和K-means++算法的平均迭代次数分别是6.7和5.6，OFMMK-means算法的平均迭代次数是5.1，OFMMK-means算法具有较小的迭代次数，从而20次运行时间的均值与其他两种算法相差不多，不到1秒，基本相同.

5 结 论

针对K-means算法对初始中心点比较敏感且易受孤立点影响的缺陷，本文首先引入基于密度的离群点检测算法，来消除孤立点对聚类结果的影响.其次，根据每个对象的离群因子的大小对样本集进行升序排列，保证了中心点位于较前的位置，并产生候选初始中心点集，随后根据最大最小算法，在候选初始中心点集中选取离群因子较小且相对距离较远的数据对象作为初始中心点，跳出了K-means算法的随机选择策略，保证了聚类结果的稳定性.实验表明，在时间基本相同的情况下，相对于K-means算法和K-means++算法，本文提出的算法OFMMK-means具有较高的聚类准确率和较好的稳定性，并且对于聚类的平均迭代次数，OFMMK-means算法的平均迭代次数也较小.因此，本文提出的聚类算法是有效的、可行的.