中国PPI与CPI的非对称Granger因果关系：基于时频域的研究

苏 阳,王 璐,田海涛,马元慧

(西南交通大学 数学学院，四川 成都 611756)

居民消费者价格指数(consumer price index，CPI)和生产价格指数(producer price index,PPI )的作用关系与传导机制一直是宏观经济研究的核心问题[1],厘清两者之间的关系，对于预测通货膨胀，管理通胀预期[2]，实现隐含的通货膨胀目标等都是至关重要的[3]。理论上来看，从需求角度考虑，CPI通过流通领域影响PPI；从供给方向考虑，PPI的变动必然会顺着产业链传递到服务项目上，进而显著影响CPI。但是，由于存在经济环境不同、通胀风险的不确定性等问题，CPI和PPI之间的波动方向和程度之间也存在某种不确定的先后顺序和传导关系，因此当前国内外学者仍然没有对二者关系形成统一意见。

CPI和PPI之间存在着单向引导关系这一实证结果较早来自于CLARK[4]的研究，其从资本的重要性、提高生产率及维持和扩大消费群体等角度考虑，认为PPI上涨并不一定会导致CPI上涨，而PPI的波动只可以将弱效应传递给CPI。同时，通过对美国CPI和PPI数据进行检验，发现PPI不能系统地预测CPI；贺力平等[5]探究了中国PPI与CPI的Granger因果关系，实证结果显示CPI是PPI的Granger原因，后者经过1～3个月左右的时滞对前者的变动作出反应；TIWARI[6]利用频域方法探讨了澳大利亚PPI与CPI之间的Granger因果关系，表明CPI在中等水平频率Granger导致PPI，并提供中等周期的证据，反之PPI不会在任何频率水平上引起CPI的变化。

然而，CPI和PPI之间存在着双向因果关系这一实证结果较早来自于COLCLOUGH等[7]的研究，认为从需求方面考虑，CPI和PPI之间存在双向因果关系也是合理的，并提供了CPI和PPI之间存在双向关系的证据。徐伟康[8]利用前人的数据，通过建立VEC模型得到了在短期和长期内CPI和PPI互为彼此的Granger原因的结论。同时，张成思[9]对VECM模型进行实证研究，得出上游价格对下游价格具有显著的动态传递效应，而下游价格对中游价格、中游价格对上游价格也存在反向的反馈效应，从而CPI和PPI之间存在双向的Granger因果关系。

目前，研究CPI与PPI之间的因果关系主要使用传统Granger检验方法。但是这种方法存在的问题是其假设了正冲击(positive shock)和负冲击(negative shock)导致的因果影响是对称的，学者们并没有将正负冲击彼此分开考虑。显然，投资者或消费者通常对正冲击和负冲击的回应是相反的，因此这可能是一个太过于严格的假设。同时AKERLOF 等[10-11]普遍认为存在信息不对称的市场。鉴于此，为了将正负冲击造成的影响分开进行考虑，HATEMIJ[12]在时域上提出非对称Granger检验方法，该方法的优点在于将正负冲击分开，能够充分考虑到CPI波动与PPI波动之间的因果关系，有效克服了由于CPI与PPI波动存在的混合效应而导致结果不明确的缺点，更有利于精确得到CPI波动与PPI波动之间的Granger因果关系结论。不仅如此，以往的研究大多都停留在时域上面，其局限性在于只能得出在整个时间区间上的Granger因果关系，但是Granger因果关系的强度和方向可能随着频率的不同而发生变化，因此笔者引入非对称Granger检验方法，进一步将BAHMANI-OSKOOEE等[13]提出的在频域上的非对称Granger因果检验，用于探究CPI与PPI在频域的非对称Granger因果关系。

1 基于时域的非对称Granger因果检验

文献[12]首次提出将正负冲击分离出来进行研究，在时域上提出非对称Granger因果关系。假定存在协整变量Xt与Yt，滞后阶数均为T，y10与x10分别为序列的初始值，显然有：

(1)

(2)

(3)

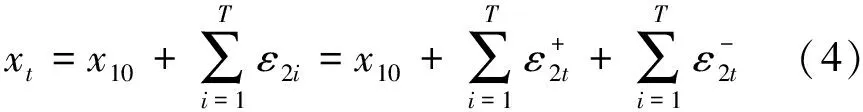
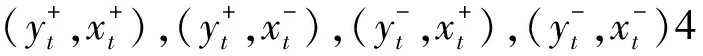
(5)

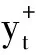
采用文献[12]提出的HJC准则选定最优的滞后阶数m，如式(6)所示。

(6)

式中：|Ω|为基于滞后阶数j的VAR模型中误差项的估计方差-协方差矩阵；n为VAR模型的方程数；T为观察变量的个数，使式(6)达到最小时的j值即为选定的最优滞后阶数m。

Y=DZ+δ

(7)

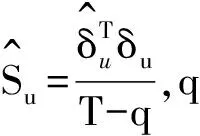
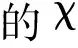
2 基于频域的非对称Granger因果检验

文献[12]提出的非对称Granger检验在时域只能得到整个时间段上的非对称Granger因果强度，但是其强度和方向却可能随频率的不同而变化，通过频域上的检验能够得出在具体频域段Granger因果强度，进一步得出预测周期的长短。因此文献[13]将非对称Granger因果检验理论从时域推广到频域上，其变量的正冲击和负冲击定义与时域上的一致。

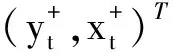
(8)

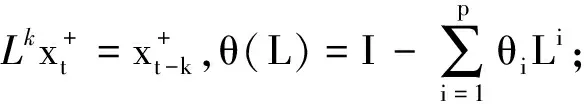
(9)

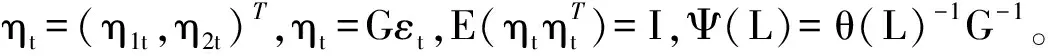
(10)

其中，w表示频率。

文献[14]提出在频域上的因果关系定义如式(11)所示。

(11)

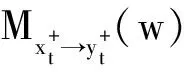
(12)

式(12)的充分必要条件是：

(13)

(14)

除式(8)的VAR模型外，文献[15]建议选用下列VAR模型：

(15)

令:

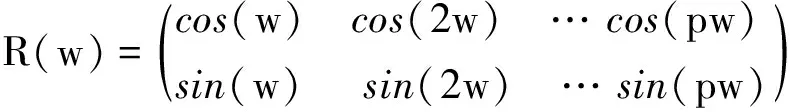
(16)

θ12=(θ12,1,θ12,2,…，θ12,p)T

(17)

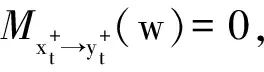
原假设H0是以原始的Wald统计量作为检验统计量，其服从自由度为2的卡方分布，自由度2为w∈(0,π)的限制条件个数。文献[12]指出金融时间序列大多数具有非异方差性，不服从正态分布，这将导致Wald检验统计量偏离其渐进分布。因此笔者将继续采用在时域基础上改进的bootstrap模拟方法，具体步骤如下：

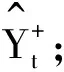
3 实证研究

笔者选用中国2006年1月—2017年9月的PPI和CPI的月度数据进行分析，数据均来源于国家统计局。由于数据的平滑和季节调整处理常导致序列之间的冲击效应减弱，可能引起数据冲击的具体时间点对后续时间的变动产生影响，因此笔者不对数据进行平滑和季节调整处理。PPI和CPI的对数序列变化趋势图如图1所示，可以看出二者在长期内具有均衡的变化趋势。

PPI和CPI对数序列的描述性统计量如表1所示，从JB统计量可以看出序列均是非正态分布，而且其斯皮尔曼等级相关系数高达0.582。这些都初步显示了PPI与CPI之间存在某种共同变化的特征。

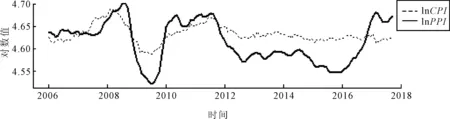
图1 数据变化趋势图

平均值中位数最大值最小值标准差偏度峰度JB相关系数ln CPI4.6324.6304.6894.5870.0200.5683.4928.997ln PPI4.6144.6224.7014.5200.047-0.0831.8747.613〛0.582

首先对带有截距项和带有截距趋势项的原始、正冲击、负冲击以及各自的一阶差分序列进行平稳性检验。PP单位根检验结果如表2所示。单位根结果表明对于给定的显著性水平5%，各项水平序列显著接受原假设，而一阶差分序列均拒绝原假设，因此各序列都是I(1)，即为I阶单整序列。利用ENGLE等[16]提出的协整检验法可得两者是非协整的关系。应该注意的是，此处的协整关系并非是进行Granger因果检验的必要条件，为了解决此问题，TODA等[17]提出在模型中加入一个额外的无约束的滞后项即可，此处不再赘述。

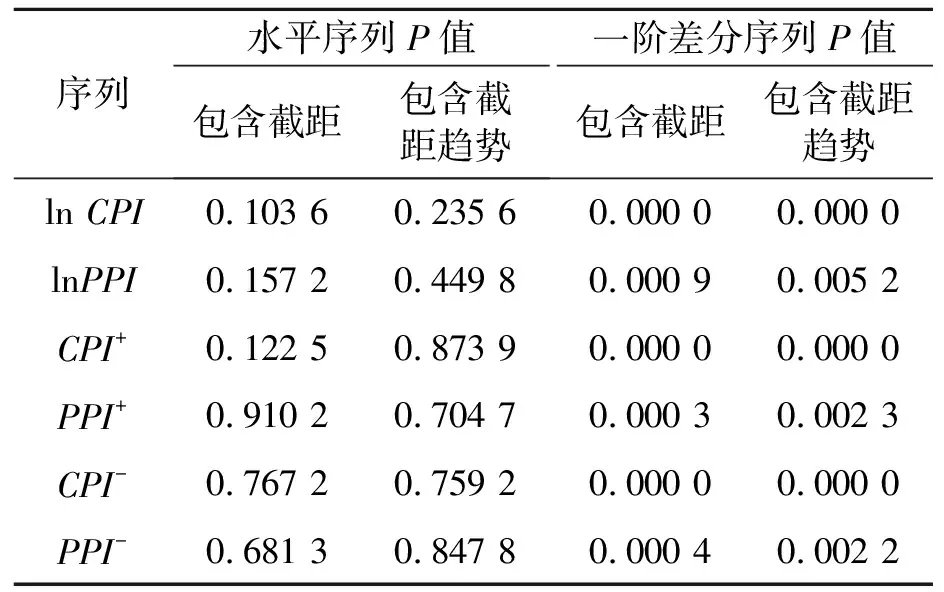
表2 PP单位根检验结果

注：原假设表示序列有一个单位根

序列多变量ARCH效应与正态性的P值检验结果如表3所示，通过HACKER等[18]提出的多元LM检验方法可以检验序列异方差性，检验多元正态性采用DOORNIK等[19]提出的多元正态性检验方法。VAR模型的最优滞后阶数通过HJC准则确定。结果显示残差序列不服从正态分布，并且ARCH效应的确存在，因此笔者将采用bootstrap模拟方法得出检验统计量的经验分布函数，从而可得到1%、5%、10%的临界点。

基于时域的传统Granger因果检验的结果如表4所示。实证结果显示PPI与CPI互为Granger原因。虽然PPI也是CPI的Granger原因，但是其强度远小于从CPI到PPI方向上的强度。

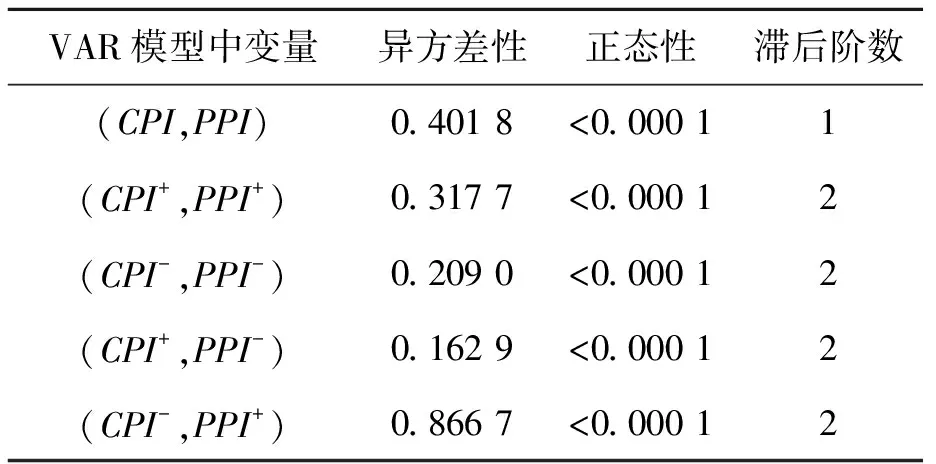
表3 正态性和ARCH效应检验结果

注：原假设分别为序列存在多元ARCH效应和序列服从正态分布

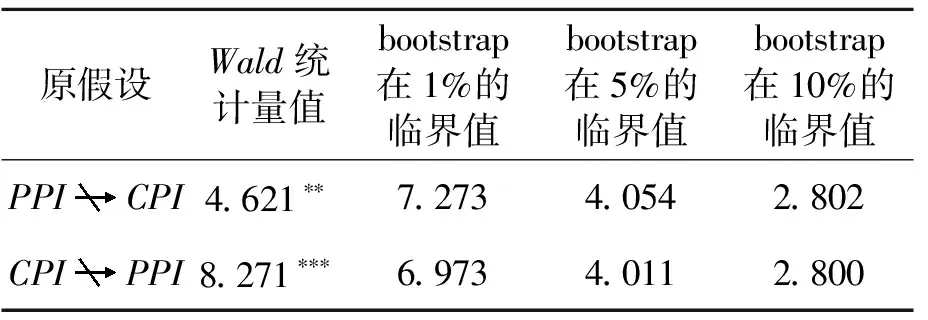
表4 基于时域的传统Granger因果检验的结果

基于时域的非对称Granger因果检验的结果如表5所示，实证结果显示CPI-与PPI-互为彼此的Granger原因，只是从CPI到PPI方向上的Granger强度较弱于从PPI到CPI的方向上，显然CPI的减少与PPI的减少之间存在互相预测的信息。与时域上传统Granger因果检验的结果相比，CPI与PPI之间的Granger因果关系体现在CPI-与PPI-上，而非整体的CPI与PPI之间的Granger因果关系。

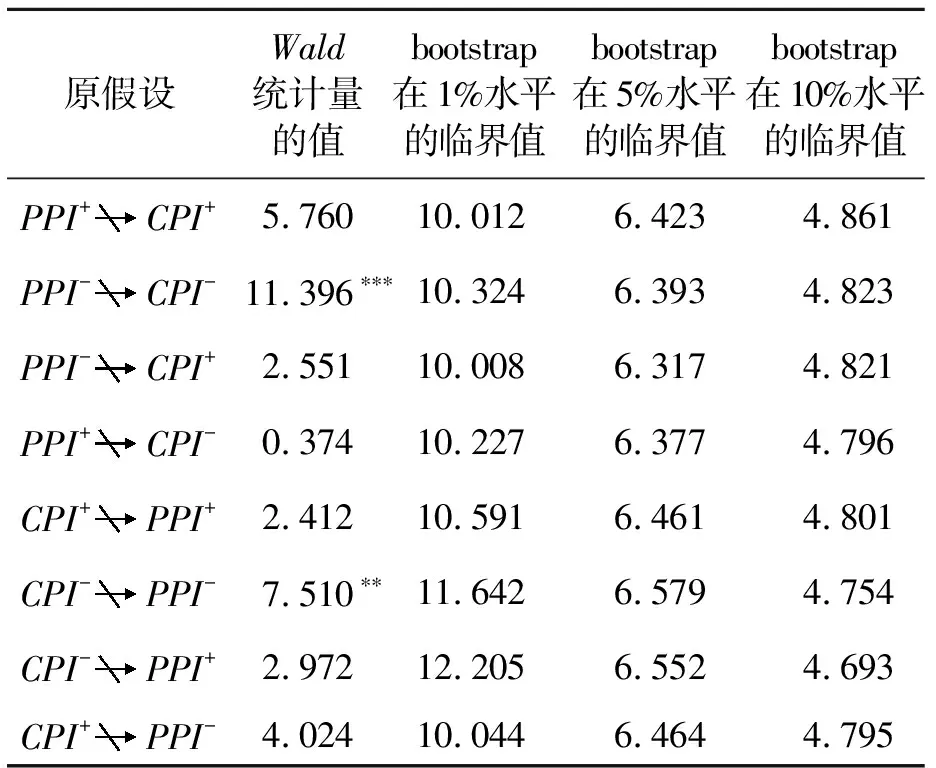
表5 基于时域的非对称Granger因果检验的结果

下面进行频域上的Granger因果检验分析。频率w可以通过T=2π/w转化为周期T。Wald统计量是衡量在给定方向上、给定频率x的Granger因果强度。因此，在频率x上Wald统计量的值越大，预测能力就越强，如果这个值高于5%水平的临界值，就认为是显著的“Granger原因”。

基于频域的传统Granger因果检验结果如图2所示。实证结果表明在频率为0.00～0.57和1.77～3.14时，即11个月以上和2～4个月内，PPI是CPI的Granger原因。PPI可以对CPI做长期或者短期预测，而CPI仅在频率为0.00～0.91，即7个月以上时，CPI是PPI的Granger原因，所以CPI可以对PPI做长期预测。

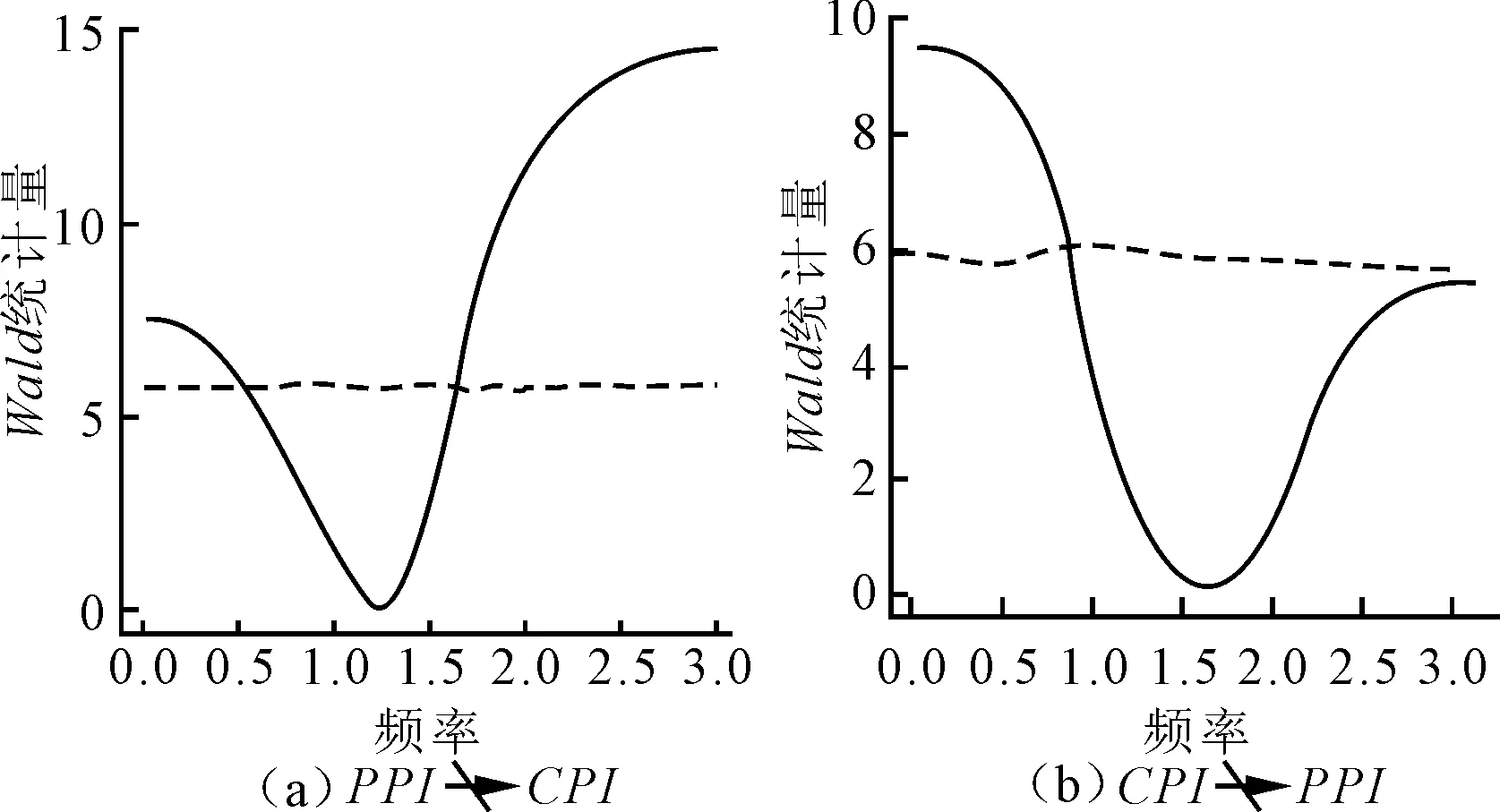
图2 基于频率w∈(0,π)传统Granger因果检验结果注：实线表示Wald统计量，虚线表示数据计算的Wald统计量

基于频域的非对称Granger因果检验结果如图3所示。实证结果表明：从PPI到CPI的方向上，在频率0.20～1.00和1.66～3.14以上时，即在6～31个月和2～4个月时，PPI-是CPI-的显著Granger原因，因此PPI-有助于提高CPI-的短期和长期预测。对于约1.71的高频，随着频率的增大，预测的强度越大。其次，在频率约为0.00～0.29时，即在10个月以上时，PPI-是CPI+显著的Granger原因，随着频率的增大，预测强度随之降低，直至没有预测作用。

从CPI到PPI的方向上，在频率为0.00～1.33时，即在5个月以上，CPI-是PPI-显著的Granger原因,CPI-可以有助于提高对PPI-的长期预测。随着频率逐渐增大，预测强度降低。在频率为0.00～0.42时，即在15个月以上，CPI-是PPI+显著的Granger原因，所以CPI-有助于提高PPI+的长期预测。在低频时，当频率从0.00增大至0.42时，预测的强度随之先增加后降低，直至频率大于0.42后没有预测作用。在频率为0.00～0.69时，即在9个月以上，CPI+是PPI-显著的Granger原因，CPI+有助于提高PPI-的长期预测，当频率从0.00增大至0.69时，预测的强度随之先增加后降低，直至频率大于0.69后没有预测作用。其他情况均接受原假设，即表明两者之间不存在非对称Granger关系。

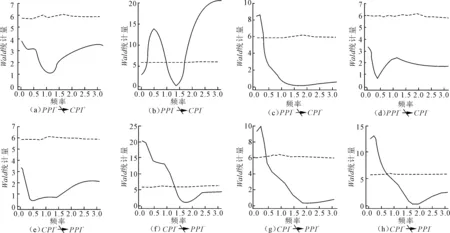
图3 基于频域的非对称Granger因果检验结果注：实线表示Wald统计量，虚线表示数据计算的Wald统计量

4 结论

笔者利用时频的非对称Granger因果检验分析了CPI和PPI的Granger因果关系，并与传统Granger因果检验做了对比。笔者的主要工作及研究成果如下：

(1)有别于传统Granger因果检验，笔者采用将正负冲击分离的非对称Granger因果检验，旨在避免正负冲击混合导致的结果不明确，以及因检验统计量可能偏离原有分布而导致的临界值发生极大差异，以上潜在的问题都可能导致所得结论与实际情况之间存在巨大偏差。

(2)由于国内经济、政治和环境因素等的错综复杂，CPI与PPI之间的Granger 因果关系尚未呈现出简单、统一的理想化形式，但整体上仍存在一定的统计规律。笔者研究结果表明：两者既存在长期内CPI-向PPI-的传导、CPI-向PPI+的传导、CPI+向PPI-的传导及PPI-向CPI+的传导，也存在短期和长期内PPI-向CPI-的传导。

(3)结合经济理论和宏观政策分析，以上实证结果基本与我国近年来经济环境和宏观调控对价格波动及传导关系产生的影响一致。由于日益增长的投资需求和出口需求，包含诸多生产资料的PPI中首先体现出巨大的资源瓶颈约束，进而在短长期内影响CPI的变动过程。同时，由于CPI包含许多易受短期波动影响的成分，如食品和能源等，这必然导致PPI产生长期波动，所以CPI波动时必然导致PPI波动。

PPI与CPI的非对称性Granger因果关系是不可忽视的。当CPI、PPI急剧波动的时候，政策制定者可以根据二者的非对称的动态时效与量化驱动程度来确定未来政策走向，充分重视PPI波动与CPI波动的传导和预警作用，实现有效的前瞻性政策调控目标，及时做出预测调整，以便采取更好的措施去把控市场。这有利于提高省市乃至中央价格调控的灵活性和价格政策的针对性和有效性，使各省市乃至中央经济决策者更有效地制定宏观经济政策。

但实证分析是针对特定时期范围(样本时间区间)内的特定数据集而得到的结论，其肯定会受到必然或偶然因素的综合影响，还需要通过理论联系实际进行更深入的剖析和探讨。