对话教学：构建数学课堂的新样态

江苏南京市宝船小学（210036）

对话教学，指在教学过程中师生双方围绕共同的学习主题，通过积极的、富有创意的交流互动，不断发现和探索教学中存在的问题，实现对问题的解决和知识的建构的过程。弗莱雷提出：“没有了对话，就没有交流，没有了交流，也就没有真正的教育。”

对话教学，积极寻求重建数学课堂文化的路径，营造良好的数学课堂文化氛围，创造充满生命力的学习乐园。

对话教学把课堂看作是促进生命发展的生态系统。数学学习内容、媒介信息、情感态度等，都在这个系统中外显为师生对话、生生对话、生本（文本）对话、自我对话，一起讨论、交流、碰撞、激励、共享……

一、创设情境，让学生乐于表达

在对话课堂里，教师和学生的角色定位发生了变化，教师从知识的传授者向学习的组织者转变；学生不只是接受者，还是学习的设计者和参与者，二者的角色在“学习共同体”的动态平衡中实现转换。对此，教师要善于给学生创设有效的问题情境，激发学生的探究欲望，鼓励学生自主探索和合作交流，让课堂成为充盈信任、愉悦和智慧的乐园。

例如，教学“认识一个整体的几分之一”时，教师创设了这样的情境：

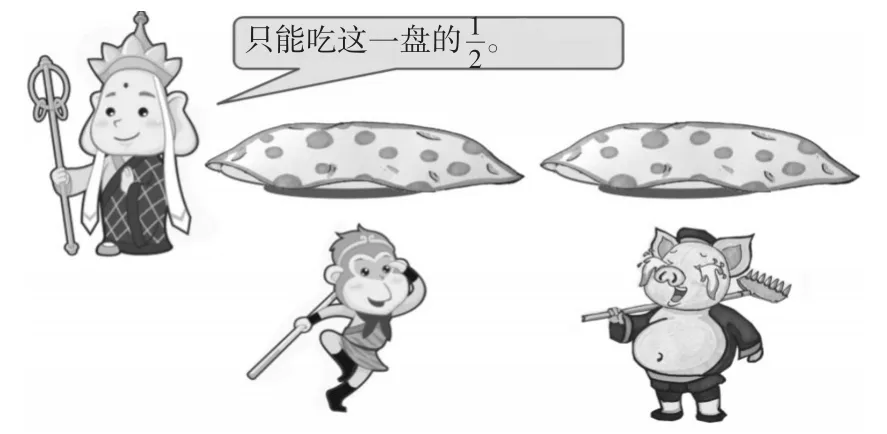
图1

师（出示图1）：唐僧拿出两盘桃，请孙悟空和猪八戒吃，并要求只能吃每盘桃的1/2。两个徒儿迫不及待地各抢了一盘，可是打开一看，猪八戒却哇哇大哭起来。想一想，这是为什么呢？

生1：可能两盘桃的个数不一样。

生2：可能孙悟空的那盘桃很多，猪八戒的那盘桃却很少。

（很多学生表示赞同）

师：很有想法。你能用小圆圈来表示桃，用虚线分一分，找到这盘桃的1/2吗？

（学生活动，很快有人举手）

生3（上台展示自己的分法）：我用10个圆圈表示孙悟空的那盘桃，它的1/2有5个；用2个圆圈表示猪八戒的那盘桃，它的1/2只有1个。猪八戒的太少了，所以他才会哭。

生4：我用8个圆圈表示孙悟空的那盘桃，它的1/2有4个；用4个圆圈表示猪八戒的那盘桃，它的1/2有2个。

师（指着其中的一盘桃）：能说说你是怎样找到这盘桃的1/2的吗？

生5：只要把8个桃平均分成两份，其中的一份就是1/2。

师（指着另一盘桃）：为什么从4个桃里也能找到1/2？

生6：因为把4个桃平均分成两份，其中的一份就是1/2。

生7：不管盘子里有几个桃，只要平均分成两份，就能找到它的1/2。

生8：无论桃有多少，找到了一半就能找到1/2。

师：很有见解！我们可以把一盘桃看作一个整体（画圈），平均分成两份，每份就是它的1/2。

上述教学中，学生在无法清晰表达“两盘桃到底有何不同？”时，教师创设了生动有趣的“分桃子”的情境，借助“画一画”“分一分”“比一比”等活动，引导学生展开生生对话、自我对话，而教师恰当的追问、反问，能引领学生逐步触及知识的本质——“部分与整体的关系”，加深对“分数具有无量纲性”这一本质的理解。

二、多维互动，让学生自主探究

曹培英老师认为：学科核心素养不是针对学科专业人才的特殊需要，而是适用于普遍情景和所有人的共同素养。课堂学习的多维互动有利于学生思维品质的拓展和提升，而对于不同的学习素材和数学问题，不同的学生也会有不同的理解，这为课堂开展对话教学奠定了基础和提供了契机，也为学生核心素养的培养提供了生长的“土壤”。

例如，在教学“认识小数”时，教师组织学生进行如下实验探究。

师（出示图2）：下面的每个图形都表示1角，你能在图中表示出0.1角吗？在学习单上试一试。

图2

（学生独立思考，自主完成）

生1（上台展示）：我选择的是线段，在左边画一段，就是0.1角。

生2：不准确。随便画一段，不一定是0.1角，应该把线段平均分成10份，其中的1份才是0.1角。

师：很严谨，画图就应该准确。还有不同的想法吗？生3：我把长方形平均分成10份，其中的1份是0.1角。生4：把正方形平均分成10份，其中的1份也是0.1角。师：为什么一定要平均分成10份呢？

生4：1角等于10分，平均分成10份，1份就是1分，也就是0.1角。

师：这种平均分的方法，还可能得到什么数呢？生5：1/10。

上述教学中，充分利用学生已有的认知经验，引导学生根据“分一分”“涂一涂”直观图来研究小数的意义，适时展开师生、生生对话，可使“小数”从具体的量中抽象出来，从而使数学建模的过程更具深度，也为学生初步理解“小数实质上是十进分数的另一种形式”提供经验支持，能让学生真正体验到小数的产生是生活和生产的需要。给学生提供丰富的数学活动材料，引导学生经历探索的过程，不但能为学生创设合理想象、自由思维的空间，把学生带到从未知走向已知的“高速”通道，还能使知识在教学层面实现“软着陆”，往往会有“意外”的收获。

三、因势利导，让学生主动思辨

对话是课堂建设者之间一种共生的交往关系，意味着对话主体间的相互理解、视界融合及经验分享。引导学生主动思辨，经历核心知识的形成过程，并且让学生正确理解核心知识，学会“用数学的语言表达世界”，就有可能让学生逐步养成数学的理性思维。

例如，教学“表面积的变化”时，教师设疑并组织学生讨论。

师（出示图3）：如果从棱长为3 cm的正方体上挖去一个棱长为1 cm的小正体，它的表面积会发生变化？

生1（很快举手）：挖去一部分，大正方体的表面积当然会变化。

师：你能说说它的表面积是怎么变化的吗？

生1（迟疑）：应该会变小吧。

生2（很快反驳）：不一定会变小，也有可能不变。

师：你能具体说一说吗？

生2：如果从顶点处挖，大正方体的表面积应该是不变的。

师：对于这个问题，你们还有什么新的想法？

（学生猜想、操作、验证结论）

生3：从一个顶点处挖去3个小面，但又露出了3个小面，大正方体的表面积确实不变。

生4：从一条棱的两边各挖去1个小面，但又露出4个小面，大正方体的表面积反而增加了。

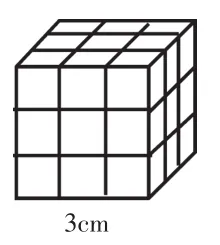
图3

生5：从一个面的中间挖去1个小面，但露出了5个小面，大正方体的表面积增加了4个小面。

师：采取的方法不同，大正方体的表面积的变化也不同。

以核心问题为载体、学生自主参与为主线的学习活动，更需要适时展开师生、生生对话。一方面，可以促使学生深入了解学习素材，从整体上建立对数学知识的初步感知；另一方面，还能指向学生的最近发展区，优化学生的思考方式，引发学生新的思考和感悟，实现深度学习。

四、长效提升，让学生合作共赢

数学课堂的教学设计要有“教育的格局”，不囿于一题、一课，而应着眼于学生的生命成长，体现知识、能力、情感培养的整体性。课堂不能流于单一的“问答式”，而应通过交流、争辩、质疑、分享等方式，实现教学主体之间的多维度对话，从而建构一个以知识、能力、人格为基础，以数学素养、生命成长为顶层的学习空间。

例如，教学“用数对确定位置”的结课阶段，教师组织学生讨论。

师：刚才我们学习了用数对确定位置。那么你觉得确定一个点的位置，需要几个数呢？

生1：2个数。

师：如果只用一个数，行吗？

生1：肯定不行。

师：为什么？（出示图4）谁能说说在0和2中间的这个点可以怎样表示？

图4

生2：可以用“1”表示。

师：你看，刚才的这个点，不就是只用了一个数就确定位置了吗？那么，“3”的位置在哪呢？

生3：在2的后边。

师（笑）：还是只用一个数就确定了它的位置。

生3（反应过来）：情况不一样。这里只有一行，确定点的位置，当然只需要一个数了。

生4：今天学的不只是一行或一列，而是好几行好几列。需要先确定它在第几列，再确定它在第几行，所以要用到两个数。

师：真会思考！这样看来，确定位置有可能用一个数，有可能用两个数，那么——

生5：还有可能用到三个数。

师：确定位置时，究竟会不会用到三个数呢？这个有趣的问题，留给同学们课后研究。

综上，对话为学生创设了“伸出窗外”的空间，为学生的数学思维走向更深层次提供了无限可能。实施多样的对话，引领数学学习从经验走向理性，让学生真正“学得到”“带得走”，是数学生态课堂发展的必然诉求，是对发展核心素养的积极回应。