直立型石笼护岸结构应力变形及岸坡稳定性影响因素分析

许长云

(江西省赣州市天鹰勘测设计有限公司，江西 赣州 341000)

0 引 言

现代城市河流的治理除防洪外就是沿堤岸形成园林化景观以及河流的水质环保问题。因此，合理科学地建设城市堤防工程对保护河岸生态、控制生态破坏是十分必要的[1-3]。

生态型护岸型式能够增进河岸与河水的渗透性能，创造良好的生物生存环境，进而促进河道生物的多样性，加强河水的自净能力，同时也可创造出美丽的天然景观[4-6]。

本文采用有限元数值模拟软件，建立了石笼挡土结构的数值模型，考虑了3种填土压实度、石笼高度、基础延伸长度等因素，对石笼护岸结构进行了应力变形分析及岸坡稳定性分析，并对各因素进行了敏感性分析。

1 生态型石笼挡土结构特点

石笼护岸结构，也称格宾结构，早在古代就出现过，古人采用藤条编成的竹笼框里面填筑石块，用于封堵河道缺口，比如在都江堰修建时，石笼结构被大量运用于水利工程的建设中[7-9]。

在国内，石笼结构用于河道护岸结构的工程较多，大体上可以分为重力式挡墙结构和加筋土挡墙结构，其中重力式挡墙结构又分为直背型和阶梯型。如图1所示，石笼结构是由六边形钢线组成的方形笼子，具有六角形的网孔，内部填筑块石，块石适用当地山体石料。按高度分类，石笼网箱有三种型号，即1.0 m、0.5 m和0.4 m。

图1 石笼及石笼挡土结构断面示意图

2 石笼护岸结构有限元模型建立

2.1 有限元几何程序的确定

MIDAS-GTS是一款针对岩土领域研发的通用有限元分析软件，不仅支持线性/非线性静力分析、线性/非线性动态分析、渗流和固结分析、边坡稳定分析、施工阶段分析等多种分析类型，而且可以进行渗流-应力耦合、应力-边坡耦合、渗流-边坡耦合、非线性动力分析-边坡耦合分析。广泛运用于地铁隧道、边坡、基坑、桩基、水利工程、矿山工程等各种工程的建模分析。本文采用此软件对石笼挡土结构进行应力变形、边坡稳定性分析。

2.2 石笼护岸结构的几何模型

采用有限元数值计算软件，针对直立式的石笼挡土结构进行建模，同时考虑了石笼高度(7.0 m、6.0 m、5.0 m)、基础延伸长度(0 m、1.0 m、2.0 m)。每层石笼高度为1.0 m，具体结构尺寸和材料详见模型几何简图如图2。

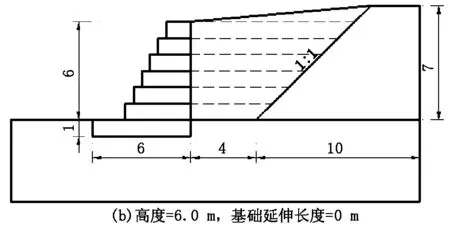
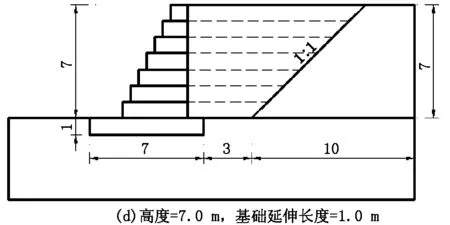
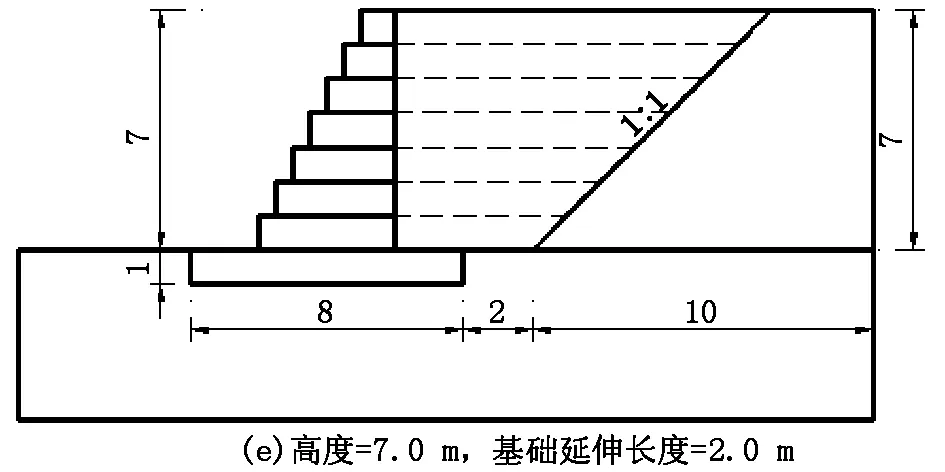
图2 直立型石笼挡土结构计算工况简图

2.3 计算假定及材料参数

为了探讨石笼挡土结构在施工过程中岸坡的力学响应以及岸坡的稳定性，采用了有限元数值计算软件进行分析。

虽然在实际工程中石笼网结构由石笼和块石填料所组成，但工程中关注的是石笼挡土结构整体稳定性以及其对岸坡的固坡效应，因此，在数值模拟之前，提出以下假定：①假设石笼网与块石填料之间无相互滑移，将两者视为整体进行考虑，材料采用理想弹塑性本构模型，屈服准则采用Mohr-Coulomb准则；②将石笼块石填料考虑成连续介质。

计算所采用的材料力学参数根据文献[10]进行取值，如表1所示。

表1 计算材料参数

在有限元计算分析中，根据以下步骤进行操作：①建立几何模型；②对材料进行分区，设置材料参数；③划分有限元网格；④对模型施加重力和模型边界条件，其中模型两侧施加水平约束，底部施加固定约束；⑤对原始地基进行初始地应力分析；⑥对基础进行换填；⑦分层施工石笼、填土，先施工石笼结构，然后再填土，逐步施工至结束；⑧回填土体上部加工作荷载。⑨执行计算，并分析。

2.4 计算工况

针对石笼挡土护岸结构进行数值模拟，主要分析其在施工过程中的应力变形情况以及不同因素对护岸结构稳定性的影响。

工况1～3探讨填料压实度的影响，工况3～5探讨石笼结构高度的影响，工况3、6、7探讨石笼结构基础换填延伸长度的影响。

为方便计算，本文将填筑顺序进行以下处理。以工况1为例，当基础换填后，本文其分层填筑过程如下：①石笼第1～2层填筑；②填筑第1～2层回填土；③石笼第3～4层填筑；④填筑第3～4层回填土；⑤石笼第5层填筑；⑥填筑第5层回填土；⑦石笼第6层填筑；⑧填筑第6层回填土；⑨石笼第7层填筑；⑩填筑第7层回填土。

模型网格划分图如图3所示。

表2 计算工况

图3 模型网格划分图

为监测施工过程中结构的应力、变形数据，计算点设置如图4所示，其中1～7点为监测施工过程中的变形情况，A点为监测水平、竖向应力情况。

图4 计算点示意图

3 施工过程应力变形分析

3.1 不同填土压实度

通过提取工况1～7的模型中计算点1～7和A点的计算结果数据，得到石笼挡墙墙背底部测点A的水平土压力变化趋势以及石笼挡墙前端变形数据。

从图5可以看出，随着填筑过程的进行，测点A的水平土压力逐渐增大，每次填筑回填土后，土压力有一定幅度的增加，从增长规律来看，每层施工引起的土压力增长比较均匀(第2步和第4步填筑了2层)。通过对比，发现回填土压实度越高，墙背底部测点A的水平土压力越小，说明提高回填土的压实度有利于石笼结构的受力。

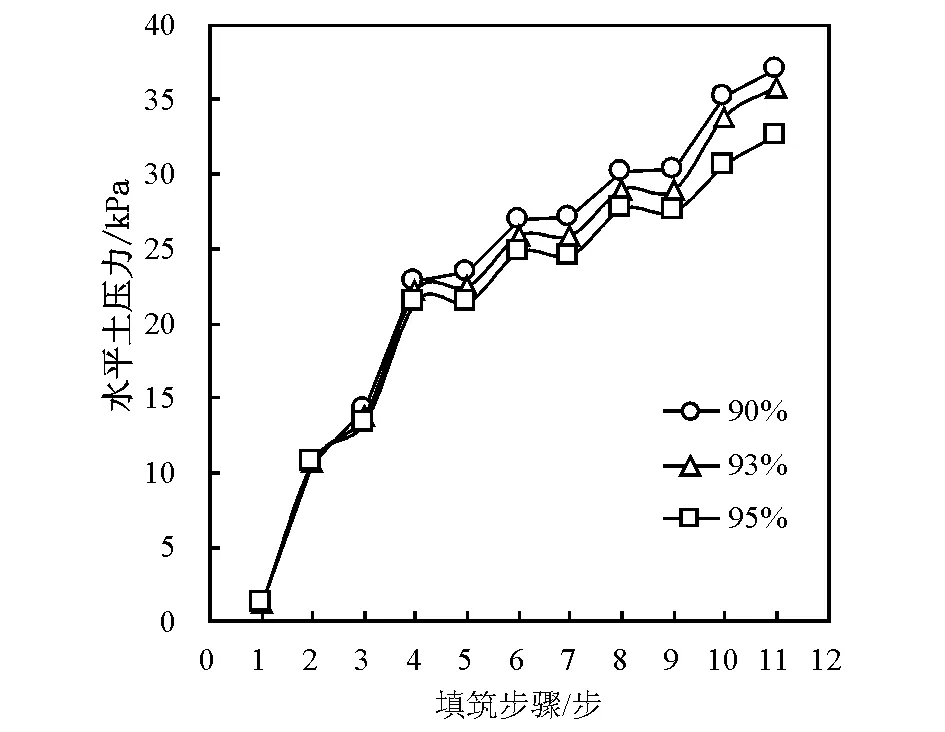
图5 施工过程中石笼挡土结构A点水平土压力变化趋势(不同填土压实度)

图6 施工结束后石笼挡土结构水平位移变化趋势(不同填土压实度)

图6为施工结束后不同填土压实度情况下石笼挡土结构墙背水平位移变化趋势。从水平位移规律分布情况来看，最大位移点并不处于石笼结构的两端部，而是出现在石笼挡土结构的中部。由此说明，在回填土和顶部荷载引起的侧向土压力作用下，石笼挡土结构有向外侧倾斜的趋势，其最大变形点处于墙中部，即向外鼓出。从数值大小来看，填土压实度增大，石笼挡墙中下部的变形略有减小。

3.2 不同石笼高度

图7为不同石笼高度对墙背底部测点A的水平土压力的影响。从图中发现，石笼高度越小，测点A的水平土压力增长速度越快，施工结束后，三种工况下测点A的水平土压力基本一致。

图7 施工过程中石笼挡土结构A点水平土压力变化趋势(不同石笼高度)

从图8发现，对于石笼挡墙下部，石笼高度越大，其水平位移越小；对于石笼挡墙上部，石笼高度越大，其水平位移越大。在墙高4.0 m处，鼓胀变形达到最大，且石笼高度为7.0 m时其水平位移越小。

图8 施工结束后石笼挡土结构水平位移变化趋势(不同石笼高度)

3.3 不同延伸长度

为探讨不同基础延伸长度对石笼挡土结构应力变形的影响，给出图9。对比发现，基础延伸至2.0 m后，墙背底部测点A的水平土压力较基础未延伸时增加了10 kPa左右，延伸1.0 m和延伸2.0 m增加的土压力基本一致。

图9 施工过程中石笼挡土结构A点水平土压力变化趋势(不同延伸长度)

从图10可说明，基础延伸后，石笼挡土结构中部的鼓胀变形得到了减小，而顶部变形发生增大。随着延伸长度的增加，中部变形逐步减小，不过延伸1.0 m和延伸2.0 m效果基本一致，因此在本模型，为提供石笼挡墙的稳定性，基础延伸至1.0 m即可。

图10 施工结束后石笼挡土结构水平位移变化趋势(不同延伸长度)

4 挡土结构对岸坡稳定性影响

采用有限元强度折减法对各方案的岸坡模型进行稳定性分析，计算结果如表3。

表3 不同计算工况下岸坡稳定性计算结果

从表3发现，回填土上方加荷后的稳定性系数较填筑结束时的稳定性系数略有下降，降幅在6.25%～8.06%之间。为进行因素敏感性分析，对数据进行整理并作图，分析结果如下。

4.1 不同填土压实度

从图11可知，对于石笼挡土结构，当回填土压实度为90%、93%、95%时，岸坡稳定性系数分别为2.73、2.80、3.05，总增幅为11.72%，说明提高回填土压实度对岸坡的稳定性是有利的。

图11 不同填土压实度对石笼岸坡稳定性系数的影响

4.2 不同石笼高度

从图12可知，当石笼高度为5.0 m、6.0 m、7.0 m时，岸坡的稳定性系数分别为3.78、3.36、3.05，总降幅为19.31%。

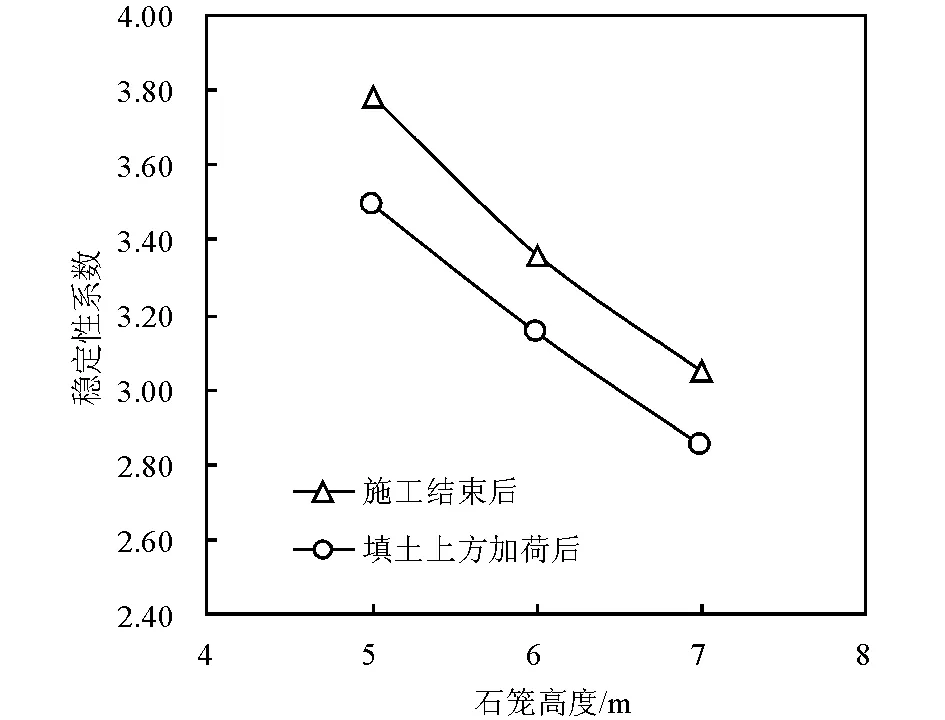
图12 不同石笼高度对石笼岸坡稳定性系数的影响

显然，岸坡越高，稳定性系数越小，在实际施工时，应合理控制石笼挡土结构的高度。

4.3 不同基础延伸长度

图13 不同基础延伸长度对石笼岸坡稳定性系数的影响

从图13中可得到，基础延伸长度对岸坡的稳定性影响几乎可忽略不计，分析其原因，主要是因为本文建立的岸坡模型中最危险滑弧并不是深层滑动形式，此外，原地基土体强度参数并未远小于石笼的参数，因此基础延伸长度的加大对岸坡整体稳定性的影响并不是很明显，其目的主要是为了增强地基承载能力。

4.4 典型滑弧分析

以工况3中石笼高度为7.0 m、基础延伸长度0 m、压实度95%为例，采用强度折减法对施工结束后的岸坡进行稳定性分析，得到岸坡的位移矢量图及最大剪应变云图，见图14和图15。

图14 工况3岸坡位移矢量图(强度折减法)

图15 工况3岸坡塑性应变云图(强度折减系数=3.05)

从图14可看出该岸坡有失稳滑动的变形趋势，图中黑色的曲线为大变形区域与小变形区域的分界线，与图15中的最大剪应变区域一致，可代表该岸坡的最危险滑弧，均通过了第二层石笼填筑体(石笼高度2.0 m处)。

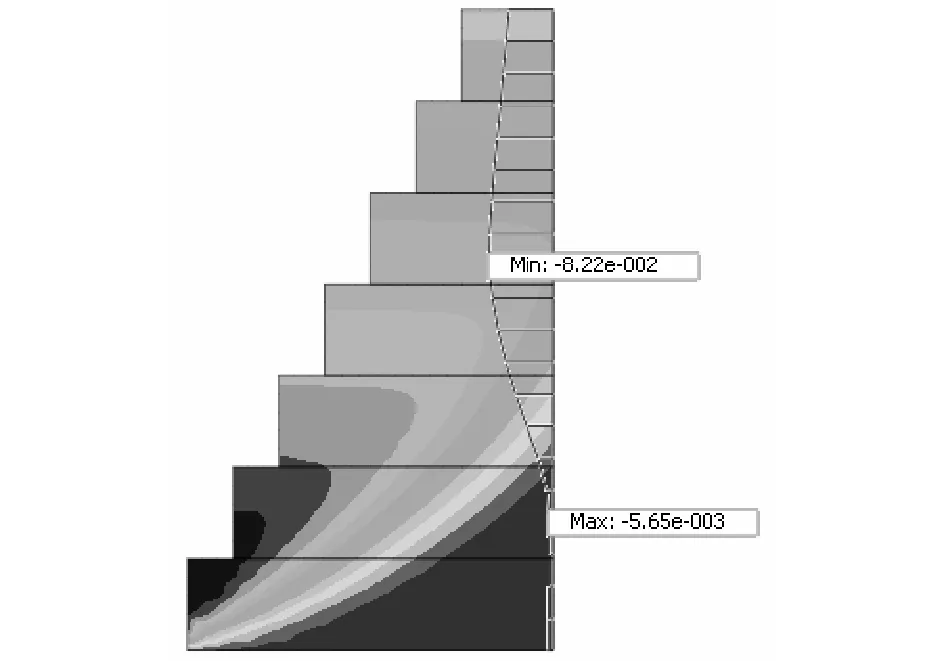
图16 工况3石笼结构变形云图(强度折减法)

单独观察石笼结构的变形，从图16可发现，在第四层石笼填筑层(石笼高度为4.0 m处)，水平位移发生最大，与第3节描述相符合。

5 结 论

本文针对直立式石笼护岸结构，采用有限元数值模拟手段，考虑回填土压实度、石笼高度、基础延伸长度，对石笼挡土结构的应力变形及岸坡的稳定性进行敏感性分析。

结果表明，提高回填土的压实度，有利于减小石笼挡墙的变形，同时有利于提高岸坡整体的稳定性；石笼挡墙高度越低，其自身稳定性及岸坡稳定性越高；基础延伸长度有利于石笼挡墙的稳定性，因此在工程中对基础延伸长度适当控制即可。此外，在本文模型的几何结构和材料参数的条件下，岸坡最危险滑裂面并不是深层滑动，因此增加基础延伸长度对岸坡整体稳定性基本无影响。