基于MDID模型测评ITS改善城市交通拥堵的贡献
2018-09-05
(信阳师范学院 旅游学院, 河南 信阳 464000)
一、引言
2011年,国家启动了“国家物联网应用示范工程”,在交通、农业、公安、林业等八个领域开展典型示范应用。其中,交通运输部结合行业发展现状,着眼于物联网产业的推动发展,以广州为示范区域,组织开展了“基于物联网的城市智能交通应用示范工程”。为此,交通运输部设立了“基于物联网的城市智能交通关键技术研究”重大信息化科技专项。智能交通系统(Intelligence Transportation System,以下简称ITS)作为物联网技术在交通行业应用的新生产物,与传统交通运输项目相比,它表现出动态性、新颖性、复杂性、广泛性等特点。目前,ITS已经在中国开始建设并应用,在改善城市交通运行与服务的畅通性、安全性、绿色性、便捷性等方面已经取得了一定的成效。
城市智能交通是一个复杂的综合性系统,其发展建设受城市交通环境、人口、地理位置、经济水平等众多因素影响。尽管智能交通产业建设在多个领域已经取得了显著效果,交通运输整体状况也得到一定程度改善,但是,关于ITS应用效果的研究仍然以宏观层面的管理、建设为主导,对ITS微观层面应用效果的研究较为匮乏,比如,ITS对城市交通出行环境,出行服务质量,出行的畅通性、安全性等改善的研究成果很少。从已有成果来看,ITS应用绩效评价研究多从其产生的经济效益、社会效益等宏观输出层面入手分析,比如,美国2000年发布的“National ITS Architecture”对ITS的评价内容做了较全面阐述,包括评价设计、成本分析、性能效益研究、风险分析、评价指导性文件。此前,美国运输部还公布了其他有关APTS(Benefits Assessment of Advanced Public Transportation System)评价的指导性文件,如“1994年ITS评价指导方针TEA-21中的AVIS评价指南”。日本在ITS经济效益评价的基础上,针对不同ITS子项目设计了相应的评价方法,重点考察ITS的社会效益。欧盟则在“1994-1998 TELEMATICS计划”中指出,ITS评价的主要方向为:为公众提供出行信息、路线引导和事故报告服务,为车辆提供自动定位、最佳路线选择和信息交换服务,为公共交通提供准确的信息和乘车服务,为交通管理提供自适应交通信号、自动收费、环境监测和事故自动检测服务等。除了国家宏观发展层面提出的评价措施,学者们也进行了研究,史其信、梁玉庆、陆化普、高自友、黄海军等较早评价了ITS的应用效益,并初步将评价指标概括为:降低交通成本、减少出行时间、缓解土地资源及交通基础设施投资强度、推动相关产业发展和技术进步、满足交通需求和提供高生活质量以及其他社会经济效益〔1~5〕。之后,评价指标开始被分类细化,比如从公共交通设施水平、服务水平、效益水平、社会责任四个层面建立综合评价指标体系〔6~8〕;以舒适、安全、便捷、时效等为指标,从定性与定量相结合的层面评价快速公交换乘系统的应用效益〔9~12〕,并准确提出了评价ITS综合效益的指标体系〔13〕。此外,有学者从宏观应用层面按照社会效益、个人效益、企业效益等对ITS进行评价〔14~16〕;从ITS建设投资层面,探讨了ITS对直接就业人数、经济乘数、生产率、技术扩散和竞争力等潜在宏观经济的影响〔17~18〕;但是,由于很多地区的ITS核心基础设施并未广泛建成,导致指标度量较为困难。Brand,Levidkangas等对ITS项目自身的效益进行评价,实现对不同ITS子项目的筛选、排序和选择〔19~20〕。综上可知,已有研究成果从不同视角构建了不同指标体系,结合了不同方法对ITS的应用绩效进行了评价;但是,综合分析之后发现,存在以下问题:第一,由于评价对象受到的影响因素较多且具有一定交叉性,使得评价方法选取受限,导致定性或模糊数学等主观性较强的方法成为了主导方法,影响了结果的准确性;第二,大部分评价研究停留在宏观层面,对微观层面的定量化评价相对匮乏。因此,本文尝试进行改进和创新,在考虑“投入—产出”的前提下,通过构建立体式、动态性的评价指标体系,评价ITS对城市交通拥堵改善的贡献。
二、模型的构建
虽然笔者在前期研究ITS的应用时,借助DID模型评价了ITS对交通拥堵改善的作用;但是,DID模型在测算贡献率时,主要针对那些在短期内有较大变化且容易选取对照组的领域,而对于交通等一些较复杂领域的研究涉及较少,对ITS应用效果以及对城市交通拥堵改善贡献的研究也相对空白。此时,DID模型的使用受到限制,而ITS的复杂性决定了选取对照组时的困难。因此,探寻一个有效选取对照组的方法,能较好的使用DID方法评价ITS的应用效果。本文主要通过引入匹配算法,构建匹配双重差分模型(MDID)来解决这一问题。
(一)模型应用思路
DID模型应用的核心思想是:以建设了ITS的地区为“实验组”,未建设ITS的地区为“控制组”,利用DID模型有效控制其他可能因素的影响后,既能分离出实验组在ITS应用后交通运行状况变化的个体差异,又能分离出不同区域在时间上的差异,从而识别出ITS的应用效果(图1)。
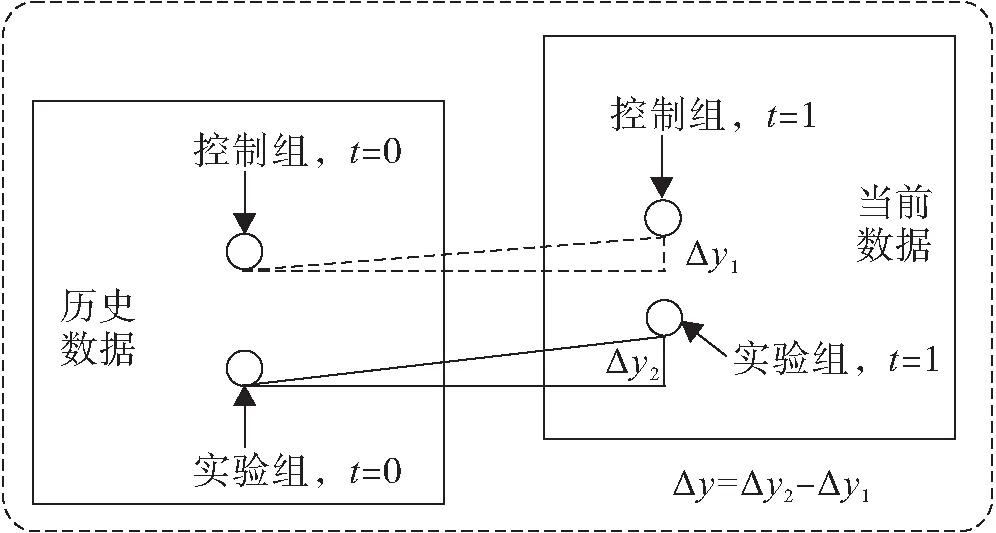
图1 DID模型评价ITS应用效果时的框架
从DID模型的研究和应用现状来看,控制组的选取主要依靠主观判断,缺乏客观定量的衡量标准;当控制组为单一个体时,计算结果会严重依赖于该个体的数据,造成模型稳健性不高,因此,需要对模型进行改进。同时DID模型在选取控制组时主观性太强,影响了ITS应用效果评价结论的真实性,可引入匹配算法加以解决。匹配算法并非真正意义上的实验算法,是通过采用一种近似实验的算法处理一些难以有效区分实验组和控制组的数据。匹配算法认为具有相同特征的个体对同一政策变量有相同的反应,即在ITS应用效果评价的过程中,实验组和控制组的决策行为不受不可观测变量的影响。将匹配算法引入DID模型之后,扩大了控制组的选择范围,避免了控制组选取的主观随意性,消除非共同支撑域和非同分布所导致的估计偏差。
(二)MDID模型构建
MDID模型是在DID模型基础上引入匹配模块,使用匹配算法寻找最优控制组,然后通过构建干预实施前的虚拟处理个体,在匹配选取的控制组基础上进行双重差分。MDID模型在测算贡献率时具有以下优点:(1)解决了DID模型选取控制组时的人为因素;(2)匹配算法无法解决不可观测的时间固定效应,而DID模型可以解决;(3)MDID允许存在不可观测因素的影响;(4)在实施拟合过程中,国内城市的车速数据较难获得,而MDID模型的匹配过程不需要大量的车速数据,使构建较大备选库成为可能,减少了控制组选取时的人为因素;(5)MDID模型的理论相对完备,便于进行检验和推断。
1.DID模型
一般化的DID估计模型为yi=β+αidi+ui。其中,虚拟变量di=1表示实验组对象,di=0表示控制组对象。实验组的平均处置效应(Average treatment effect on the treated,ATT)度量处理组和控制组的平均回报,为考察动态变化,引入时间变量的估计模型为:
yit=β+αidij+uij。
其中,虚拟变量t=t0表示政策实施前的时间区段,t=t1表示政策实施后的时间区段,且政策实施仅对实验组有影响(外生性假定),由此可得ATT为,
The magnitudes of the grain size D, dislocation density δ, and the strain ε of the CuInGeSe4 thin film are found to be 48 nm, 3.93 × 10−3, and 1.14 × 1012 line/cm2, respectively.
αATT=E[α|di=1]
={E[yit|di=1,t=t1]-E[yij|di=1,t=t0]}-{E[yit|di=0,t=t1]-E[yit|di=0,t=t0]},
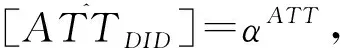
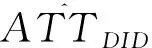
2.匹配算法
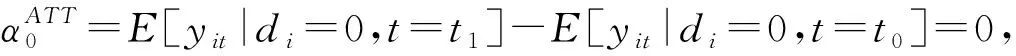
Pr(D=1|Y(0),Y(1),PS(X))=Pr(D=1|PS(X))=PS(X),
在处理PS时,选择Probit模型进行回归分析,通过以下公式得到匹配估计值:
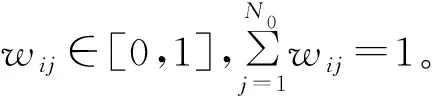
根据双重差分和匹配估计量,建立匹配双重差分估计量:
考虑到包含其他影响因素的控制变量,可以构造如下面板模型估计ATT的取值:
wijyit=β0+β1tit+β2xit+αidit+γtitdit+δi+μit。
yit为随机变量,wij为权重,xit为控制变量,β0、β1、β2为系数向量,参数β1表示没有政策干预时实验组与控制组的经济行为如何随时间变动,δi,uit为随机干扰项,不随时间变动。αi为实验组和控制组中任何不随时间变动的差异,titdit是虚拟变量交叉项,γ表示实验组接受政策后的变动程度,反映了政策变动的效应,是目标变量,不仅度量了政策实施前后的效果,也度量了实验组与控制组之间的政策差异。
三、ITS对交通拥堵改善的贡献
(一)指标分析
笔者在前期研究成果中指出:交通拥堵可从畅通状态和效率两个方面来解释,而城市交通运行的畅通性取决于路网中各个路段或交叉口处的交通状况。一般来讲,导致城市交通拥堵的原因有很多,归根结底是交通需求与交通供给的不匹配、不协调。交通需求方面,主要受城市经济、交通构成、机动化出行等因素的影响;交通供给方面,包含了城市交通管理与规划、道路基础设施及相关交通服务设施等〔21~22〕。基于以上分析,挑选可量化且数据可获取的因素形成指标集(见表1),并进行分析。
根据前文分析,本文选择路网平均行车速度(A-SPEED)作为交通拥堵的表征指标,考虑指标之间的规律性和数据可获取性,定量分析并明确指标间的相关性。主要以北京市为例,收集北京市2000~2010年的指标数据,并利用Eviews软件进行相关性检验,结果如表2所示。

表1 影响交通拥堵的主要指标

表2 交通拥堵表征指标与路网平均行车速度之间的相关性
结果显示,GDP、POP等影响因素与A-SPEED之间的相关系数均在0.7以上,相关性较高,是影响A-SPEED的主要因素。参考国内外学者已研究的交通拥堵评价指标的基础上,根据“从一般到简单”的计量建模原则,对指标进行筛选。MDID模型中的CIA假设为自变量的筛选提供部分依据:自变量被“干预”所影响,但不能影响“干预”。根据MDID假设条件,实施格兰杰检验,剔除不满足CIA条件的变量。检验结果表明,P-POP为车速的格兰杰原因的检验结果是显著的(P<0.05),说明P-POP不适宜作为A-SPEED的自变量。
(二)构建匹配池
双重差分方法需要控制组城市,广州作为ITS示范工程的唯一城市,作为控制组的对比城市是未实施ITS的城市,但手工选取对比城市存在两个缺陷:一是作为广州的对比城市可以容忍多大的差异,是10%还是30%,没有客观的标准;二是如果选择单一城市,计算结果会严重依赖于这一城市的数据。通过引入匹配过程可解决以上两个问题,为科学选取最优对比城市提供了理论支持。但执行匹配算法之前,需要确定哪些城市可进入匹配池。根据模型原理,选取控制组城市时假设政策具有外生性,即政策不应与误差项相关,ITS仅影响广州而对控制组城市没有影响或影响以忽略。此假设引申的要求为:(1)模型允许存在不可观测因素的影响;(2)除政策外,其余因素的影响作用相同;(3)控制组和实验组的特征稳定。根据以上要求,结合中国行政区划,选择30个省会中心城市(拉萨除外)和大连、深圳、厦门、青岛、苏州、宁波6个城市组成匹配池,并采集36个城市2015年的数据作为备选库截面数据。对原始数据进行Probit稳健回归,结果如表3所示。
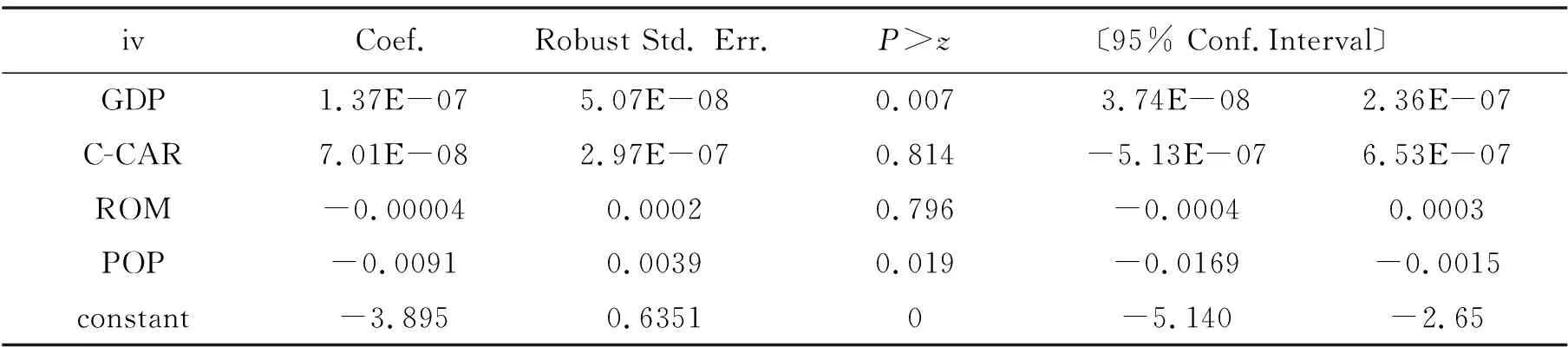
表3 交通拥堵表征指标的Probit稳健回归结果
由表3可知,P-BUS在Probit回归中,系数稳健检验不显著,且与C-CAR存在较高的共线性,但它与A-SPEED的相关度低于C-CAR的相关度,因此不适于进入模型。将其剔除后,R2,AIC/SIC变化并不明显。此外,ROM和ROA存在不容忽略的共线性问题,不适于放在同一模型中,保留ROM之后,4个自由度的Wald统计量为19.89,P值为0.0005,Log pseudo似然度为-2.276,PseudoR2为0.782,拟合程度可以接受。
Probit回归后,在共同支撑域下计算PS值。采用半径法匹配算法(半径取值为0.1%)选取控制组城市并计算权重。结果显示,控制组组城市为深圳、上海和苏州,并采用Gaussian核密度函数进行计算,高斯宽度参数设为0.1,计算结果见表4。
为保证模型的稳健性,对数据进行对数化处理,重新计算得到的PS值为:0.226(广州),0.405(深圳),0.170(上海),0.137(苏州),说明模型具备较好的稳定性。因此,可虚拟一个城市A为控制组,即城市A=0.403×深圳+0.139×上海+0.458×苏州。
(三)贡献率测算
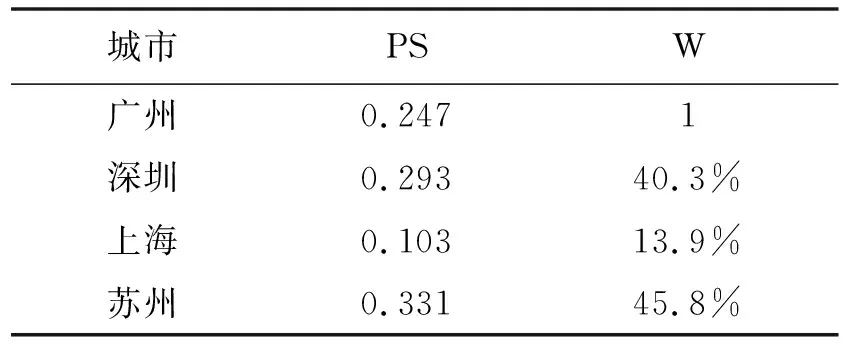
表4 PS值和权重
其余32个城市,PS值均小于0.001。不再罗列。
根据上述内容,采集实验组和控制组城市2008~2015年的指标数据,为了与被解释变量A-SPEED保持一致,分别对变量除以常住人口,得到人均变量。假设,贡献率为因x变动引起的y变动除以总的y变动,比照索洛增长模型,取对数差分后,虚拟变量系数即为贡献率。设组别虚拟变量为GRP,GRP=0表示变量隶属于控制组,GRP=1表示变量隶属于实验组,ITS为政策虚拟变量,交叉项为GRP×ITS,可建立最终的贡献率测评模型:
W×A-SPEED=a0+a1×ROM+a2×C-CAR+a3×GDP+b1×GRP+b2×ITS+b3×GRP×ITS+μ。
由于上述数据是非对称分布的,条件期望的最小二乘模型难以精确反映真实情况,因此,本文建立了以下固定效应估计模型,使用分位数回归模型进行拟合,对模型的稳健性进行检验,计算结果为表5。
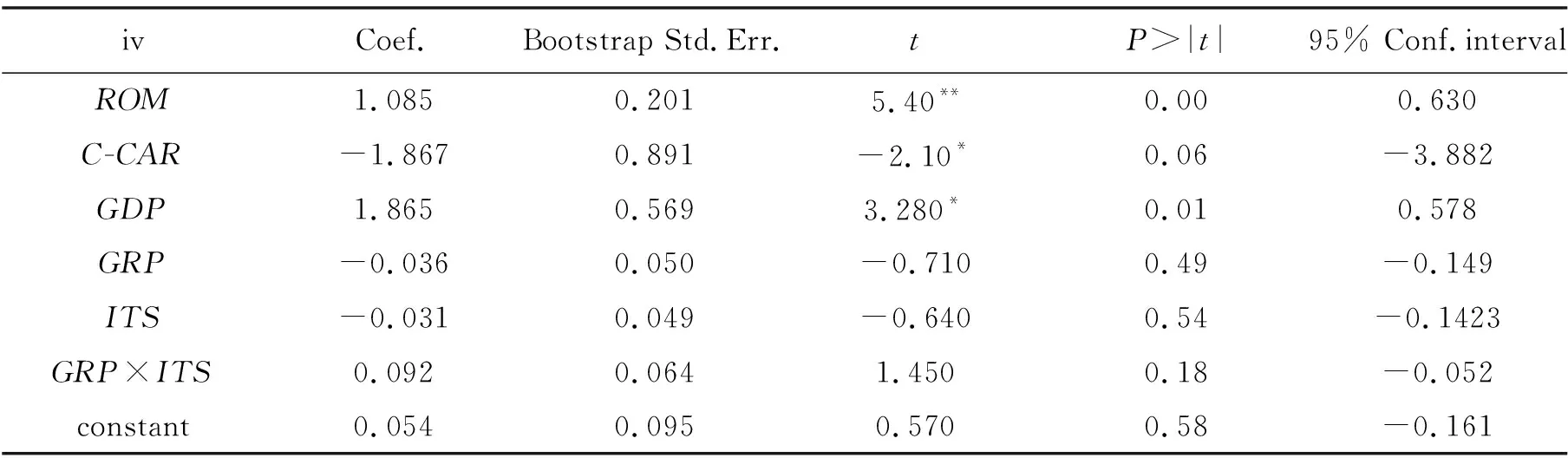
表5 匹配双重差分模型估计结果
由表5的测算结果得出以下结论:
(1)实施智能交通项目对广州路网平均车速提高的净贡献为9.25%,即在广州交通堵改善的提升中,有9.25%是由ITS项目贡献的。
(2)由方差R2=0.704可知,包含4个变量和2个自由虚拟变量的模型解释了总变动的70.41%,其余约30%的变动是模型未包含的因素造成的,包括系统性误差、遗漏变量、变量约简误差、其他无法解释的误差等。
(3)截距系数constant=0.054。由于控制组不可能完全没有建设ITS,因此,该值表示控制组城市受ITS影响的比例为5.4%,比值较小,可忽略,说明控制组的选取是科学合理的,也佐证了贡献率测算结果的真实性。
(4)政策虚拟变量系数值为-0.031,表示受时间因素及其他因素影响,从2008~2015年,控制组城市交通畅通性水平减少了3.14%,该值较小,说明控制组交通畅通性在该时间段内较为平稳,有益于使用MDID模型进行贡献率测评。
(5)GRP的系数为-0.036,表明在ITS实施前,控制组与处理组之间的交通畅通性水平差异较小,仅为3.6%,说明控制组与处理组选择的较为合理。
(6)ROM、C-CAR和GDP的系数分别为1.085、-1.867和1.865,说明道路长度和GDP与畅通性存在正相关关系,且GDP的相关性高于道路长度;而民用机动车拥有量与畅通性存在负相关关系,且对畅通性的影响较大。
(四)测算结果分析
ITS的应用必然会给城市交通发展带来积极影响,但是伴随城市自身的快速发展,加之ITS受较多因素的作用,城市交通拥堵并没有得到明显改善。因此,基于以上结论,本文从以下几个角度提出改善城市交通拥堵的策略建议。
(1)提升城市交通管理水平,改善现有路网结构。城市要能够认准市场经济体制的要求,参考城市交通的自身发展现状,推进管理体制的改革,如积极推行政企分开、政事分开,优先发展公共交通,加强信息化技术的使用,发展多核心城市空间结构等;在进行路网规划时,要在对未来很长一段时间交通环境预测的基础上进行预见性的规划,避免出现后期建设否定前期成果的情形;完善静态交通设施,如建立立体化车库。
(2)保证城市发展进程下有效改善交通拥堵。城市经济发展、人口增多势必会增加机动车的保有量,从而影响交通畅通状态,而此时可采取提高车辆税、停车费、收取道路拥挤费及公共交通出行优惠等手段,利用价格机制合理引导交通需求,缓解拥堵。如提高停车费、收取道路拥挤费及实施公共交通出行优惠等手段可限制城市外围车辆进入城市中心区域,鼓励换乘公共交通工具。
(3)优化城市交通基础运行状况。目前,我国机动车保有量以每年15%的速度增长,而城市道路仅以3%的速度增长,这种比例极不合理,由于城市土地资源是有限的,需要我们最大效用利用有限的土地资源。因此,可采用多种方式改善道路使用程度,如建立互通交叉立交桥、采用环岛行交叉路口、交通灯智能化控制路口等改善路网行车速度;合理设置不同等级道路的交叉口间距、加强道路之间的互通互联率、缩短出行距离,安装智能化路况显示屏、合理分配交通流量、减少出行时间;强化城市快速路和城市支路建设、合理控制道路两侧的预留用地等。
(4)合理配置交通构成方式。加强公交设施和服务的改进,吸引更多人群出行改用公交车,如优化公交布局、发展多种形式的快速公交专车、实行峰谷时段收费不同的优惠公交卡等,提高公共交通分担率。
四、总结
本文研究结论为城市ITS的规划及建设投入提供了定量分析方法和决策参考,对城市中的示范性工程应用绩效评价有一定参考价值,也为完善DID模型的应用技术处理提供了新思路。从研究结果来看,ITS能够减缓交通拥堵、减少车辆行驶时间和距离、提高交通运行速度等,但是伴随着城市自身的快速发展,加之受较多因素影响,导致路网平均行车速度的改善并不明显或者某些城市的平均车速反而降低了,主要因为ITS产生的正向作用小于其他因素带来的负向作用,但不能否定ITS的贡献价值。
