基于甲型水驱曲线的 体积波及系数变化规律

朱圣举，张文博，朱 洁

(1.中国石油长庆油田分公司，陕西 西安 710018； 2.低渗透油气田勘探开发国家工程实验室，陕西 西安 710018； 3.陕西延长石油(集团)有限责任公司，陕西 延安 716000)

0 引 言

鄂尔多斯盆地北2区水驱砂岩油藏，采用反九点井网注水开发，开采层位为侏罗系延安组延9层，属低渗透油藏，其水驱规律符合甲型水驱特征曲线，但缺乏相应的水驱体积波及系数变化规律。水驱体积波及系数是指注入水波及到的油藏体积与油藏总体积之比，它是评价水驱油田开发效果的重要参数。求得波及系数的方法有概率论、量纲分析方法、图像处理技术、实验方法、经验公式法、数值模拟法、图版法[1]、理论分析法[2，3]，或仅对最大水驱波及系数进行评估[4]。然而，以上的研究大都在于求取最终的水驱波及系数，其变化规律仍不甚清楚。部分学者研究了水驱波及系数的变化规律，但是将水驱油效率当作一个定值的处理方法欠妥[5-6]；部分学者将水驱油效率作为变量处理，但是在处理油水相对渗透率比值时，忽视了水驱油效率与含水饱和度成直线关系的限制条件[7]，且以上研究均未涉及到已经广泛应用的甲型水驱特征曲线。基于此，从甲型水驱特征曲线入手，结合渗流理论，建立了一种新型水驱体积波及系数预测模型。采用鄂尔多斯盆地实际资料对模型进行验证，同时讨论了各参数对自变量(复合变量)的影响及模型的适用条件。

1 模型建立

在油水两相渗流的条件下，油水两相相对渗透率之比随出口端含水饱和度的变化关系在中间阶段为[8]：

(1)

式中：Kro、Krw分别为油相、水相相对渗透率；Swe为出口端含水饱和度；c1、d1分别为系数。

水油比为[9]：

(2)

式中：Fw为水油比；Bo、Bw分别为地层原油、地层水的体积系数；μo、μw分别为地层原油、地层水的黏度，mPa·s；ρo、ρw分别为地面原油、地面水的密度，g/cm3。

含水率与水油比的关系为：

(3)

式中：fw为含水率。

将式(1)、(2)代入式(3)，两边同时取自然对数后得：

(4)

水驱开发的水驱油效率为：

(5)

平均含水饱和度与出口端含水饱和度的关系为[20]：

(6)

式中：Sor为残余油饱和度。

将式(6)代入式(5)，得：

(7)

将式(4)代入式(7)，得：

(8)

令

(9)

(10)

则式(8)可改写为：

(11)

当水驱油藏开发到一定阶段时，会出现如下的函数关系式，即甲型水驱特征曲线[10]：

lnWp=B+ANp

(12)

式中：Wp为历年累计产水量，t；Np为历年累计产油量，t；A为斜率；B为截距，t。

对式(12)进行求导处理后，可得[11]：

(13)

式中：R为地质储量采出程度；c为斜率；d为截距。

地质储量采出程度可以分解为[16]：

R=EDEV

(14)

式中：Ev为水驱体积波及系数。

将式(11)、(13)代入式(14)中，可得：

(15)

将式(15)整理后，得：

(16)

令

(17)

(18)

则式(16)变为：

(19)

式(19)即为水驱体积波及系数随含水率的变化规律。由于式(1)只在中间阶段等式成立，因此，水驱体积波及系数预测公式在含水率达到某一值之后才能使用，这个值根据具体油藏来定。

2 实例分析

鄂尔多斯盆地北2区水驱砂岩低渗透油藏，油层有效厚度为6.3 m，空气渗透率为48.1×10-3μm2，孔隙度为16.0%，地层原油黏度为2.5 mPa·s，地层水黏度为0.5 mPa·s，地层原油体积系数为1.156，地层水体积系数为1.000，地面原油密度为0.85 g/cm3，地面水密度为1.00 g/cm3，束缚水饱和度为0.30，原始含油饱和度为0.70，残余油饱和度为0.285。由实验室岩心分析，其油水相对渗透率比值的自然对数与出口端含水饱和度在中间阶段呈直线关系(图1)：

ln(Kro/Krw)=9.5346-17.918Swe

(20)

式(11)中系数a、b求取方法如下：先根据实验室得到的相对渗透率数据，由式(3)计算出与不同出口端含水饱和度Swe对应的含水率值fw，由式(7)计算出与不同出口端含水饱和度Swe对应的水驱油效率值ED，再与实际开发油藏的含水率值进行一一对应，最后对出现直线段部分进行线性回归(图2)，则：

(21)

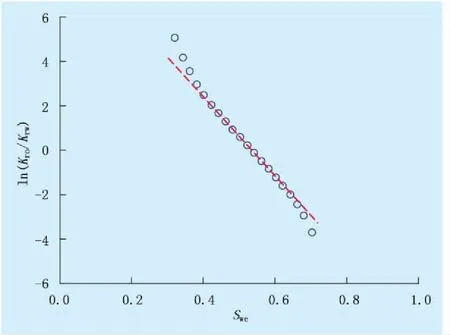
图1 ln(Kro/Krw)与Swe的关系

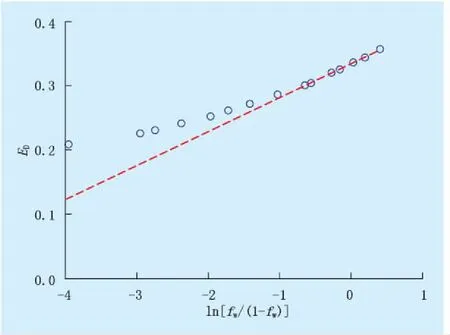
图2 ED与ln[fw/(1-fw)]的关系

式(13)中系数c、d求取方法如下：由实际油藏开发数据，作地质储量采出程度R与ln[fw/(1-fw)]关系曲线，对出现的直线段部分进行线性回归(图3)，则：

(22)

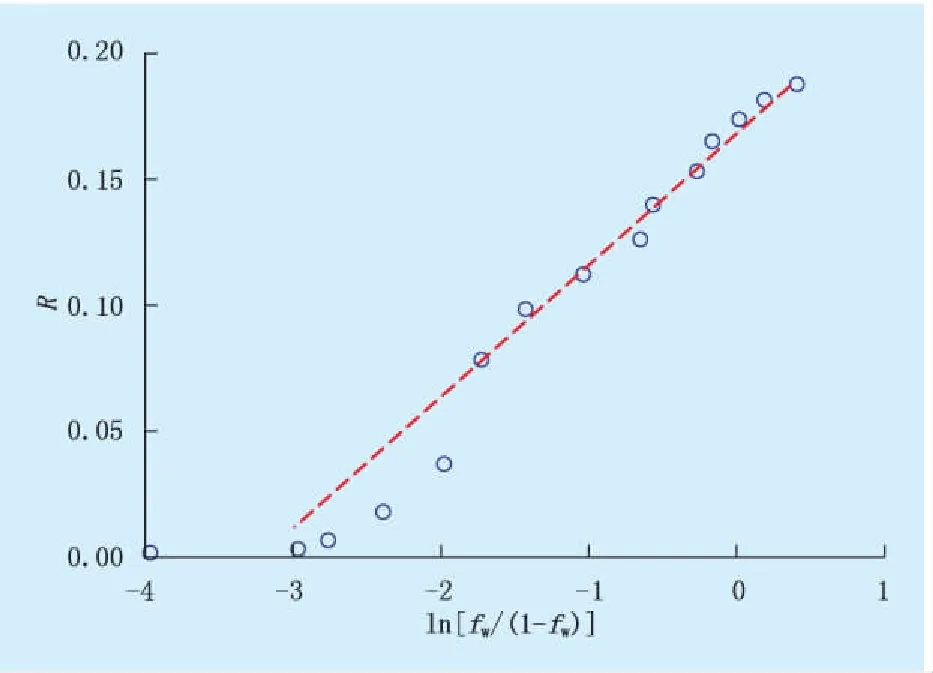
图3 R与ln[fw/(1-fw)]的关系

式(19)中系数m、n求取方法如下：由实际开发数据计算出不同含水率时的水驱体积波及系数Ev，将a=0.052 8、b=0.334 6代入式(19)中，作Ev与1/{ln[fw/(1-fw)]+b/a} 的关系曲线，对出现的直线段部分进行线性回归(图4)，则：

(23)

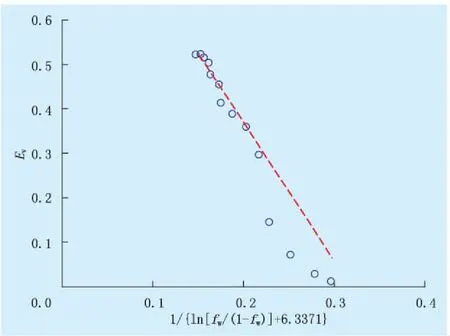
图4 Ev与1/{ln[fw/(1-fw)]+6.3371}的关系

运用式(23)，即可预测b2q油藏线性关系阶段内不同含水率时的水驱体积波及系数。如含水率为60%时，由式(23)计算的水驱体积波及系数为0.403 5；而由动态监测测得的纵向水驱波及系数为0.713 5、平面水驱波及系数为0.575 9，水驱体积波及系数为0.410 9。水驱体积波及系数预测值与实测值的相对误差仅为1.80%，表明该方法准确性高。

3 讨 论

鄂尔多斯盆地北2区水驱砂岩低渗透油藏，在含水率达到40%以后，才能用该模型进行预测，这是由相渗规律所决定的，如图1所示，ln(Kro/Krw)与Swe只在中间阶段呈线性关系。

式(19)中的a、b值作为固定参数参与到自变量1/{ln[fw/(1-fw)]+b/a}中，不会对自变量产生影响，这是由于a、b值主要来源于实验室岩心测试数据，即a、b值在油藏正式开发之前就已得出。

式(19)不能预测油藏的最终水驱体积波及系数，由图1可知，油藏在高含水阶段的相渗曲线发生了变化，即ln(Kro/Krw)与Swe不再呈线性关系。

4 结论与建议

(1) 基于甲型水驱特征曲线推导出的水驱体积波及系数Ev与由含水率及常数组合而成的复合变量1/{ln[fw/(1-fw)]+b/a}成线性关系，可以用于满足甲型水驱特征曲线的水驱油藏中间开发阶段的水驱体积波及系数评价及预测。

(2) 推导出的水驱体积波及系数预测模型的适用阶段，可以由实验室岩心测试结果确定，模型适用于油水相对渗透率比值的自然对数ln(Kro/Krw)与出口端含水饱和度Swe呈直线关系的阶段。

(3) 油藏开发的初期及晚期，由于ln(Kro/Krw)与Swe不呈直线关系，因此，不适于用文中模型来预测水驱体积波及系数，需要探索其他的方法。