浅谈练习课的教学设计

边敏珠

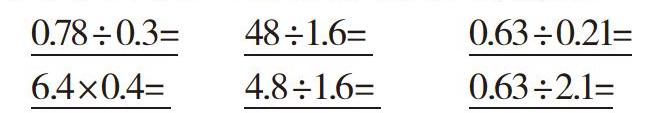
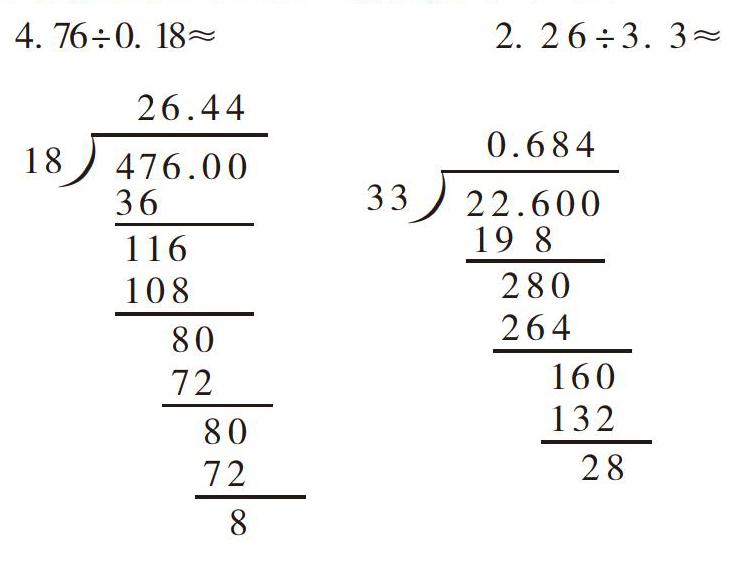
【摘 要】从现行的几套小学数学教材编排来看，练习课和复习课所占的比例均在50%以上。可见在小学数学教学中，练习、复习课的地位不容忽视。但在平时的教学中，练习课却一直没有受到足够的重视。很多教师都把练习课当做是作业课，认为练习课仅仅是对新授知识的简单重复 。因此对“如何上好练习课？”“如何让学生在练习课上有所发展？”普遍缺少思考，这也就形成了公开课一般不上练习课的现象。

【关键词】教学设计；练习目标

【中图分类号】G623.56 【文献标识码】B 【文章编号】1671-8437（2018）04-0160-02

其实练习课有着比新授课更为广阔的发展空间。练习课与新授课相比虽然缺少新鲜感，但同时也让学生消除了对知识的陌生感，不论从心理上还是从知识的储备上都为学生在这一知识上的进一步发展创造了更为稳固的平台。因此我们必须重视练习课的设计，为学生的进一步发展服务[1]。下面就《商的变化规律练习》为例谈谈对练习课的设计：

1 教学目标

练习课最大的特点不言而喻，是对新授知识的一次巩固和深化，并没有显见的新知识点。练习课是提高学生对新授知识的熟练程度，因此在确定练习课的教学目标时要从多个角度和维度去思考。

1.1 从学生的发展角度分析

首先可以从学生对新授知识的掌握程度和对所学技能的熟练程度上下功夫。如“通过练习，使学生能比较熟练地用四舍五入法求商的近似值。”

其次，可在学生对数学学习的情感态度上下功夫。如“让学生感受到简单的练习背后所蕴含的数学奥秘，从而培养学生多思多想、勇于探索的积极情感。”

最后应该从学生的思维发展上提出所要达到的目标，如“在各种情景和形式的练习中，发展学生从取值范围推测结果的能力[2]。”

1.2 从教材的角度分析

从原有知识、新授知识和后续知识之间的联系来确定教学目标。如在对本节课的教学时，提出让学生了解除了“四舍五入”法之外的几种取商的近似数的方法（进一法和舍去法）。

利用新授知识和日常的学习、生活之间的关系来确定教学目标。如“通过数学活动，让学生进一步感受求商的近似值的实际意义并学会灵活运用所学的知识解决实际问题。”

2 练习为目标服务

我们的教材在练习课的编排时存在一个普遍的问题，即练习形式比较单一，且与新课的练一练重复的较多。练习的功能很难充分发挥，因此我们在选择练习材料时应根据教学目标的需要选择合适的习题，使练习的功能得到最大限度的发挥。为此我认为，可从以下几个方面去选择材料：

2.1 选择内涵丰富的练习，为整合知识目标服务

如本节课的主要知识点是“用四舍五入法求商的近似值”，但这一知识又不是孤立的，它与以前所学的小数除法，以及求一个数的近似数等知识都有关联。因此，在选择练习材料时应充分发挥练习的“总结概括功能”，把相关联的数学知识作一次系统的整合。为此我在这节课的第一个环节设计了一道内涵丰富的口算训练：

0.78÷0.3= 48÷1.6= 0.63÷0.21=

6.4×0.4= 4.8÷1.6= 0.63÷2.1=

并通过“①说说带“ ”的两题你是怎么算的。②从第二、三两组口算中你想到了什么？”这两个问题回顾了小数除法的算法、算理和商不变性质、商的变化规律以及“一个数除以大于1的数商比被除数小，除以一个小于1的数商比被除数大”等规律。

另外在基本练习这一环节中我安排了两个练习，分别要求把商保留两位和三位小数，力求通过这两个练习，让学生进一步明确在求商的近似数时要比要求的小数位数多除一位这一知识要点。

2.2 选择有现实意义的练习，为提高学生的问题解决能力服务

课程标准要求学生“初步学会运用数学的思维方式去观察、分析现实社会，去解决日常生活中和其他学科学习中的问题，增强应用数学的意识”“体会数学与自然及人类社会的密切联系，了解数学的价值，增进对数学的理解和学好数学的信心”。那如何使学生在课堂上所学的知识与生活中的数学问题建立联系，并利用学生在生活中所积累的数学知识进一步促进对“学校数学”的理解和掌握，也是练习课要重点解决的问题。

因此，我在本节课的教学时，特别设计了两个与商的近似值密切相关的现实问题，以促进学生进一步感受求商的近似值的实际意义和应用价值：

第一：神州六号宇宙飞船89分钟绕地球一圈，约行42229千米，平均每分钟飞行42229÷89=474.4831460674157……千米，平均每秒钟飞行42229÷89÷60=7.9080524344569……千米。

第二：刘翔以12.91秒的成绩获得了男子110米栏的奥运会冠军，那刘翔平均每秒跑110÷12.91=8.52052672347……米。

另外，在基本练习中，将单纯的“保留两位小数和保留三位小数”两道练习赋于实际意义：

第一：当测量较长的路程时，如果对测量结果不要求十分精确时，可以用步测的方法。但测时必须知道自己在正常走路的情况下一步的长度，为此，小强和小明利用学校的60米跑道各走了一次，数得步数分别为95步和97步，请问这两位同学每一步的长度是多少？

第二：在科学实验中，“新空气”小组要将1.7千克水平均分在6只杯子中，問每只杯子可以分到多少千克水？如果将这些水分到7只杯子中，那每只杯子可以分到多少千克水呢？

通过两个具体的生活情境，使学生既巩固了用四舍五入法求商的近似数的方法，而且也培养了学生灵活应用数学的意识和能力，真正把数学学活了。

2.3 选择拓展性练习，为学生的思维发展服务

思维的发展是数学学习的重要目标，也是数学教学得以顺利进行的重要保障。如果没有思维的参与，数学课就失去了它的意义，同样在数学课中没有思维的发展，那数学也就失去了它生存的价值。而练习课在知识目标上的负担较轻，所以在学生的思维发展上要有所思考、有所体现。如在这节课中我设计了这样的练习，以拓展学生的视野和思维。

①你能根据下面的竖式将商保留三位小数吗？

②我们学校五、六年级共有学生319人，如果乘车组织秋游，每辆客车可以乘42人，需要多少辆车？（进一法）

看到这个信息你想说些什么？从中你能知道我们学校一共有多少学生吗？说说你是怎么想的？

当然面对不同教学内容，设计的方法也有所不同，这就要求我们要根据不同的教学内容和教学目标设计不同的练习。如利用多媒体等手段将静态的材料变成动态的画面；将封闭的问题设计成开放的活动等。

【参考文献】

[1]高芳.商的变化规律练习课教学设计[J].学园：教育科研， 2013（7）.

[2]黄红成.数学练习应注重训练与习得[J].教学与管理，2017（2）.