第四方物流多目标路径集成优化

任 亮，黄 敏，王洪峰，王兴伟

(1.东北大学信息科学与工程学院流程工业综合自动化国家重点实验室,沈阳 110819;2.武汉科技大学恒大管理学院,武汉 430081)

0 引言

随着电子商务的发展以及市场竞争的加剧，人们对物流服务的要求不断提高[1-2]。而传统的第三方物流(Third Party Logistics, 3PL)由于协作、整合能力不足等问题，很难满足当前激烈竞争的市场需求[3]。因此，以整合复杂供应链资源为主要目的的第四方物流(Fourth Party Logistics, 4PL)吸引了国内外的广泛关注[4-5]。

4PL是一个供应链的集成商，它对其内部和具有互补性服务供应商所拥有的不同资源、能力和技术进行整合和管理，以提供一整套供应链解决方案[6]。

路径问题是4PL优化中的关键问题[7]。4PL路径问题作用于4PL服务中的配送过程，直接影响客户的满意度和企业收益，许多学者对其进行了研究[8-9]。研究中多借鉴网络中基于图的研究方法[10]，主要有两种思路。第一种思路是在4PL网络上先依据一定规则选取路径，而后考虑在指定路径上的优化问题，即在指定路径上选择合作的3PL供应商[11]。Li等[12]将4PL优化分解为路线优化和供应商选择两个子问题，在最优路线计算完成后，用资源分配模型进行供应商选择。第二种思路是同时选择路径和供应商。Zhang等[13]将一个多重有向图中的每条边描述为一个3PL供应商，同时考虑路径和3PL供应商信息，清晰的描述了该问题，并以物流费用最小作为目标，基于Dijkstra方法快速求解了小规模的4PL路径问题。李锐等[14]用无向多重图描述4PL网络，同样将图中的每条边描述为一个3PL供应商，以最小化网络总成本为目标，研究了较为复杂的4PL网络设计问题。由于第二种思路从全局角度优化供应链，同时考虑了路径选择和供应商选择，可以获得较好的优化效果。

上述研究大多是针对单一目标问题，考虑物流费用最小或物流时间最短。但在实际物流运行中，往往需要权衡费用和时间因素。Liu等[15]从调度排序角度，以最小化总运输费用、运输时间以及拖期时间为目标，研究了多目标4PL优化问题。该文将物流任务分解成多阶段活动，研究了如何为物流活动选择合适的3PL供应商，但没有考虑运输过程中的路径选择问题。因此，本文从多目标的角度研究4PL路径问题，在集成考虑供应商选择优化和路径选择优化两方面的基础上，基于多重图，以物流费用最小和时间最短为目标，建立相应的优化模型。由于该问题属NP难问题，采用智能优化算法进行求解，数值实例表明了算法的有效性。

1 问题描述

本文要解决的问题是，在多条路径以及多个3PL供应商可供选择的情形下，为客户提供一套将运输任务从初始节点配送到目的节点的运输方案。方案要求满足一定的承载能力以及信誉约束，并最小化总运输费用以及总运输时间。

作为供应链的整合者，4PL集成供应链网络信息以及所有备选3PL供应商信息，为客户设计路径方案的同时需要选择3PL供应商。对于同样一段运输任务，基于不同的运输方式、不同的服务质量、需要时间的不同等特点，可能会有多个3PL供应商可供选择。综合到一张多重图上，可用具有多属性的边来描述，每条边表示在该段路径上提供服务的某个3PL供应商。4PL选择最优3PL供应商的组合，即多重图中选择最优路径，既考虑了路径优化，又考虑了3PL供应商的选择问题。

图1 4PL路径问题多重图Fig.1 Multi-graph of 4PL routing problem

数学模型建立如下：

(1)

(2)

s.t.

Pijk≥Pxijk(R)

(3)

Dijk≥Dxijk(R)

(4)

(5)

(6)

R={vs,…,vi,k,vj,…,ve}∈G

(7)

式(1)和式(2)为目标函数，表示最小化该运输任务的总运输费用和时间；式(3)表示被选3PL供应商的承载能力应满足客户需求；式(4)表示被选3PL供应商的信誉满足客户需求；式(5)和式(6)中xijk(R)和yi(R)为决策变量，分别表示边和节点是否被R选中；式(7)表示R为一条从vs出发并结束于ve的通路。

上述模型是一个多目标决策问题，且目标之间相互制约。众多可能解中，一般不存在一个优于其他所有解的方案，即并不存在绝对最优解。考虑到本问题是一个多重图上的NP难问题，选择智能算法与线性加权的选好函数法相结合的方法进行求解。在算法迭代过程中，每一代种群先进行支配关系比较，获得当前非支配集，而后再通过加权更新种群信息。并将选好权值设定为参数，针对决策者不同的目标权衡求解基于多重图的多目标路径优化问题。分别给种群非支配个体的两个目标加上权重系数α1和α2，目标函数可表示为：

min{α1C+α2T}

(8)

其中

α1+α2=1

(9)

(10)

(11)

由于通过权重系数α1和α2对费用和时间进行权衡，决策者可以根据侧重点的不同，对系数进行不同的权重分配，使之符合当前物流的实际运作。

上述模型是一个基于离散点、多属性的约束NP难问题，因此，采用对离散问题具有很好契合性的蚁群算法进行求解。

2 算法设计

蚁群算法是20世纪90年代发展起来的一种模仿蚂蚁群体行为的智能化算法。该算法引入正反馈并行机制，具有较强的鲁棒性、优良的分布式计算机制、易于与其他方法结合等优点[16]。尤其针对离散路径优化类问题，用蚂蚁觅食来模拟整个路径的寻优过程，具有很好的契合性。任务的起点为蚂蚁的出发点，任务的终点为蚂蚁食物所在位置，可行路为蚂蚁觅食可能行走的路径。因此，蚁群算法可以很好的模拟本问题的求解过程。

停滞现象是造成蚁群算法容易陷入局部最优的根本原因。针对此问题，本文采用动态调整选择策略的改进蚁群算法[17]，引入动态调整的选择策略，以提高蚁群算法的全局搜索能力和搜索速度。改进转移策略描述如下：

(12)

(13)

其中，NP为种群规模，NG为最大迭代次数，ng为当前迭代次数。i为当前节点标号，z为当前可供选择的第z条边。piz(ng)为第ng代时当前边(i,z)的选择概率。allowedi为节点i当前可供选择的边的集合。τiz(ng)为第ng代时当前边的信息素启发信息，ηiz为当前边的路径启发信息。ηiz=1/Ciz，其中Ciz为当前边(i,z)的费用，max{ηiz}表示启发信息ηiz的最大值。α和β分别为信息素和路径信息的相对重要程度。δ是选择策略调节系数，当δ为0时，χiz(ng)取值为1，此时该改进算法即退化为基本蚁群算法。qiz是从第一次迭代开始，经过边(i,z)的蚂蚁总个数。可以看出，当迭代过程趋于次优解时，虽然次优解上的信息素不断增强，但同时qiz也在不断增大，χiz(ng)值不断减小，其选择概率也不断减小，从而抑制因次优解上信息素过度剧增而导致的过早收敛，有利于算法的全局搜索。

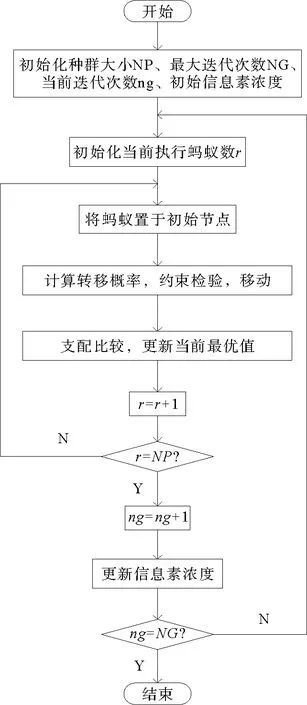
图2 改进蚁群算法流程图Fig.2 Flowchart of the improved ant colony algorithm

信息素更新规则如式(14)和(15)所示：

τiz(ng+1)=ρτiz(ng)+Δτiz(ng)

(14)

(15)

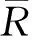
算法流程图如图2所示。

3 实例分析

假设某4PL公司承接了某一地区的供应链物流业务，需要执行从供应链起始节点到目的节点的运输任务。任务要求满足一定的承载能力以及信誉约束，并最小化总运输费用以及总运输时间。

3.1 参数分析

为测试算法性能，首先定义相关参数。算法运行100次，Best表示100次中的最好值，Bad表示最差值，Mean表示平均值，Time表示算法运行一次所需要的时间，S表示标准偏差，如式(16)所示。

(16)

算法参数取值均为经多次测试后，算法性能表现较好时的一组参数组合。测试过程如表1所示。表1为7节点实例中，当α1和α2分别取0.6和0.4时，测试改进算法中迭代次数对结果的影响。并且，从表1可以看出，针对小规模问题，算法能够很快求得所提出问题的最优解(此时问题规模较小，实验中通过枚举算法验证其为最优解)。

表1 迭代次数NG对结果的影响Tab.1 The effect of NG on the results

3.2 算法对比分析

如前文所述，改进算法在δ为0时，即转化为基本蚁群算法。因此，综合三个实例，在测得的较好参数组合情况下，δ分别取为0和测得值，即可对ACA和IACA进行对比，对比结果如表2所示。可以看出，对于小规模以及中等规模问题，两种算法均可以快速有效的求得较好解。对于较大规模问题，基于动态调整选择策略的IACA比ACA具有较明显的优越性。无论最差解、最好解，还是平均值，IACA均优于ACA。随着问题规模的增大，算法搜索需要的时间增长，标准偏差变大。针对较大规模问题，改进算法依旧能够有效的获得较好解。

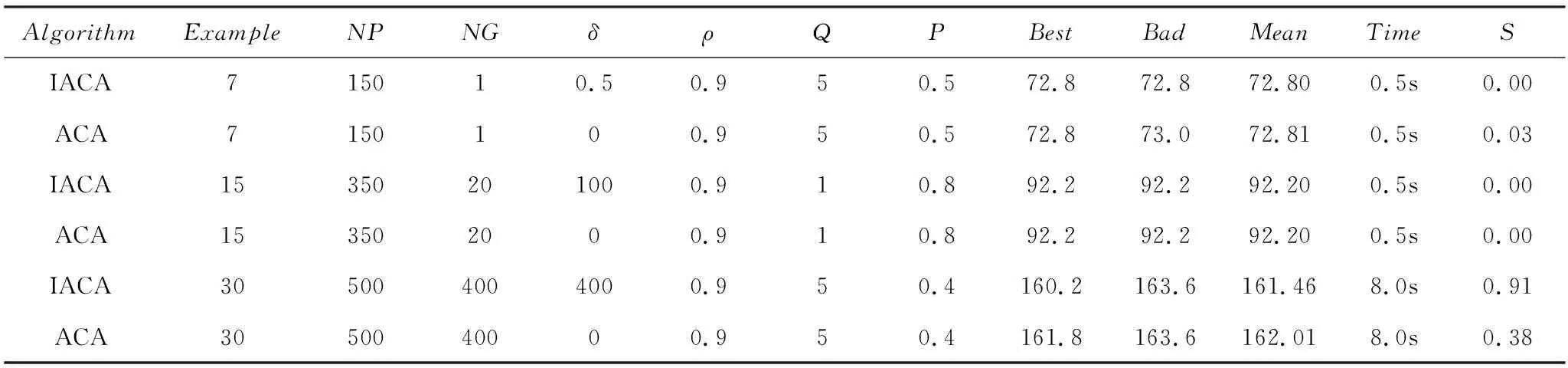
表2 ACA与IACA结果对比Tab.2 Comparison of ACA and IACA

3.3 多目标分析

本文考虑的是双目标优化问题，通过对权重系数α1和α2的调整，可对费用和时间进行权衡。根据决策者侧重点的不同，可以对该系数进行不同的权重分配。表3为15节点实例在不同α1和α2时的结果对比。可以看出，当费用和时间权重系数中有一个为0时，该问题转化为单目标优化问题。随着费用权重系数不断变大，决策者对费用的重要性感知不断增强，解的目标值逐渐增加。在不同权值分配下，改进算法均能快速、有效获得问题的较好解。

表3 加权系数对结果的影响Tab.3 The effect of weighting coefficient on the results

4 结语

本文针对4PL路径问题，集成考虑了路径选择优化和供应商选择优化两方面的问题。建立了以物流费用最少和运输时间最短为目标的数学模型，为第四方物流路径优化提供了建模工具。进而，采用改进蚁群算法对模型进行求解，并通过实例与基本蚁群算法进行对比。对比结果表明，当问题规模较小时，两种算法对该类问题都具有较好的效果。随着问题规模的增大，改进算法体现出其优越性。针对决策者不同的决策偏好，算法都可以快速有效的帮助决策者做出最终决策，并协助决策者设计分析偏好，从而为上述问题提供了有效的求解工具。