平面位势问题的简单解边界元法
2018-09-04许文政张耀明
许文政,张耀明
(山东理工大学 数学与统计学院,山东 淄博 255049)
边界元法是分析科学和工程应用问题的强有力的数值模拟工具,广泛应用于位势流,弹性静、动力学,声传播等线性问题及各种非均匀材料与非线性问题[1-6].但是,不同于域型方法,边界元法需要计算奇异核积分,它的有效计算是边界法成功实施的关键.时至今日,这方面的研究仍在进行中[1-3].
现有许多有效计算奇异积分的方法[7-9].大致可分为直接计算方法和间接计算方法两大类[10-20].其中,Guiggiani等[10]提出的方法具有代表性,该方法在内蕴坐标系的参数平面内操作,能计算各种阶奇异积分.该方法需要将被积函数中的每个量展成单元局部距离Ω的泰勒级数,因此需要许多复杂的推导工作和与单元有关的计算.高效伟[11]也提出了一种计算奇异积分的一般性算法,它将积分核中的非奇异部分表示成在内蕴坐标系统下的局部距离参数的幂级数,然后解析计算.确定幂级数的系数时,需要求解线性方程组,而且这样的操作每个单元都需要.间接计算方法主要是通过建立各种规则化边界积分方程,来间接计算CPV和HFP积分.包括直接变量规则化边界积分方程和间接变量规则化边界积分方程[7-9,15-20].
不同于已有的工作,本文提出了一个新的计算强奇异积分的方法,称为简单解法.它利用简单解过程,获得强奇异积分值,无需直接计算积分,也无需建立规则化边界积分方程,因此方法具有理论简单、计算效率高、结果准确等优点.此外,方法能够计算任何边界通量∂u/∂xi(i=1,2).该方法容易跟随和拓展到其他如弹性力学问题、Stokes问题、Helmholtz问题等.
1 基本概念
本文假定Ω是R2中的一个有界区域,Ωc是它的补域,Γ=∂Ω是它们的边界.n(x)是区域Ω的边界Γ在x点处的单位外法向量.位势问题的基本解是
(1)


(2)
2 简单解法
Ω内的位势可表示为[17]

(3)
(4)
对方程(4),令y→Γ,可获得如下边界积分方程
(5)

(6)
为了能够更清楚地表述问题的本质,采用方程(6)的离散化形式.将边界Γ分割成N段(Segment),并假定y在第l段上,即y∈Γl,并记为yl,于是有
(7)
式(7)右端第一项中的积分均为正常积分,因此问题的关键在于如何估计式(7)右端第二项积分.若记
方程(7)可写为
φ(yl)A,yl∈Γl
(8)
当常元插值(常单元)被采用时,方程(8)可写为
yl∈Γl
(9)
这里φm表示密度函数φ在第m个节点上的值.为了确定(7)式中的A,提出一种简单、高效、准确的简单解法:
(1)对于有限域Ω,引入如下简单解
u(x)=x1+x2+1
(10)
(2)对于无限域Ωc,引入如下简单解
(11)
这里(a,b)是Ωc外的任一点.
注:原则上,简单解可以任意选取.对于内边值问题,简单解只需满足Laplace方程;对于外边值问题,简单解除满足Laplace方程外,还需满足无穷远边界条件.
方程(4)的离散化形式
l=1,…,N
(12)
这里φm是边界密度函数φ(x) 在第m个单元Γm(m=1,…,N)上的节点处的值.
对于有限(无限)域问题,将简单解式(10)(或式(11))代入方程(12)中,可求得密度函数在N个节点处的值φm,m=1,…,N.然后,将所求得的密度函数解φm及简单解式(10)(或式(11))代入方程(9)中,即可求得A.
以上方程经过适当的组合变形后,可适用于任何边界条件的边值问题.
3 数值算例
利用三个数值算例,以验证本文算法的精确性、有效性及收敛性.所有算例中,边界离散单元的边界量采用常元插值,单元几何边界采用精确单元L2范数下的相对误差定义为
Relative error =
(13)
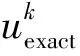
算例1首先考察一个具有Dirichlet不连续边界条件的的稳定温度场问题.计算域是[0,1]×[0,1],边界条件是
(14)
问题的解析解是
u(x1,x2)=
(15)
其中
(16)
计算时,边界单元数是80个.图1(a)和图1(b)分别描述了解析法和本文数值法获得的场位势的等值图,可观察到,本文数值解和解析解比较吻合.为了进一步考察本文方法的准确性和有效性,选择1 600个计算点均布在区域0.15≤x,y≤0.85内,图2给出了这些计算点上的场温度数值解的绝对误差曲面.从中可以看出,尽管具有很少的边界单元数,本文获得的数值结果仍然相当准确,表明本文给出的方法能够有效地求解具有不连续Dirichlet边界条件的边值问题.意味着,本文计算强奇异积分对角元的方法是非常有效的.
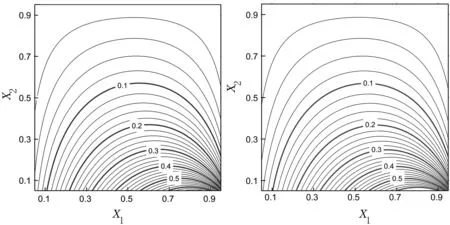
(a) 解析解 (b) 数值解图1 场位势解Fig.1 The field potential solution

图2 边界通量解的收敛曲线Fig.2 Convergence curves of boundary flux solutions

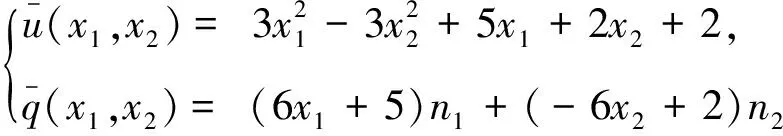
(17)

图3 计算域Fig.3 Problem sketch
计算时,外边界Γ1离散为36单元,内边界离散为24个单元.表1给出了沿x轴一些域内点处温度的数值结果;图4(a)和(b)分部描述了边界Γ1上的法向通量解和边界Γ2的温度解的相对误差.从中可看出,即使使用很少的单元数,数值解已相当地准确.
表1 内点温度解
Tab.1 Temperature solutions on internal points

内点精确解数值解相对误差(6.0, 0.0)0.1400000×1030.1399699×1032.149503×10-4(7.0, 0.0)0.1840000×1030.1839418×1033.163785×10-4(8.0, 0.0)0.2340000×1030.2339130×1033.719932×10-4(9.0, 0.0)0.2900000×1030.2898743×1034.333464×10-4

(a) 通量q

(b) 温度u图4 边界量数值解的相对误差Fig.4 Ralative error of boundary temperature uand flux q
算例3考虑不规则区域上,具有混合边界条件的温度场问题,如图5所示.边界Γ由两部分构成,即Γ=Γ1∪Γ2,其中
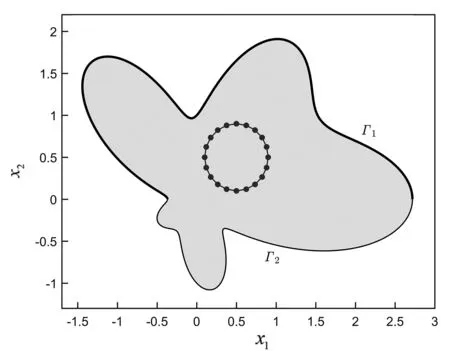
图5 计算域Fig.5 Problem sketch



问题的解析解是如下振荡调和函数
u(x1,x2)=ex1+3cosx2
(18)
图6 给出了边界Γ上的位势函数u的图像,从图中可观察到,u的最大值大于300,最小值小于-20,表明位势边界函数u具有很强的振荡性.
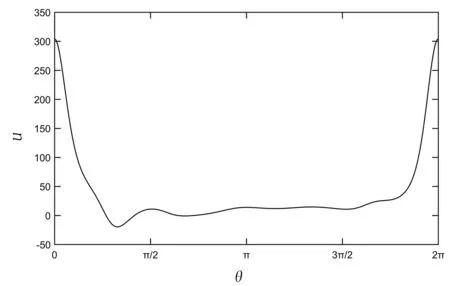
图6 边界Γ上的位势函数Fig.6 Potential boundary function on Γ
20个域内计算点均布在中心在(0.5,0.5),半径是0.4的圆周上,如图5所示.图7描述了这些计算点上的温度数值解u的收敛曲线,图8给出了边界Γ1上的通量和Γ2上的温度数值解的收敛曲线.从中可看出,不论是内点还是边界点,随着边界单元数的增加,相对误差迅速减小,可见本文方法在求解具有振荡解析的问题时仍具有很好的收敛特征.表明本文计算强奇异对角元的方法是非常有效的.

图7 内点温度数值解的收敛曲线Fig.7 Convergence curves of temperature solutions at internal points
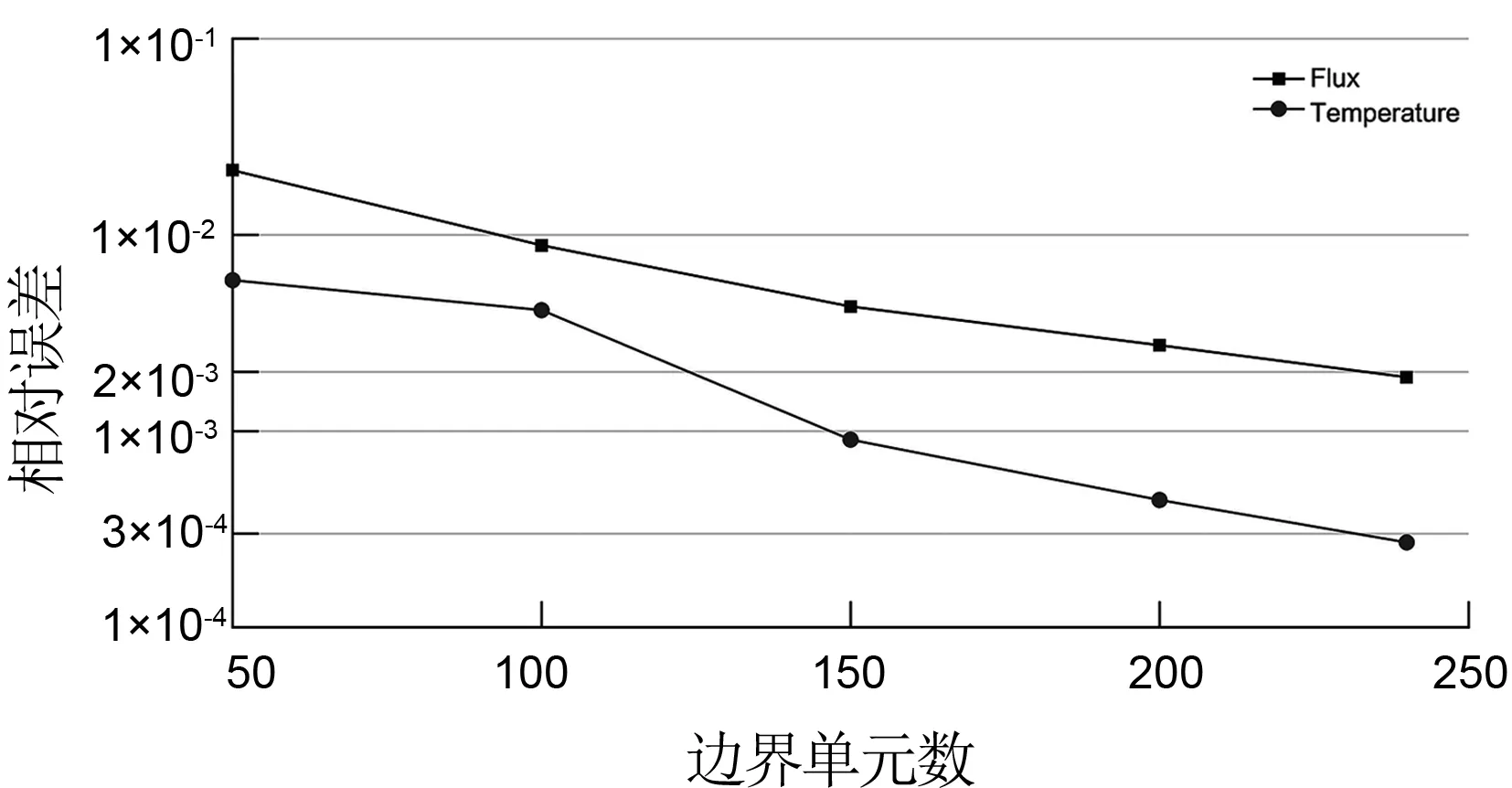
图8 边界温度u和通量q的收敛曲线Fig.8 Convergence curves of boundary temperature uand flux q
4 结束语
本文提出了计算强奇异积分的简单解法,适用于任何边界通量的计算,具有数学理论简单,程序设计容易,计算准确性高,容易跟随和推广等优点.数值算例验证了方法的有效性,表明本文方法能够有效准确地计算强奇异积分的对角元.
