碰撞阻尼器的颤振行为研究

杜妍辰， 王 彬

(上海理工大学 医疗器械与食品学院，上海 200093)

碰撞阻尼属于振动的被动控制技术，它利用振动过程中自由质量(冲击器)与主系统的碰撞来控制主系统的响应。碰撞阻尼器构造简单、成本低廉、易于实施、无需外电源、适合在恶劣环境下使用并且减振效果良好。关于碰撞阻尼的研究在最近得到了迅猛的发展，目前有代表性的碰撞阻尼包括：单体碰撞阻尼[1-4]、豆包碰撞阻尼[5]、多体碰撞阻尼[6]、颗粒碰撞阻尼[7-13]、非阻塞性颗粒碰撞阻尼(Non Obstructive Particlc Damper, NOPD)[14-15]、带颗粒减振剂的碰撞阻尼[16-20]等。

虽然碰撞阻尼器种类繁多，但他们之间存在着共性。从减振机理上看，主要的原理是动量交换和碰撞耗能机理；从理论研究方法上看，大部分沿用或借鉴了单体碰撞阻尼的模型，因此，单体碰撞阻尼是这一领域研究的基础模型。现有的关于单体碰撞阻尼的研究成果认为：每周期两次对称碰撞是碰撞阻尼器中典型的和具有较好减振性能的运动模式；但这种好的减振效果只在共振点附近出现，远离共振点的地方，则效果不好甚至出现放大的情况。因此，当使用频率位于一段频率范围内而非仅在共振点附近时，现有的理论分析认为每周期两次对称碰撞所取得的减振效果并不理想。作者通过实验研究发现，当恢复系数较低时，碰撞阻尼器频率适应范围宽，即在很大的一段频率范围内均有较好的表现，这与以往关于单体碰撞阻尼的理论研究结论有较大的差别。通过数值模拟考察其运动模式，发现在减振效果较好的运动轨迹中，存在颤振和黏滞的现象，即颤振和黏滞有可能是碰撞阻尼器取得良好减振效果的新的有效的途径。所谓颤振，是指自由质量在短时间内与主系统之间发生很多次甚至无穷次碰撞的情况。所谓黏滞，是指自由质量与主系统同步运动的情况。关于碰撞阻尼器中的颤振研究，目前还没有任何报导。

在两种情况下，颤振可以直接转化为黏滞，一种是恢复系数为零的情况，此时，没有颤振，碰撞后直接产生黏滞；另一种为颤振结束后自由质量与主系统相对运动为零，产生了黏滞，这种颤振称为“完全颤振”，而颤振结束后自由质量与主系统相对速度不为零，则不会产生黏滞，这种颤振称为“不完全颤振”。国际上，关于颤振方面的研究是从Budd等[21]和Toulemonde等[22]以及Wagg等[23]开始的，重点是对擦边分岔及引发的运动周期和碰撞次数的变化以及多峰值等现象做了研究。其他关于碰撞颤振的报道还非常有限，Hös等[24]研究了由擦边引起的减压阀与底座间的自激振动，发现低的流速会引发颤振，阀门预紧力是引发颤振的另外一个因素；Demeio等[25]研究了倒立摆碰撞中颤振持续时间的近似计算方法，研究表明，颤振持续时间主要与振幅相关，与激振频率和阻尼比关系不大；Singh等[26]研究了双摆碰撞问题、Davis等[27]研究了一个摆与旋转的障碍(moving obstacle)之间的碰撞，Wagg等[28]研究了一根悬臂梁与一个刚性障碍的碰撞，在这些不同类型的碰撞过程中，均发现了颤振和黏滞运动。目前关于颤振和黏滞的研究，均未涉及到阻尼器，还没有发现关于碰撞阻尼器中颤振方面的报道。一方面，这些系统大多有固定的约束，其振幅已被限定在一定的范围内，另一方面，关于碰撞阻尼器的研究大多关注每周期两次的对称碰撞，几乎都没有涉及到颤振。由于碰撞阻尼器中的约束是一个自由质量，其位置并不固定，因此，关于碰撞阻尼器中的颤振研究与现有的研究会有较大的不同。

本文以经典的碰撞阻尼器为模型，分别通过理论推导和数值模拟验证两个方面对系统的颤振行为进行研究，确定了系统的颤振持续时间和颤振完成点，对不同参数条件对颤振行为的影响进行了研究。

1 系统力学模型及运动微分方程

以经典的碰撞阻尼减振器为模型，研究碰撞阻尼减振系统的动力学行为。系统的简化动力学模型如图1所示。

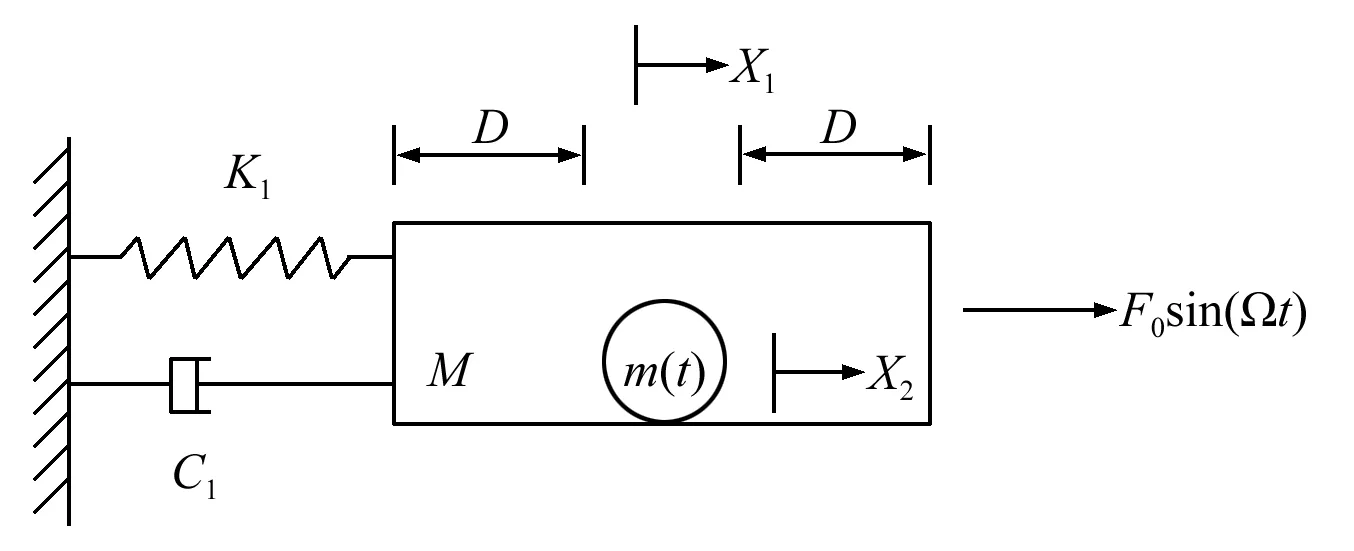
图1 碰撞阻尼器模型示意图Fig.1 A model for Impact damper

图1是多体碰撞阻尼器的简化力学模型，其中的自由质量以m(t)来表示，主系统由主质量M，弹簧刚度K1及阻尼C1组成，在外加激振力F0sin(Ωt)的作用下产生振动。自由质量m(t)置于主系统M内部，在振动过程中自由质量只在主系统M内部做水平方向的运动，且当自由质量m(t)与主系统M的相对位移为D时，二者发生碰撞，然后以新的速度反方向运动，如此反复碰撞，通过动量交换使系统部分机械能转换成内能，达到减振的目的。

取系统的中心位置为坐标原点。当自由质量m(t)与主系统M发生相互碰撞，改变速度方向后，又以新的初值运动，然后再次碰撞，如此反复。为方便计算，采取以下几个基本假设：

(1)在两次碰撞过程之间，主系统与自由质量之间无摩擦；

(2)将多个介质简化为一个球体，即质量为m(t)；

(3)在一个激励周期内发生n次对称性碰撞，且碰撞发生在瞬间，因而碰撞只改变m与M的速度，不改变其位移(满足动量守恒定律)；

(4)碰撞时非弹性的，用恢复系数R加以表示；

(5)只考虑水平方向的碰撞。

图1所示的碰撞阻尼系统，在两次碰撞过程之间，描述系统运动的微分方程为：

(1)

(2)

当X1-X2=D时，M与m(t)发生碰撞，且碰撞被理想化为一个不连续的过程，由动量守恒定律及碰撞恢复系数R的定义可得：

(3)

(4)

自由质量m(t)是时间的函数，具有时变性。因为对于系统来说，自由质量m(t)引起的非线性动力学行为变化是缓慢的，因此自由质量m(t)可以用其在一个振动周期内的平均值代替，即：

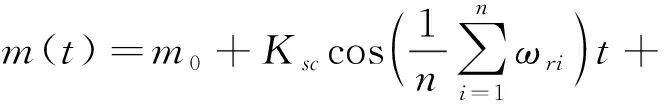
式中：m0为质量常数；Ksc，Kss为亚谐碰撞的余弦和正弦项系数；Kic，Kis为余弦和正弦谐波项系数。

事实上，亚谐碰撞频率常常是系统激振频率的整约数，即

(5)

式中:n为整数。

为简便计算，这里仅计入常数项和亚谐波项，略去谐波项部分，并化简得

m(t)=m0+kssin(ωat+φ)

(6)

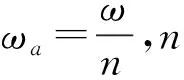
在振动过程中，自由质量m(t)与主系统M相互碰撞产生冲击力，系统的运动可以考虑为一个分段线性过程。根据碰撞阻尼振动系统自身的特性，对图1所示的碰撞阻尼器模型做出如下修改：

(1)相互碰撞之间无摩擦，且只考虑水平方向上的振动。

(2)当m与主系统发生碰撞时，在碰撞点产生一个局部变量，且碰撞时主系统M对碰撞体m具有刚度制约作用，因此用弹簧刚度K2来模拟这一过程。

(3)碰撞恢复系数，采用黏性阻尼C2来实现。

基于上述假设，可将上图所示的碰撞模型简化为图2所示的两自由度振动模型。

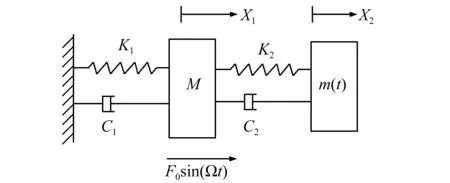
图2 两自由度碰撞振动系统示意图Fig.2 Schematic diagram of the impact dampingsystem with two degree of freedom

图2是由碰撞阻尼器模型简化而来的两自由度碰撞振动系统的模型示意图，主系统M和自由质量m(t)分别通过弹簧刚度K1，K2和线性阻尼器C1，C2连接于固定约束端，主系统受到水平方向的F0sin(Ωt)的作用，当主系统M和自由质量m(t)的位移差等于D时，二者发生碰撞。

系统的动力学方程为：

(7)

(8)

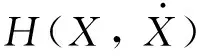
式中：D为间隙。

适当的选择K2，非线性弹簧可以模拟任意大小的刚性屏障，常数C2H乘积的值则可以恰当地模拟各种弹塑性碰撞，只要选取适当的C2便可以确定任意恢复系数R的值。

化简方程(7)和(8)可得：

(9)

(10)

上述方程中“·”表示对时间t的求导。

引入无量纲参量：

化简得到系统的无量纲运动微分方程：

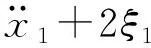
(11)

(12)

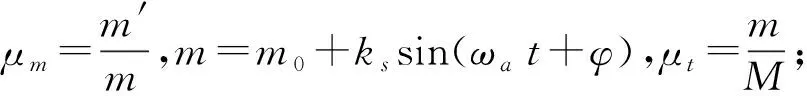
式中：符号“ ′ ”表示对无量纲时间T的求导。

2 颤振现象的理论推导

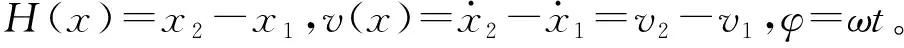
以自由质量m的运动状态作为讨论对象，碰撞面∑(x,t)={x│H(x)=d,v(x)=0}。第一次碰撞后m的相对位置和速度为：

X1(x,v)=x+W(x)v，V1(x,v)=-rv

(13)

继续讨论下一次碰撞后m的状态：

(14)

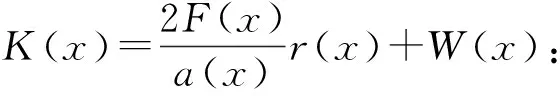
X3(x,v)=x+K(x)v+O(v2)，V1(x,v)=rv

(15)

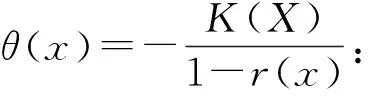
x=X4(x*,v)=x*+θ(x*)v+O(v2)

(16)

且有X3(X4(x,v),v)=X4(x,V3(X4(x,v),v))，代入v(x)表达式可以求得

(17)

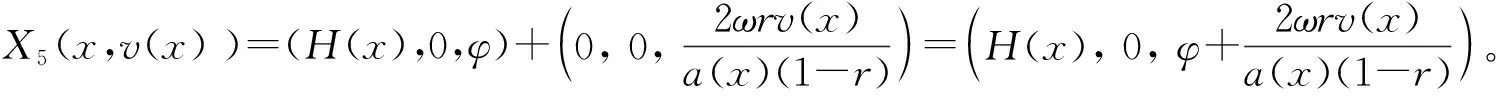
3 颤振现象的数值模拟

在上一节中对两自由度碰撞振动模型的颤振现象进行了详细的理论计算和推导，得到了颤振完成点和颤振过程所经历的时间。颤振可以分为“完全颤振”和“不完全颤振”，在颤振结束后自由质量与主系统相对运动为零，产生了黏滞，这种现象称为“完全颤振”；而在颤振结束后自由质量与主系统相对速度不为零，则不会产生黏滞，这种现象称为“不完全颤振”。

为了对此类碰撞振动系统的颤振现象有更加深入的研究，本节将通过四阶Runge-Kutta法对其进行数值模拟。

对方程(11)～(12)进行降阶处理，得到了以下的四维等价系统：

(18)

其中，

为简化计算可取：

则方程(18)中的参数可以写为：

在其他参数一定的情况下，首先以间距d作为控制参数，得到主系统M的位移在d=0～2区间内变化的分岔图。

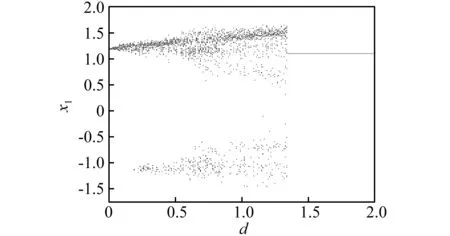
图3 x1最大值随间距d的分岔图Fig.3 Bifurcation diagram of maximum x1with distanced

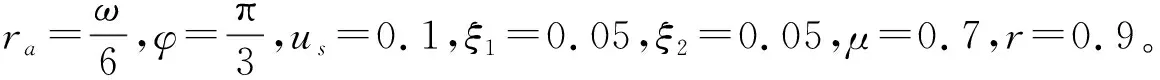
由上述讨论结果可取d=0.2，以系统的激振频率ω作为控制参数，利用四阶Runge-Kutta法进行数值模拟进一步研究系统的颤振现象。图4为频率ω=0～5范围内，主系统M的位移随其变化的分岔图。

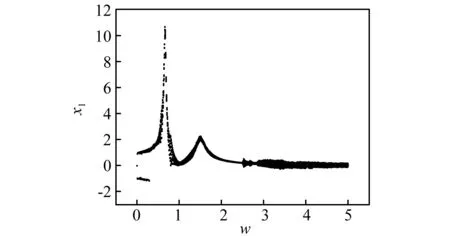
图4 x1最大值随频率ω的分岔图Fig.4 Bifurcation diagram of maximum x1with frequency ω

由分岔图4可以看出，主系统M的位移随着激振频率ω的逐渐增大发生了明显的变化，且在ω=0～0.35的范围内系统发生了颤振行为。

由自由质量m的时域变化图5,6,7可以看到当ω分别取0.2,0.25,0.3时m的相对位移和相对速度随时间变化的情况。由图5(a)可以发现，当ω=0.2时，颤振现象约从t=332 s开始，持续时间约为11 s，表现在图中为出现了一条平行于x2-x1=0.2的线段，且在图5(b)中自由质量m的相对速度趋于0，也就是完全颤振完成的状态。同样地，由图6(a)可以发现，当ω=0.25时，颤振现象约从t=316 s开始，到t=327 s结束，持续时间也约为11 s。进一步观察图7(a)，当ω=0.3时，系统虽然也发生了颤振现象，但是与图5(a)和图6(a)相比较可以发现，在颤振结束时并未出现一条平行于x2-x1=0.2的线段，且其相对速度的时域图7(b)与图5(b)和图6(b)相比较也可以更为清晰的看出完全颤振与非完全颤振的分别。

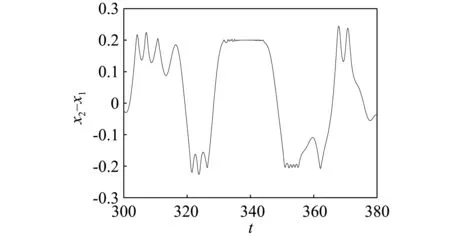
(a)位移时域图

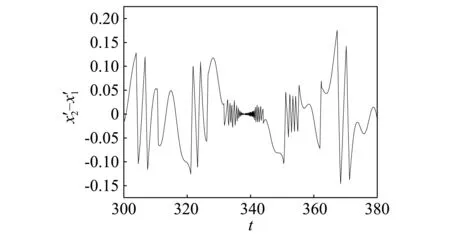
(b)速度时域图图5 ω=0.20时自由质量m的时域变化图Fig.5 Time-domain diagram of m with ω=0.20

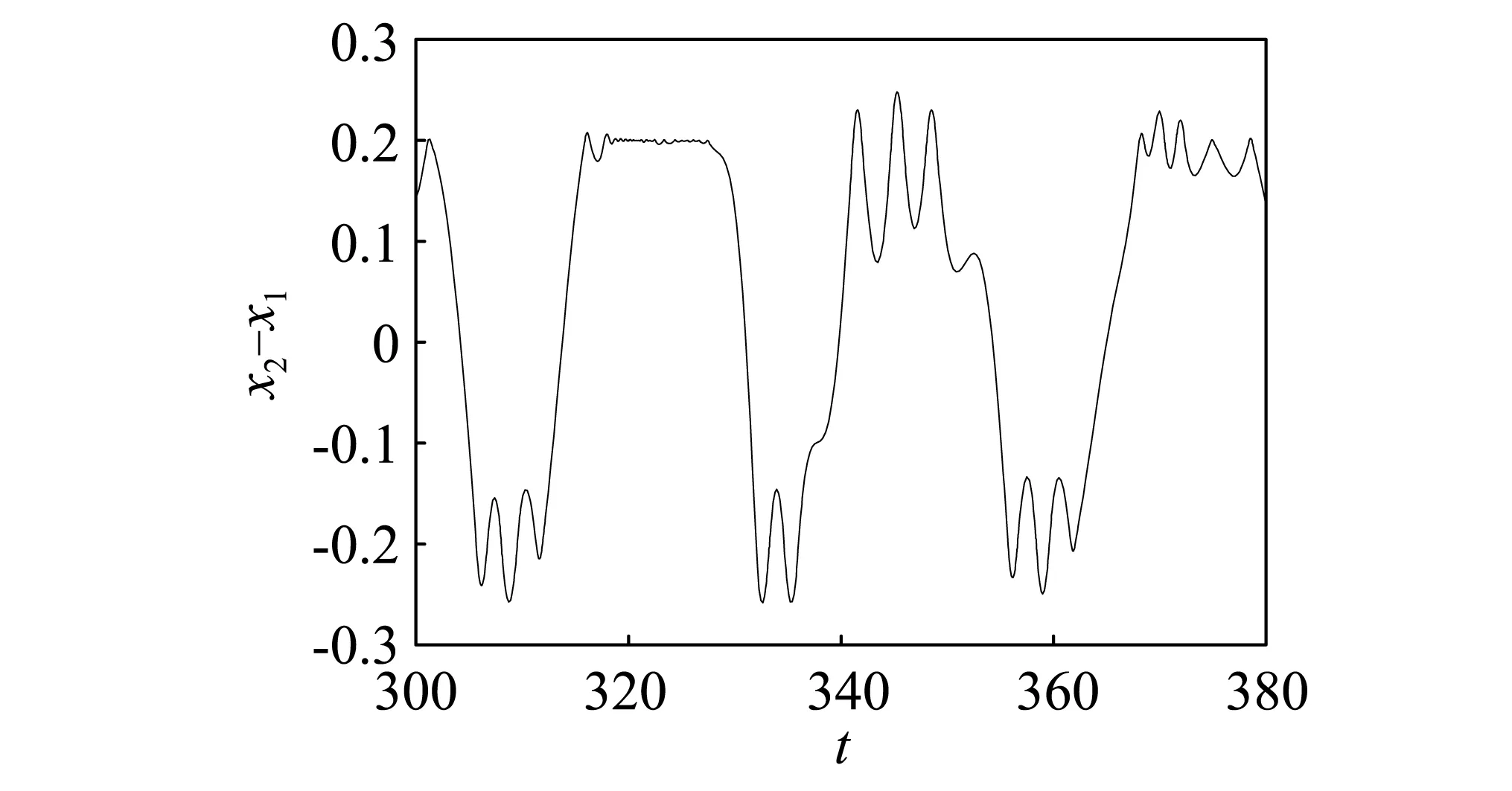
(a)位移时域图

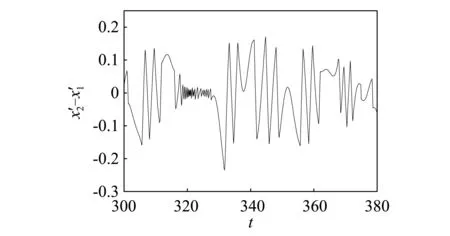
(b)速度时域图图6 ω=0.25时自由质量m的时域变化图Fig.6 Time-domain diagram of m with ω=0.25

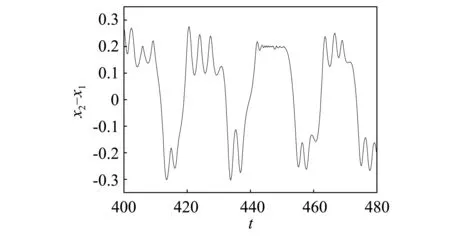
(a)位移时域图

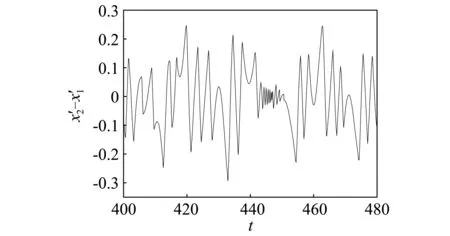
(b)速度时域图图7 ω=0.30时自由质量m的时域变化图Fig.7 Time-domain diagram of m with ω=0.30

为对完全颤振和非完全颤振的运动现象有更深入的认识，下面分别对图5和图6进行局部放大，得到ω=0.2，0.25时自由质量m的时域变化放大图。

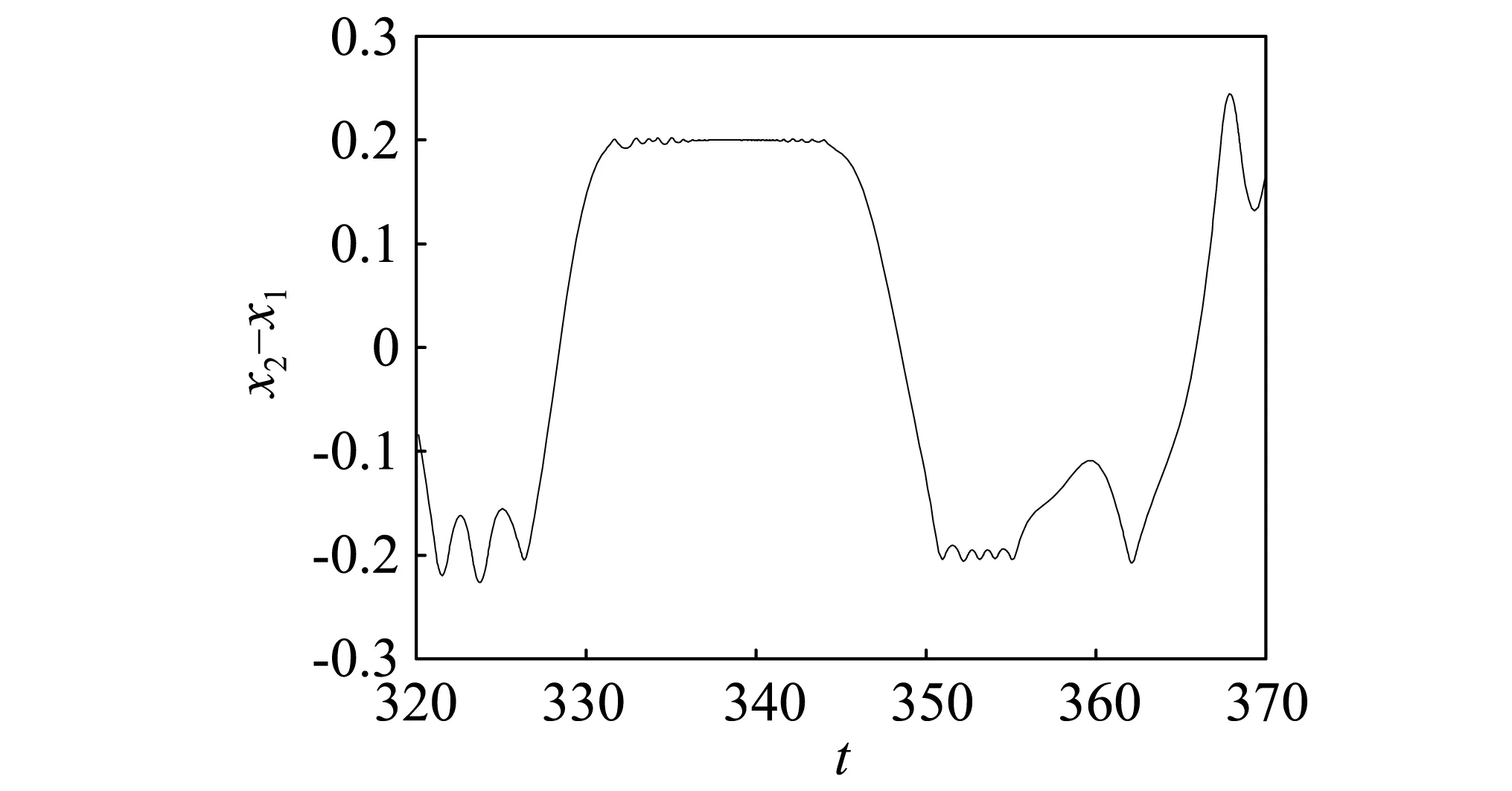
(a)位移时域图

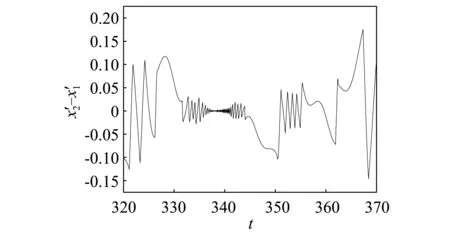
(b)速度时域图图8 ω=0.20时自由质量m的时域变化放大图Fig.8 Enlarge time-domain diagram of m with ω=0.20

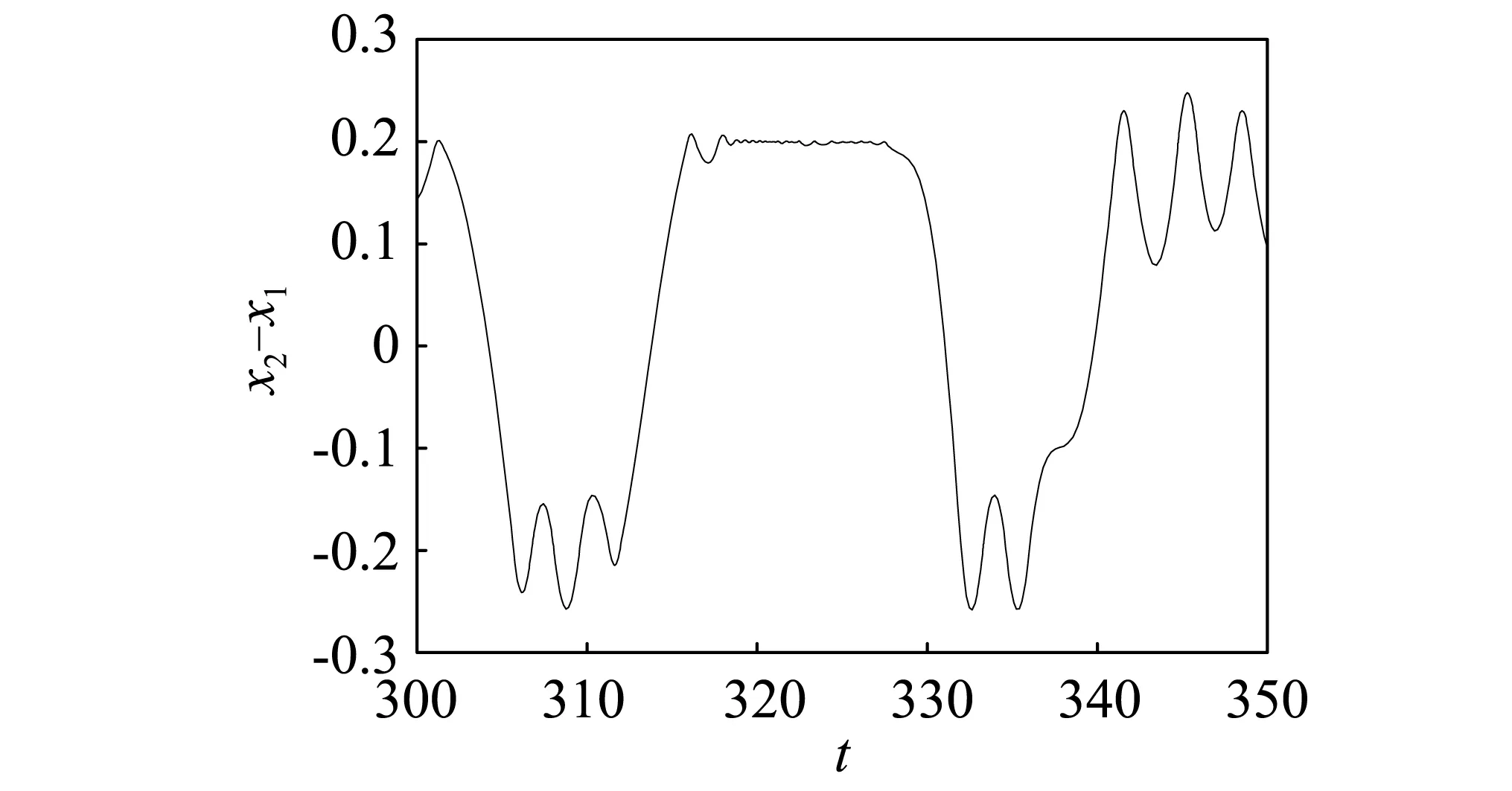
(a)位移时域图

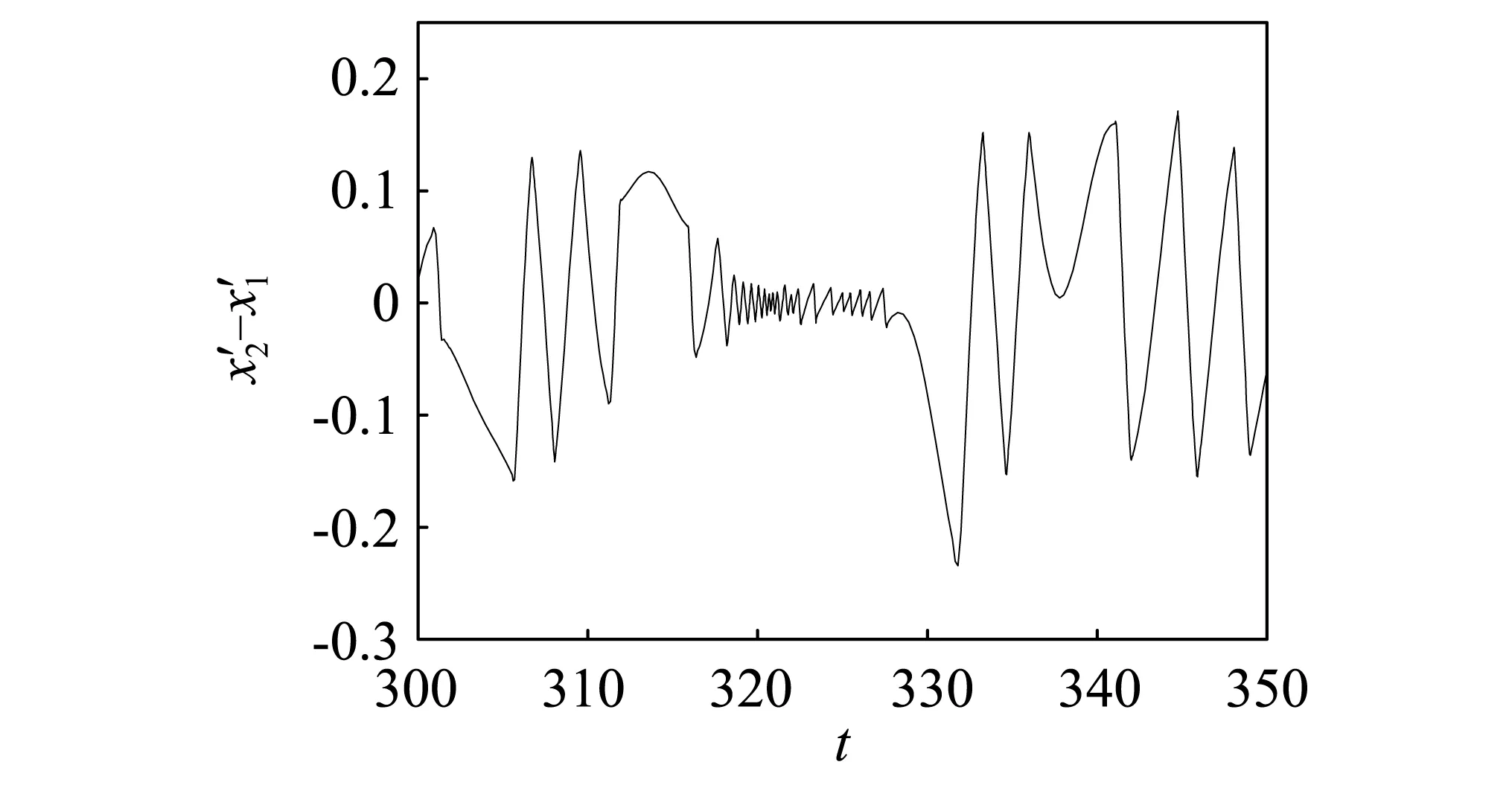
(b)速度时域图图9 ω=0.25时自由质量m的时域变化放大图Fig.9 Enlarge time-domain diagram of m with ω=0.25

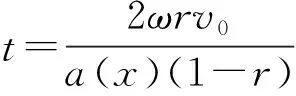
4 结 论

本文针对由经典的碰撞阻尼器简化而来的两自由度碰撞阻尼振动系统，通过理论推导和数值模拟相结合的方法，计算得到了系统的完全颤振持续时间和颤振完成点，并借助Matlab编程得到的分岔图和时域图，深入研究了不同参数条件下系统的颤振变化过程，计算结果与理论推导得到的结论一致，证明了理论计算的正确性。本文主要结论如下：

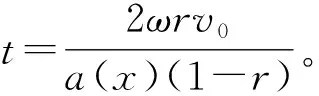
(2)由不同参数条件下自由质量m的相对位移和速度时域图可知，在经历了一段时间的复杂运动响应后发生颤振运动，且颤振的持续时间和结束状态与理论推导结论相吻合。

(3)系统经历了完全颤振和不完全颤振，且其时域图清晰地说明黏滞是完全颤振收尾时的重要特征。