面向公路检测的多轴稳定平台运动学建模与等效变换
2018-09-03罗二娟
罗二娟
(山西省交通科学研究院 黄土地区公路建设与养护技术交通行业重点实验室,山西 太原 030006)
0 引 言
为满足交通基础设施定期检测、维修的需求,各种多功能检测车应用而生[1-2]。为提高检测车的工作效率和检测精度,数字相机、激光传感器等高精度仪器已成为不可或缺的重要装备[3-4]。但是,在周围车流量、发动机振动、路面颠簸等环境扰动的作用下,车辆会产生多自由度摇摆运动,给车载设备带来严重影响[5]。因此研发能够快速补偿车辆多维扰动的装置已成为当前交通智能装备发展的关键。
并联机构具有多轴联动、结构紧凑、运动精度高、动态响应好等优点,是研制载体式多轴稳定平台的理想机构学模型[6-9]。公路检测用多轴稳定平台是一个处于非惯性系中的复杂多刚体系统,应用传统运动描述方法建立多轴稳定平台的运动学模型时,推导过程繁琐,数学模型复杂,更无法实现基于运动学模型的高精度实时伺服控制[10-13]。同时,样机试验研究是开展稳定平台应用的前提,而在试验初期,多轴稳定平台样机无法在车辆等非惯性系中开展各项功能性测试,只能在地面等惯性系中开展。这就需要建立多轴稳定平台在惯性系中的等效运动学模型,以达到在惯性系中真实模拟非惯性系中各项性能指标的目的,为车载试验及应用奠定基础。
1 公路检测用多轴稳定平台
1.1 应用需求分析
当机器视觉应用于公路隧道时,由于内部光照强度有限,数字相机对被测物的适应度降低。同时,隧道尺寸、行车轨迹、外界多轴扰动都将导致相机拍摄距离变化,造成隧道表面位于数字相机工作距离之外,引起图像模糊甚至无法采集图像[14]。因此,隧道的特殊工况对智能检测装备提出了更为严格的要求。
1.1.1 行车轨迹
为了不影响交通,检测系统在高速公路上运行时,车辆时速应在70~120 km·h-1。车辆在高速行驶过程中,在驾驶员主观意识、周围车流量的影响下,行驶轨迹会不可避免地发生偏移。试验表明,车辆沿车道中心线横向偏移量约为±0.5 m。
1.1.2 隧道结构尺寸
由《公路隧道设计规范》(JTG D70—2004)可知,隧道结构尺寸与路面设计时速有关。路面设计时速有60、80、100、120 km·h-1四种级别,对应影响隧道净高分别为6.74、7.03、7.31、7.72 m,拱顶半径分别为5.14、5.43、5.70、6.12 m。
以设计时速为60 km·h-1和120 km·h-1的隧道为例,当在隧道内相同位置拍摄衬砌表面时,两者相差近1 m。同时,对于单向三车道隧道,其结构尺寸较大,隧道净高一般为9 m左右,拱顶半径为8 m左右,此时拍摄距离相差近2 m。
1.1.3 路面颠簸
与隧道外路面结构不同,隧道内路面为半刚性结构,在长时间的外载荷和温度作用下容易发生变形、隆起,导致车辆在隧道内行驶时颠簸更为明显。这种高频振动扰动不仅影响视觉系统采集精度,还严重影响车载设备运行安全。
1.2 稳定平台机构与坐标系统
在外部扰动作用下,视觉系统与隧道衬砌表面的相对位置发生变化,将导致数字相机、光源等设备与被测物的距离和姿态超出设计范围。因此,为了保证图像采集精度,在车辆底盘与视觉系统之间增加一套多轴稳定平台系统,用以隔离车辆多维扰动对视觉系统的影响,如图1(a)所示。考虑到需要隔离车辆空间多维扰动,且视觉系统重量大、车内安装空间有限,因此采用经典的六自由度Stewart机构作为多轴稳定平台的本体结构。
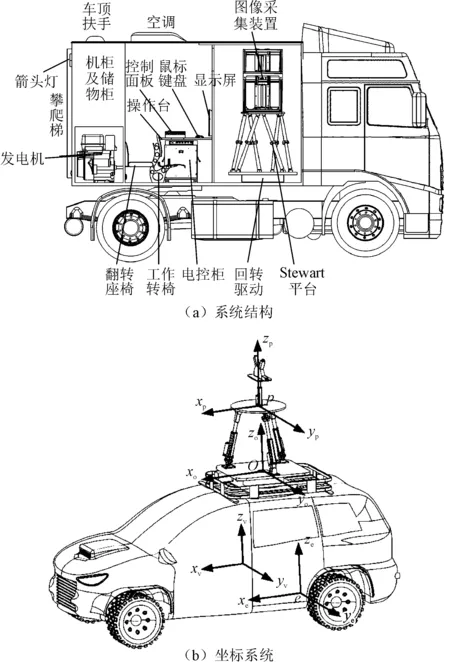
图1 多轴稳定平台系统
为后续研究方便,建立如图1(b)所示的坐标系统:惯性系{e},坐标系原点固连于车辆中心,xe轴沿车辆行驶方向,ze轴垂直底盘向上;车辆坐标系{v},坐标系原点与车辆多维扰动中心重合,当车辆静止时,{v}系与{e}系重合;并联机构定平台坐标系{o},坐标系原点与定平台重心重合,xo轴为车辆行驶方向、yo轴垂直于隧道表面、zo轴垂直向上;并联机构动平台坐标系{p},坐标系原点与动平台重心重合。
受外部扰动作用,车辆在行驶过程中会发生空间多自由度运动,因此在上述坐标系中{v}系和{o}系均为非惯性系。稳定平台用并联机构是一个处于非惯性系中运动的空间复杂多刚体系统,因此其运动学建模方法与传统的建模方面并不相同。
2 多轴稳定平台在非惯性系中的运动学建模
2.1 动平台输出与外部扰动间的数学关系

因此,动平台位姿与外部扰动位姿之间的数学关系为
(1)
式中:Tvo为定平台相对于车辆的位置矩阵,可由并联机构安装位置确定;Tep、Tev分别为定平台、车辆相对于地面的位置态矩阵,可由惯性导航系统测量的参数确定。
利用传统运动描述方法建立复杂多刚体的运动模型时,推导过程复杂;而基于旋量的刚体描述方法具有坐标不变性,可获得较为简洁的数学表达式。由李群理论可知,动平台速度旋量、加速度旋量与其传统速度、加速度之间的关系为
(2)

(3)

(4)
根据式(3)、(4),得到动平台速度与外部扰动速度之间的数学关系即
(5)

同理,建立动平台加速度与外部扰动运动之间的数学关系为
(6)

式中:Θ是一个元素为单位列矢量的反对称矩阵。
2.2 运动分支输入与动平台输出间的数学关系
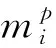
(7)
根据螺旋理论法,可建立运动分支输入速度、加速度与动平台速度旋量、加速度旋量之间的映射关系,即
(8)
式中:G、H为并联机构雅克比矩阵和李括弧雅克比矩阵。
结合式(5)和式(8)建立运动分支输入速度与动平台输出之间的数学关系即
(9)

结合式(6)、(8)建立运动分支输入加速度与动平台输出之间的数学关系即
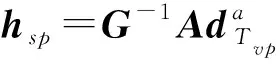
上式进一步整理并化简为
(10)
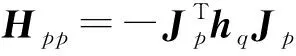
3 数值计算与虚拟样机仿真
3.1 系统参数
以隧道智能检测车为研究对象,设计Stewart机构参数如下:动平台运动副中心点外接圆直径d1=1 600 mm,夹角θ1=10°;定平台运动副中心点外接圆直径d2=1 800 mm,夹角θ2=10°;机构初始高度h=1 200 mm。
为了简化研究过程,使用正弦波模拟车辆扰动,同时在前期研究中发现,车辆侧倾、横移、升降运动对车载仪器采集精度影响较为严重,因此设定车辆相对于大地的运动规律为
(11)
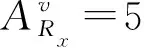
为了给出更一般性的结论,并联机构的动平台相对大地仍然有相对运动量,结合数字相机、激光光源对安装环境稳定性能的要求,设定动平台相对于 大地的六维运动规律仍为正弦规律,对应的三轴转动参数有幅值1°、周期5.9 s;三轴移动参数有幅值10 mm、周期4.2 s。
3.2 仿真与数值计算
结合制定的系统参数及建立的多轴稳定平台在非惯性系中的运动学模型,获得运动分支输入位移、速度、加速度曲线,如图2所示。
在动力学仿真软件中建立稳定平台系统的虚拟样机模型,并在并联机构动平台及车辆质心中添加多轴虚拟驱动。将上节中的运动规律作为样条曲线输入到多轴驱动上进行运动学仿真。多轴稳定平台虚拟样机按照上述规律运动后,通过动力学仿真软件测量各运动分支处的相对位移、速度、加速度,如图3所示。对比图2、3中对应的曲线,两者变化趋势及幅值完全相同,这也验证了本文理论分析方法的正确性。
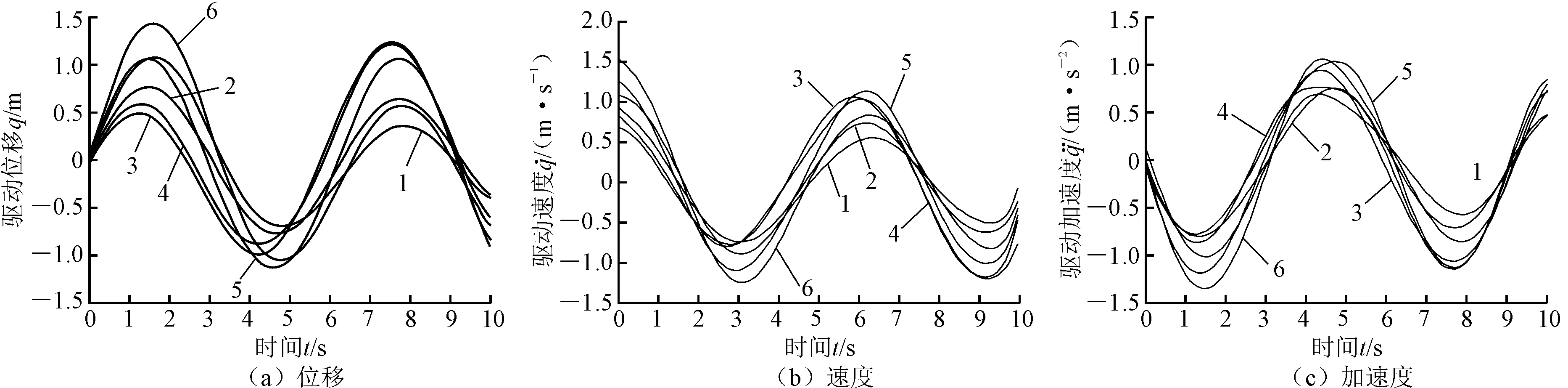
图2 数值计算结果

图3 虚拟样机仿真结果
4 运动学模型在惯性系中的等效变换
4.1 等效运动参数
车辆、动平台按给定规律运动时,按式(1)建立了动平台运动参数ψx、ψy、ψz、Sx、Sy、Sz与车辆扰动、动平台主动运动之间的表达式,采用10次样条差值函数建立动平台相对于定平台的位姿数学表达式即
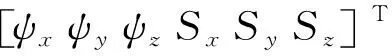
(12)
式中:μ代表各元素值,如表1所示。
若并联机构定平台与大地固连,即多轴稳定平台处于惯性坐标系中,此时定平台坐标系{o}为惯性系。定平台按式(12)所述的位姿参数相对{o}系运动,本文将这一过程称为多轴稳定平台机构由非惯性系到惯性系的等效变换,相应的数学模型称为等效运动学模型。
4.2 所处坐标系对运动学性能的影响
结合式(12)及多刚体系统运动旋量之间的数学关系,建立t时刻动平台在惯性系中等效速度、加速度旋量分别为
(13)
(14)
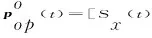
由于多轴稳定平台在非惯性系和惯性系中的运 动学参数完全相同,因此根据等效运动参数(表1)获得的运动分支位移与稳定平台在非惯性系中获得的结果完全相同。依据并联机构末端输出与分支输入速度、加速度的映射关系,在等效运动参数作用下,当稳定平台处于惯性系中运动时,运动分支输入速度、加速度数学表达式为
(15)
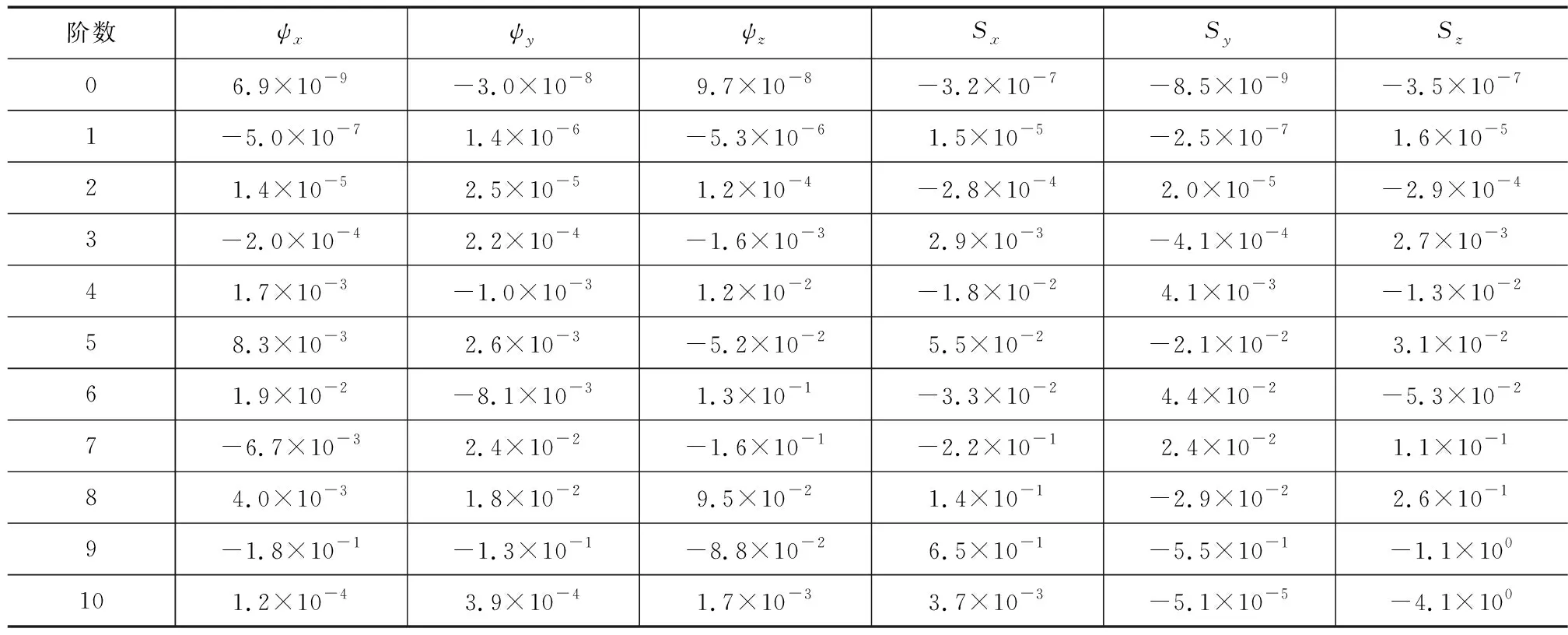
表1 动平台等效运动参数
4.3 数值分析
当多轴稳定平台的动平台按等效运动参数运动时,结合式(13)~(15),获得运动分支速度、加速度变化曲线,如图4所示。与图2对应曲线相比,各运动分支曲线在中间时间段完全相同,但是在开始和结束时刻不完全一致。造成上述现象的原因是,动平台位姿函数是由各离散数据点拟合而成,因此在初始及结束阶段样条曲线的差值精度较差。当分析速度、加速度时,需要获得位置曲线的一、二阶时间导数,此时这种拟合误差将会被放大,因此由计算获得运动分支速度曲线在两端误差并不大,而加速度曲线与非惯性系模型相比差距较大。
5 结 语
(1)基于并联机构的多轴稳定平台可用于补偿车载外部扰动对视觉系统的影响,实现车载设备相对惯性空间稳定,提高设备工作精度。
(2)基于李群李代数建立的并联机构在非惯性系中的运动学模型,具有形式统一、推导过程简单、坐标不变性等优点,仿真结果验证了理论建模的正确性,该建模方法可应用于复杂多刚体的动力学问题。
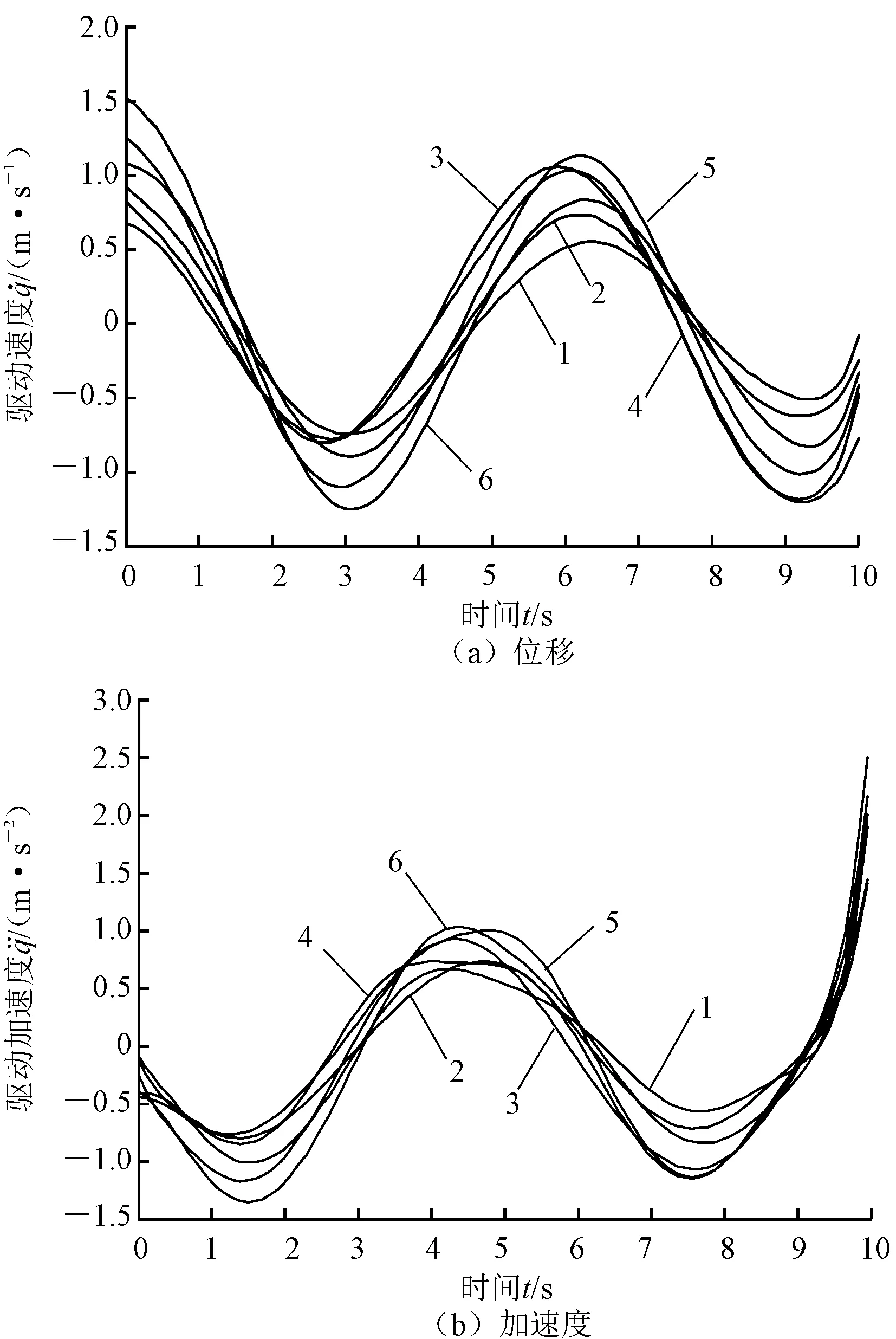
图4 等效运动学模型下的运动分支输入量
(3)并联机构在非惯性系和惯性系中的运动学建模并不完全相同,机构所处坐标系对其运动学性能影响较大。
(4)通过运动参数等效变换建立了机构在惯性系中的等效运动学模型,数值分析结果表明,提出的运动学模型等效变换能够完全模拟车载稳定平台在实际中的各项性能指标,为下一步开展地面试验提供了理论依据。
