单轴压缩作用下混凝土全场应变分析方法研究

2018-09-01刘翌晨杨家琦

水利科技与经济 2018年3期

刘翌晨，杨家琦，李琦

(河北工程大学水利水电学院，河北邯郸 056038)

0 引言

混凝土是建筑材料的重要组成部分。由于现有工程设施的老化及新工程的施工，对混凝土应变的监测、评估及分析显得愈发重要。数字散斑相关方法(Digital Speckle Correlation Method，DSCM)作为一种应变的测量方法，在全场应变测量时兼具准确性和高效性[1]。但其也有仪器成本较高，易受外界光源干扰的缺点。采用数值模拟方法对混凝土全场应变进行分析，不但能降低试验成本，而且能进行多次重复试验提高结果精度。二维颗粒离散元PFC2D作为Itasca公司在Cundall和Strack提出的离散元法[2]的基础发展而成的商业软件，其在模拟过程中通过对介质内部结构的分析来获得整个介质系统力学特征的分析方法，与混凝土试样本身为不连续的颗粒介质的特性恰好吻合；在微观上的裂纹模拟，也可以有效地对混凝土的力学特性进行模拟研究[3]。目前，国内外学者已经对混凝土的离散元模型进行了许多研究，取得了一些成果。例如，Potyondy和Cundall[4]将黏结模型引入离散元，为连续固体的离散元模拟提供了基础；王云飞[5]等对混凝土单轴压缩过程中粗骨料的影响进行了分析；Qin[6]等基于二维细观离散元模型分析了碱骨料反应对混凝土单轴受压力学性能的劣化影响。但是，之前的数值模拟大多从应变平均量进行分析，而未综合考虑试样整个区域内的应变状态。本研究中使用数字散斑相关方法对试样全场应变进行测量，之后使用二维颗粒离散元程序PFC2D对压缩试验过程进行数值模拟，并生成全场的应变云图。将物理实验与数值模拟所得结果进行对比分析，探究混凝土单轴受压过程中的全场应变变化规律。

1 试验概况

1.1 试验原材料及配合比设计

本试验使用的混凝土是一种无砂型的水泥(粉煤灰)-煤矸石凝膏体，它的构成包括水泥、粉煤灰、煤矸石骨料和水。该混凝土材料配置如下：水泥采用标准的42.5普通硅酸盐水泥，煤矸石骨料原材料取自邯郸市陶一矿，粉煤灰原材料取自邯郸地区热电厂，拌和用水为自来水。具体配合比见表1。

表1 混凝土配合比表 /kg·(m3)-1

注：表1中水灰比实际是水与水泥和粉煤灰总和的单位体积重量之比。

根据研究设备的要求，按照表1中配比，采用搅拌机制作150 mm×150 mm×150 mm试样9个，在养护箱中50℃分别养护3、7和28天。

1.2 实验装置

本实验采用的加载装置为TAW—2000电液伺服岩石三轴试验仪。该系统采用微机控制加载速率，可实时记录当前应力、位移的大小，并可将荷载-位移、应力-时间等曲线实时可视化显示。试验采用的是轴向位移控制，加载速率为0.2 mm/min。

1.3 VIC-3D原理及系统配置

数字散斑相关方法是一种基于数字图像处理和数值计算的全场变形测量技术[7,8]。其主要测量过程为：首先选定变形过程中具有灰度值图案的较小邻域，我们称之为subset(子区)。找出该子区的前后对应关系，就可以实现对该区域变形量的获取。在寻找样本子区与变形后子区对应关系的过程中，引入函数C对其相关程度进行评价[9]，具体计算方法如下：

(1)

采用Newton- Rapshon非线性方法对式(1)进行极值求解，即可得到前后的变形量[10,11]。进而对邻域内散斑图像的相对位移进行求解，计算出物体表面位移及应变分布。用这种方法对参考图像中的其余多个像素点进行相关计算，即可得到该计算区域的位移场[12]。

试验前，在试件表面均匀喷涂白色喷漆，等待喷漆变干后使用黑色油漆笔于试样表面进行随机散斑处理。考虑到摄像机拍摄散斑的清晰度及数据处理的便捷度，散斑的直径须大于2 mm。建立坐标系，水平方向为X轴，竖直方向为Y轴。试验时，先对摄像机进行校准及调零，获得采集过程中所需的参数。在试验过程中，为了保证采集信息的完整，要尽量避免外界自然光的干扰。

图1 随机散斑处理后的试样及VIC-3D设备实验装置

2 物理实验结果及分析

整理VIC-3D系统在煤矸石混凝土单轴压缩过程中所采集到的资料，在立方体试块朝仪器面图像中心点位置选择分析区域AOI为120 mm进行分析，考虑试样变化明显程度，选取7天时特征最明显的3号试样。图2为混凝土试样在加载过程中的应力～应变变化曲线，图3中图像为曲线上O、A、B、C点对应的应变云图及试样的最终破裂图像，将应力～应变曲线与图像结合，共同作为分析试样单轴压缩过程中应变特征的参考依据。

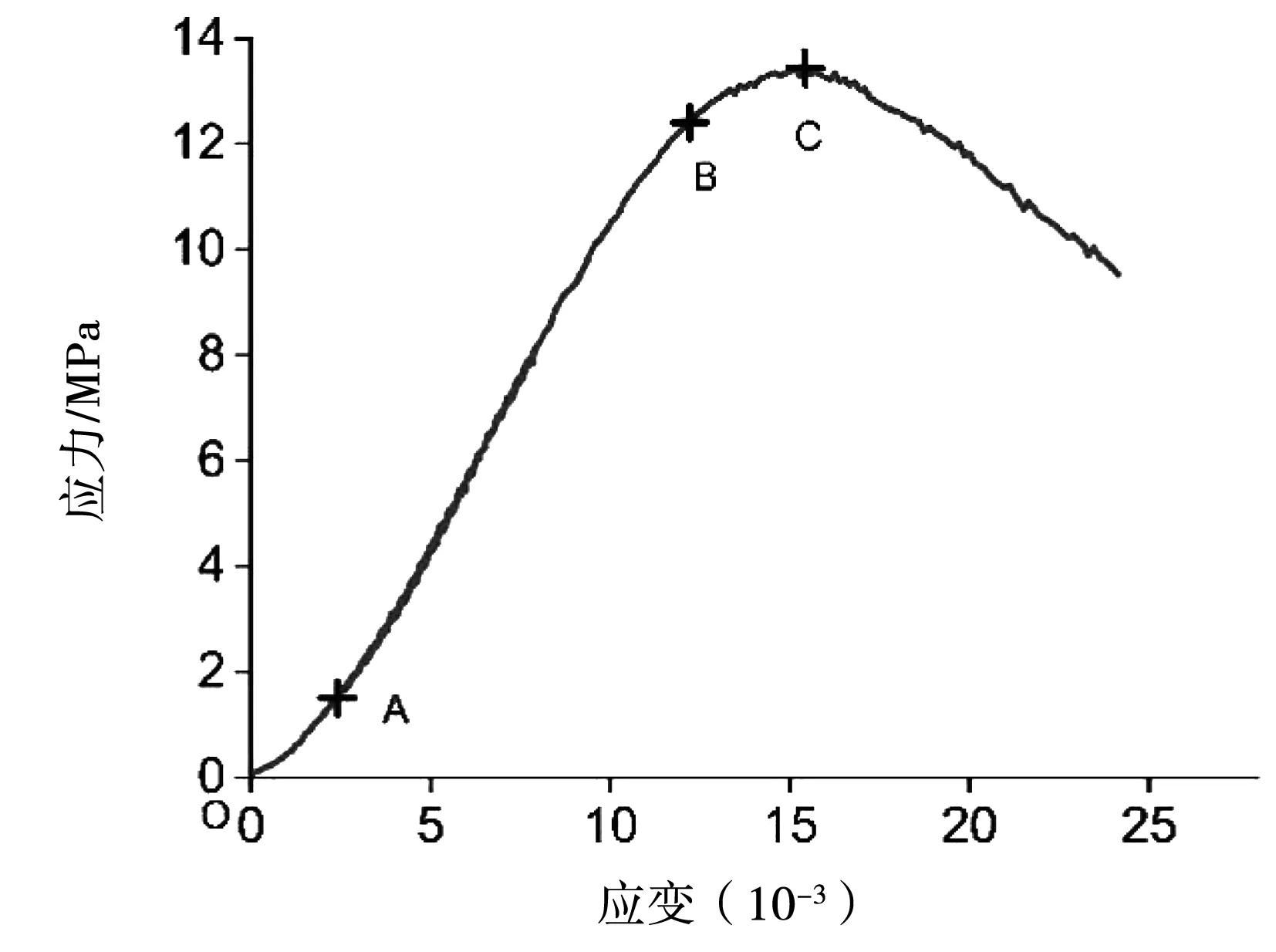
图2 单轴压缩应力～应变曲线

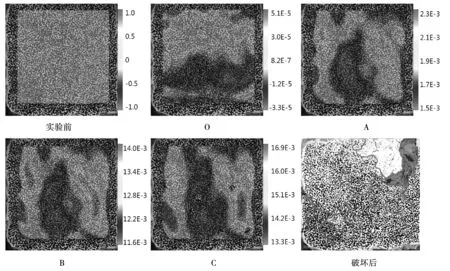
图3 特征点应变云图及破坏后图像

观察应力应变曲线，将试样变形破坏分为5个主要阶段：① 试验前阶段。该阶段VIC-3D设备在经过调零后，所采集到的图像颜色出现暂时的均一稳定状态，图像中没有明显“色差”(即应变几乎没有波动)。表明试样在测量前受到外界环境(主要影响因素为外界光照)的影响较小且外界环境相对稳定。② OA段(密实阶段)。该阶段为试样加载初期，曲线斜率较小。在加载过程中，内部孔隙和微裂隙逐渐被压至闭合，与此同时，局部区域发生微破裂。O点处为加载的瞬时，整体应变数值和后续相比要低2～3个数量级。此时可以明显观察到试样上方部分出现应变集中现象，但整体应变分布无明显规律，应该是试样内部不均匀导致应变较为离散。③ AB段(弹性变形阶段)。该阶段试样的应力应变关系呈线弹性关系，应力～应变曲线接近直线，应变场稳定波动。在过渡点A处，应变大体呈现两侧大中间小的趋势，左下方部分区域“颜色”较深，可能由于该位置粒径较大，产生应变集中。在B处，应变值增大，但试样整体应变分布规律与A处接近。④ BC段(塑性变形阶段)。应力～应变曲线的斜率逐渐减小，试样内部逐渐产生大量微裂纹。在C点处应变云图表面有部分小区域信息缺失，实时观察到在试样表面该部分有细小裂纹产生，应该是在裂纹产生后试样表面翘曲产生反光导致该点的信息缺失。⑤ CD段(破坏阶段)。在试样达到峰值强度后，试样发生失稳破坏，应力～应变曲线迅速下降，试样内部裂隙不断向外扩展延伸，在表面产生明显的宏观裂缝。在D点，试样已经完全破坏，应变图上出现大量信息缺失，可以明显观察到裂缝走向。

3 数值模拟研究

3.1 模型建立

参照物理模型，在PFC2D中生成150 mm×150 mm的试样。为了对试样边界进行控制，首先使用fish语言生成150 mm×150 mm的墙体，采用式(2)预计算在区域内要生成的颗粒数。

(2)

式中：b、h分别是模型的宽和高；n2是模型的孔隙率；r为颗粒半径；[N]代表对数字N向下取整。

由式(1)预求得模型颗粒数为9 404，在墙体内部使用半径扩大法在边界内部生成颗粒。由于在PFC中无法直接设置各种宏细观参数间的对应关系，需要根据物理实验中所得的抗压强度、弹性模量等宏观力学参数来对细观参数反复调整，使二者相互匹配。具体细观力学参数见表2。

表2 细观力学参数

在采用表2中细观参数的情况下，设置轴向加载速率为0.02 m/s，完成整个加载过程，得到单轴压缩过程中的应力～应变曲线，并与实际试验所得应力～应变曲线进行对比，见图4。从图4可以看出，不同于物理试验的非线性变化，模拟所得的应力随应变发展基本呈线性增长。这是由于物理试验中混凝土内部颗粒的尺寸不规则及分布不均匀，而在细观尺度的模拟中较难实现这一现象所导致的。但模拟所得单轴峰值强度、弹性模量分别为13.2 MPa和0.015，与物理实验所得单轴峰值强度、弹性模量13.4 MPa和0.015基本一致，且数值模拟与物理试验具有相似的宏观破坏裂纹和应变云图。因此，采用表2中细观参数模拟的本次单轴压缩试验可以较准确地反映混凝土试样的力学性质。

采取所选细观参数建立模型后，选取与物理试验相同的应变监测区域120 mm。综合考虑结果精度与计算复杂程度，选取1 000个监测圆对区域内应变进行监测，监测圆直径为15 mm，圆心均位于监测区域内部。在获得监测圆内信息后，将所监测值填充到监测点附近区域，最后采用3次样条插值对整个监测区域进行插值计算，得出区域内应变云图。

图4 模拟与实际应力～应变曲线及裂纹数目曲线

3.2 数值模拟分析

模拟位移云图见图5。对照图4可知，在OA段，试样处于压密阶段。但由于前文所述模拟过程中应力随应变呈线性增长，所模拟的应变云图整体趋势已经呈现，即两侧应变较大，中心应变较小。在此过程中，模拟试样内裂纹数始终为零，试样未出现裂纹。AB段为弹性阶段，此段试样两侧应变继续迅速增长，左侧有与物理试验类似的小区域应变高度集中。AB间F点(First crack)应变为5.16×10-3时监测到混凝土试样的第一条裂纹出现，此后微裂纹数目暂时缓慢增长，模拟试样表面未出现明显变化。B点后，裂纹数目发生陡增，试样进入塑性变形阶段。裂纹的迅速增长使得试样表面产生连贯裂缝。到达C点，试样达到峰值强度。此时裂纹数为853条，由于裂纹的产生，试样内部分颗粒相较于原位置已经产生较大变化，其应变量也相对较大，在差值计算后整个模型应变量较大，但仍然可以看出试样应变分布的趋势，即两侧较大，中间较小。C点后，试样破坏，各颗粒位移量高速提升；试样间裂纹数迅速增长。在强度跌落到峰值强度的50%，即应力再次小于6.7 MPa后，模拟停止。整个模拟过程与物理试验采集到的应变信息基本相符，试样受载过程中的裂纹变化也与破坏过程较好地吻合，验证了此模型对无砂混凝土单轴受压过程的应变分析是有效的。