不同支撑形式的型钢混凝土剪力墙抗震性能试验研究
2018-08-31王玉镯高希虎许德建王慧敏傅传国
王玉镯,高希虎,许德建,王慧敏,傅传国
(1.山东建筑大学 土木工程学院,济南 250101;2.山东职业学院 铁道工程与土木工程系,济南 250104)
高层建筑在现代建筑中占据越来越重要的地位,其结构安全受到越来越广泛的关注,各种灾害中,地震作用对建筑物的危害尤为严重。目前,高层建筑普遍采用剪力墙作为结构的核心抗侧力构件,传统剪力墙在力学性能方面虽然能够满足结构的基本要求,但因其延性性能较差,发生地震时极易发生脆性破坏,有待进一步改进。在普通剪力墙中加入不同形式的型钢支撑来提高墙体结构的力学性能,得到一种新型剪力墙,即型钢混凝土剪力墙。

已有研究成果主要集中在钢板混凝土剪力墙、带钢桁架或X型支撑钢骨剪力墙方面,大多仅是对X型支撑剪力墙进行试验研究,而没有将不同支撑形式进行对比分析。笔者通过考虑不同型钢支撑形式对剪力墙抗震性能的影响,以确定最优的型钢支撑布置形式,进行了3个不同支撑形式(均采用工字钢)型钢混凝土剪力墙和1个普通混凝土剪力墙对比试件在低周反复荷载作用下关于抗震性能的试验研究。
1 试件概况
1.1 试件设计
试验共设计了4个试件,其中3个带型钢支撑的剪力墙试件(SW-X1、SW-P1-、SW-R)和1个普通剪力墙对比试件SW-D,其截面形式全部是矩形(宽800 mm,厚200 mm),混凝土采用C40的商品混凝土,分布筋和主筋均采用HRB400热轧带肋钢筋,拉筋采用φ6.5的光圆钢筋,支撑形式分别为:X型(SW-X1)、AC1型(SW-P1)和AC2型(SW-R),如图1所示。剪力墙详细参数及配筋见图2和表1。
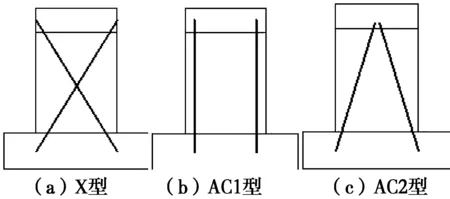
图1 不同型钢支撑示意图Fig.1 Diagram of different types of steel
X型支撑,布置相对复杂,工字钢在墙体中对角布置,两型钢交叉处焊接,形成一个整体,可有效提高剪力墙试件的水平抗侧力;AC1型,两工字钢平行布置于墙体两侧,可有效提高试件水平抗侧力的同时,较X型支撑布置简单;AC2型,工字钢下端靠近墙体两侧边缘,上端靠近墙体中心位置,斜向布置,其倾斜度小于X型支撑,大于AC1型支撑,是介于X型与AC1型之间的支撑形式。通过研究3种不同型钢支撑形式下型钢混凝土剪力墙试件的抗震性能,寻求最佳支撑类型。
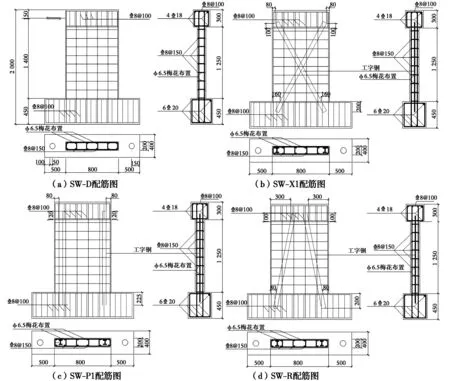
图2 试件配筋图Fig. 2 Reinforcement layout of
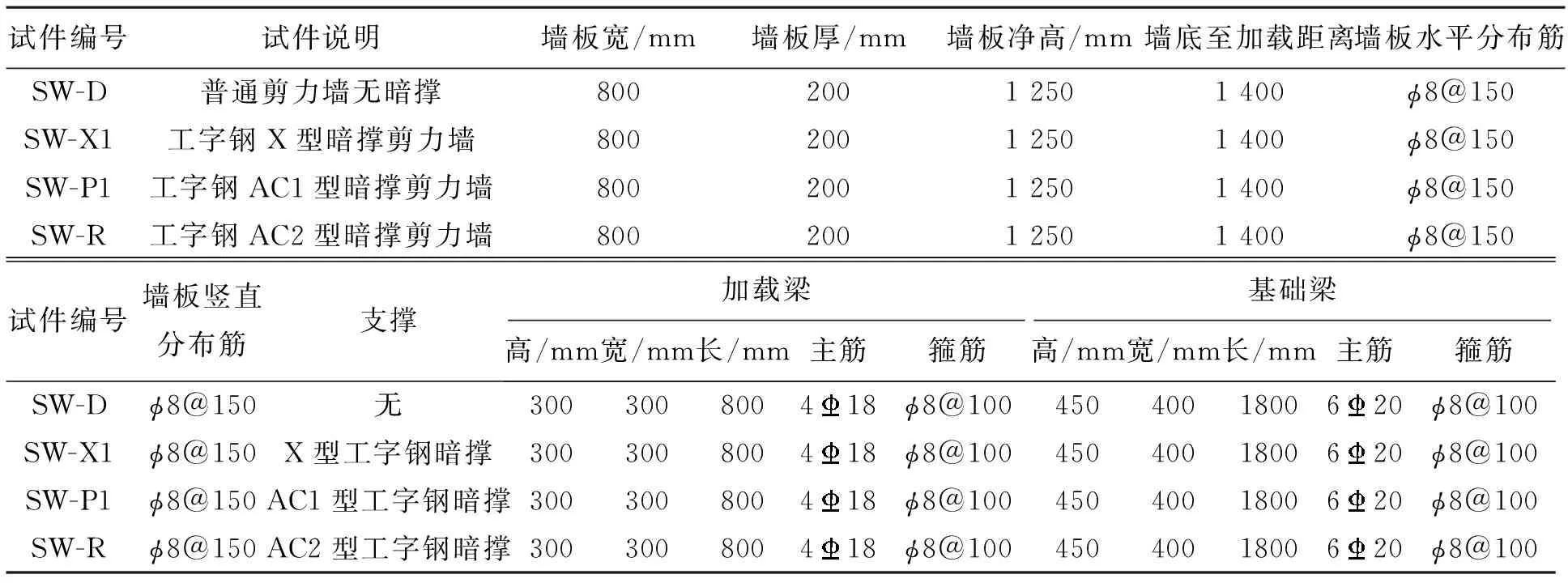
试件编号试件说明墙板宽/mm墙板厚/mm墙板净高/mm墙底至加载距离墙板水平分布筋SW-D普通剪力墙无暗撑8002001 2501 400ϕ8@150SW-X1工字钢X型暗撑剪力墙8002001 2501 400ϕ8@150SW-P1工字钢AC1型暗撑剪力墙8002001 2501 400ϕ8@150SW-R工字钢AC2型暗撑剪力墙8002001 2501 400ϕ8@150试件编号墙板竖直分布筋支撑加载梁高/mm宽/mm长/mm主筋箍筋基础梁高/mm宽/mm长/mm主筋箍筋SW-Dϕ8@150无300300800418ϕ8@1004504001800620ϕ8@100SW-X1ϕ8@150X型工字钢暗撑300300800418ϕ8@1004504001800620ϕ8@100SW-P1ϕ8@150AC1型工字钢暗撑300300800418ϕ8@1004504001800620ϕ8@100SW-Rϕ8@150AC2型工字钢暗撑300300800418ϕ8@1004504001800620ϕ8@100
1.2 材料的力学性能
在试件的制作过程中,采用同批混凝土制作了一组立方体试块(共3块),在现场同等条件下养护28 d,然后进行测试,结果见表2。同时,对试验中用到的钢筋和型钢进行材料性能试验,试验结果详见表3和表4。

表2 混凝土的力学性能指标Table 2 Mechanical properties of concrete
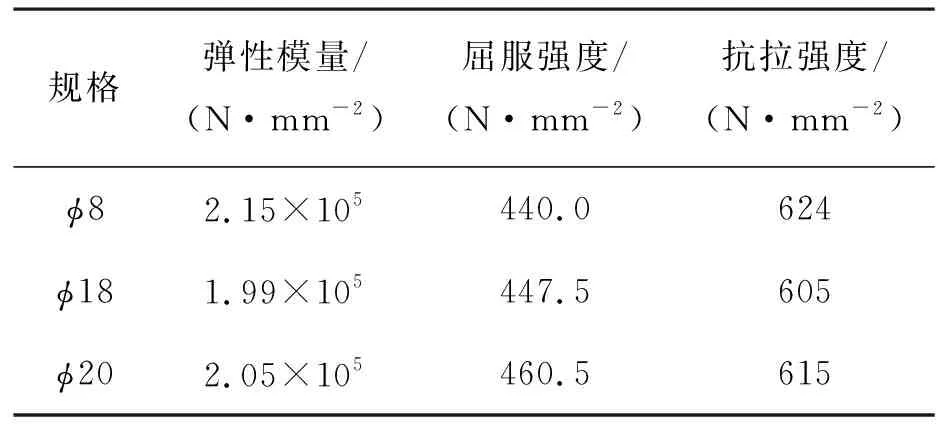
表3 钢筋的力学性能指标Table 3 Mechanical properties of reinforcing bars

表4 型钢的力学性能指标Table 4 Mechanical properties of steel
2 试验概况
2.1 加载装置
试验加载方式如图3所示,使用1 000 kN MTS对剪力墙作用反复水平荷载,同时使用固定在门式反力架上的千斤顶对试件作用竖向恒定荷载。通过地锚螺栓将剪力墙固定于试验室地面,作动器固定于反力墙上,并与剪力墙通过水平链接扣件紧密连接。
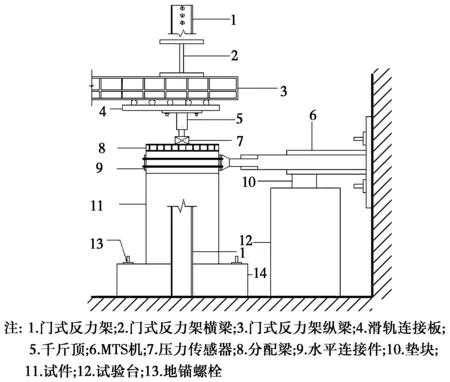
图3 加载装置图
2.2 加载制度
竖向荷载:试验开始前,通过分配梁将竖向荷载P=550 kN(轴压比为0.13)作用于剪力墙上,并且在整个加载过程保持不变。
水平荷载:为模拟地震作用下试件受力过程,在距离基础梁上顶面1 400 mm处使用MTS作用反复水平荷载。该试验整个加载过程采取位移控制,步长全部采用2 mm,每一级位移往复两次,加载制度见图4。当试件不能继续保持竖向荷载值稳定或者水平荷载降到最大荷载的85%,试验终止。
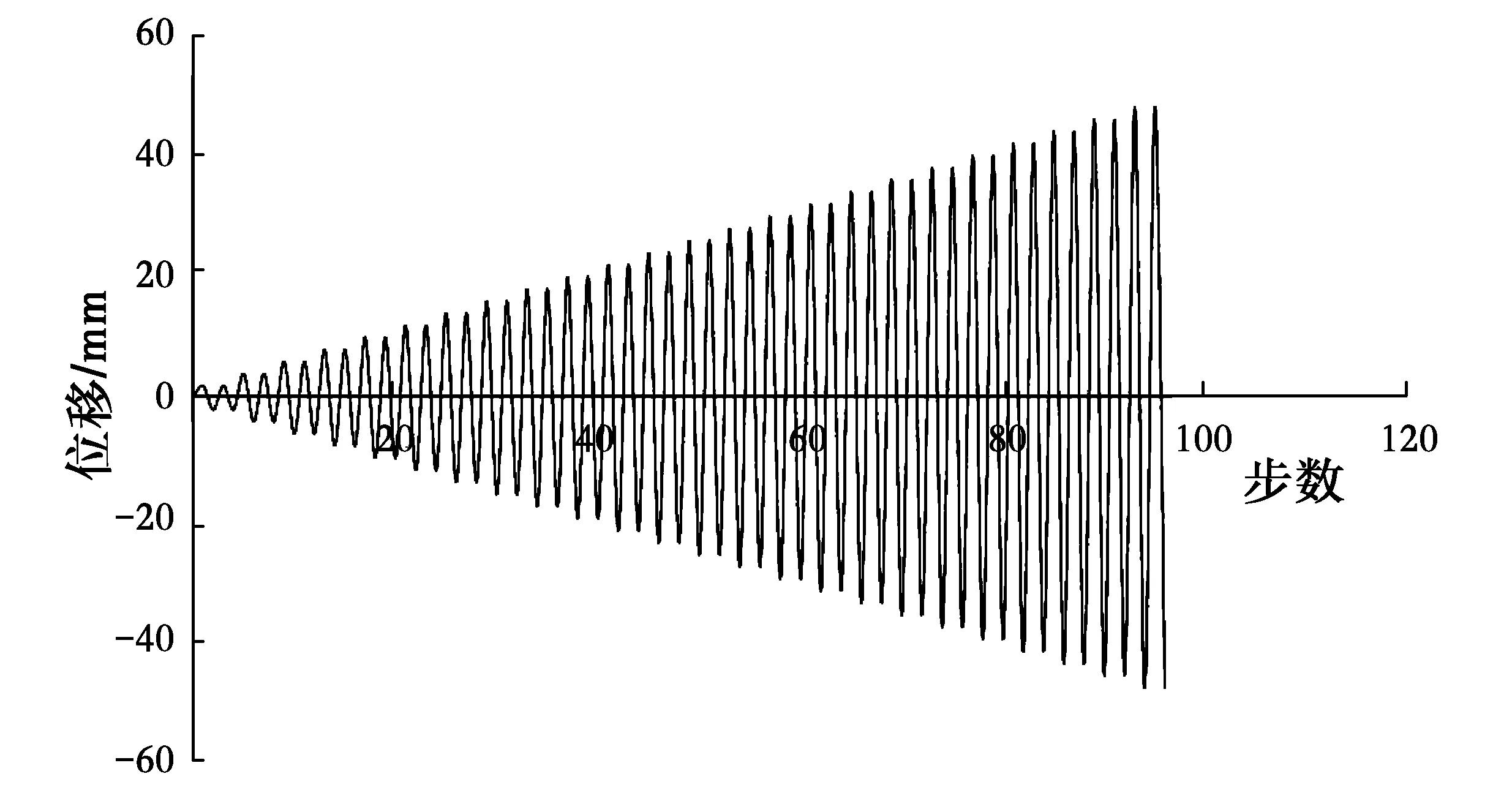
图4 加载制度示意图
2.3 观测内容
试验中量测了试件的荷载、位移和应变。水平荷载与位移均由MTS伺服液压加载系统测量与记录,竖向荷载采用压力传感器测量。应变测量包括墙体两侧混凝土、墙中水平分布筋、墙中竖向分布筋和型钢支撑的应变,各试件中应变片布置如图5所示。试件的裂缝开展和最终破坏情况采用手工描缝和数码相机拍照记录。
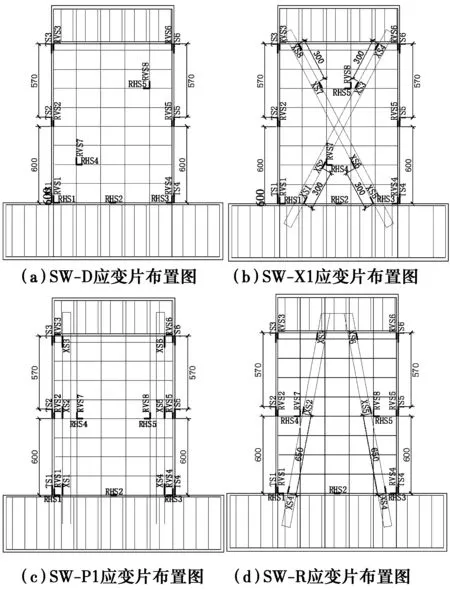
图5 试件应变片布置图Fig.5 Arrangement of strain
3 试验现象分析
3.1 试件SW-D
当位移步Δ=+6 mm时,在试件A端距底部33 cm处出现第一道细微的水平裂缝。当位移步Δ=-6 mm时,试件B端距底部约33 cm处出现一道新的水平裂缝,原有裂缝的端部产生微裂缝。之后随位移逐渐增加,裂缝继续开展,并向斜下方延伸,两条主裂缝交汇。当位移步Δ=+24 mm时,原有裂缝持续发展,底部边缘有竖向微裂缝出现,B端底部出现混凝土剥落。位移步Δ=+28 mm后,试件两端底部破坏严重,水平荷载降至其最大荷载的85%,试验终止。破坏现象如图6所示。

图6 试件SW-D破坏图
3.2 试件SW-X1
当位移步Δ=+6 mm时,在试件A端距底部约48 cm处产生第一道水平裂缝。当位移步Δ=-6 mm时,在试件B端距底部约30 cm位置处呈现出一条新裂缝,呈水平状微向下倾斜。当位移步Δ=+10 mm时,A端距底部48 cm处的裂缝继续向墙身内扩展,并且距底部5 cm位置处发现新裂缝,斜向下发展,过程中伴有“噌噌”声。在位移步Δ=+16 mm时,在A端距底部78 cm位置处有两道新的水平短裂缝。当位移步Δ=-16 mm时,B端距底部30 cm处的裂缝与A端裂缝贯通。随着位移步继续增大,裂缝不断开展,并且出现掉渣现象,剪力墙底角处混凝土开始剥落。在位移步Δ=+42 mm后,剪力墙两端底部混凝土被压碎,发生脱落,水平荷载降至其最大荷载的85%,试验终止。破坏现象如图7所示。

图7 试件SW-X1破坏图
3.3 试件SW-P1
当位移步Δ=+10 mm时,试件A端距底部约28 cm处出现第一道裂缝,呈水平状向内部延伸。当位移步Δ=+12 mm时,在试件A端距底部约33 cm位置处有一道新的水平短裂缝,开展缓慢。当位移步Δ=-12 mm时,在试件B端距底部22 cm位置处产生一道水平裂缝,迅速向墙体中心位置发展。当位移步Δ=+20 mm时,在试件A端距底部约65 cm位置处产生一道新裂缝,沿约45°方向斜向下迅速开展,穿过墙体中心位置。当位移步Δ=+24 mm和-24 mm时,在A端距底部91 cm和B端距底部35 cm处分别出现水平状裂缝,向墙内发展。之后随位移持续增长,裂缝不断开展,试件两侧出现较多斜向短裂缝,剪力墙底角处出现混凝土脱落现象。在位移步达到+52 mm后,剪力墙两端底部破坏,水平荷载降至最大荷载的85%,试验终止。破坏现象如图8所示。

图8 试件SW-P1破坏图
3.4 试件SW-R
当位移步Δ=-8 mm时,试件B端距底部约31 cm处产生第一道裂缝,呈水平状向墙内延伸。当位移步Δ=+12 mm时,试件A端距底部约9 cm处有一道新裂缝,并迅速向墙体中心位置发展。当位移步Δ=+14 mm时,在试件A端距底部34 cm处发现新裂缝,斜向下发展。当位移步Δ=+16 mm时,斜向裂缝在墙体中间位置交汇。当步长Δ=+18 mm时,原有裂缝继续开展,且在端部产生若干微裂缝。随位移步不断增加,陆续出现若干条裂缝,出现位置逐渐增高,原有裂缝继续扩展和延伸。当位移步Δ=+34 mm时,在B端底角处发生混凝土剥落现象。在位移步Δ=+46 mm后,水平荷载降低至其最大荷载的85%,试验终止。破坏现象如图9所示。

图9 试件SW-R破坏图
3.5 试件破坏形态比较分析
通过对上述4个试件破坏形态的对比分析(如图6~图9所示)可以看出:
1)试件SW-X1、SW-P1、SW-R与试件SW-D的破坏模式类似,均为弯剪型破坏。试件裂缝开展之初大多为水平方向,随着位移的增加,逐渐斜向发展,且剪力墙破坏时底角处混凝土出现压碎、剥落现象。
2)对比试件SW-D裂缝较少,且开展较快,斜裂缝为约45°斜向下发展;试件SW-X1裂缝相对试件SW-D增多,且裂缝开展区域高度有所增加,斜裂缝发展方向与型钢支撑布置方向相似,说明支撑的存在可以控制裂缝的发展走向;试件SW-P1裂缝一直延伸至墙身2/3高度处,裂缝发展最充分,且分布范围广;试件SW-R的裂缝以斜裂缝为主,且裂缝主要集中在墙身1/2以下位置。
3)型钢混凝土剪力墙裂缝发展范围均比普通剪力墙显著增加,说明支撑的存在可以有效地增大剪力墙的塑性区高度,其中带AC1型支撑试件SW-P1的裂缝分布范围最广,塑性区最大。
4 试验结果分析
4.1 滞回曲线
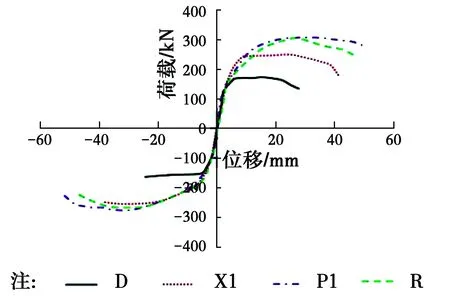
试验采用MTS自动记录每个试件水平荷载与位移的滞回关系曲线,然后以此来分析每个试件的抗震表现。SW-D、SW-X1、SW-P1和SW-R的滞回曲线如图10所示,通过分析比较可知:
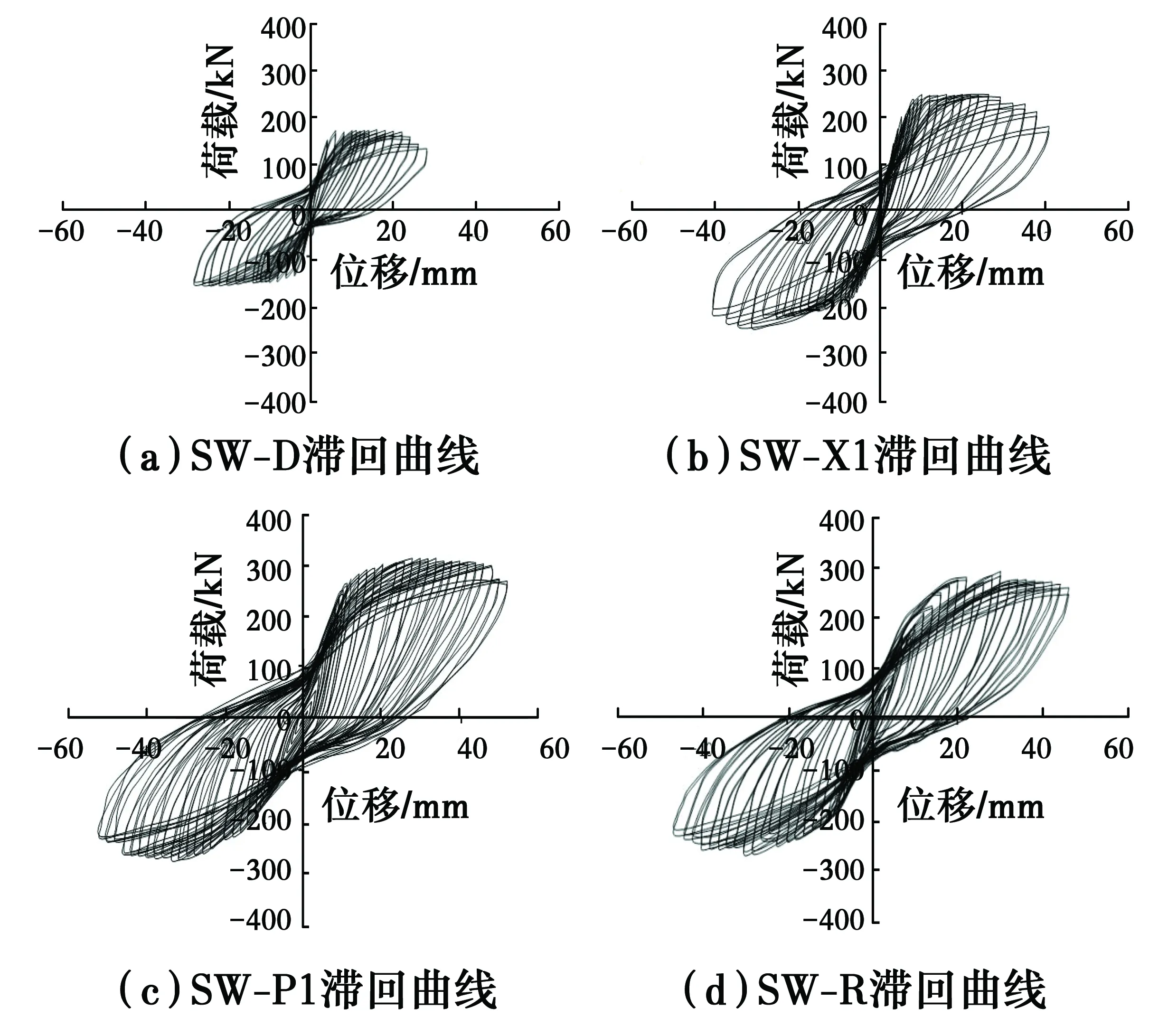
图10 滞回曲线Fig.10 Hysteretic loops of
1)开裂前,各试件均处于弹性工作阶段,此时残余应变很小,滞回环面积也很小;
2)开裂以后到屈服前,水平荷载增长速率下降,滞回曲线斜率随位移的增加而逐渐变小;
3)整体屈服以后,随着位移的增加,塑性变形占总变形的比例不断增大,水平荷载增长随之变缓,达到最大值后水平荷载逐渐降低,但滞回环包络面积还在不断增大,表现出了良好的塑形变形能力;
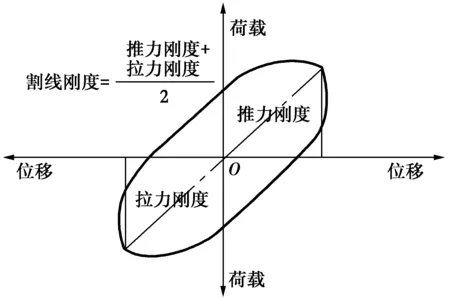
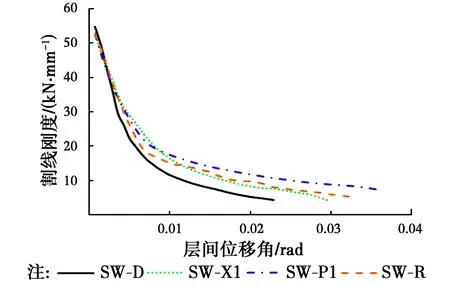
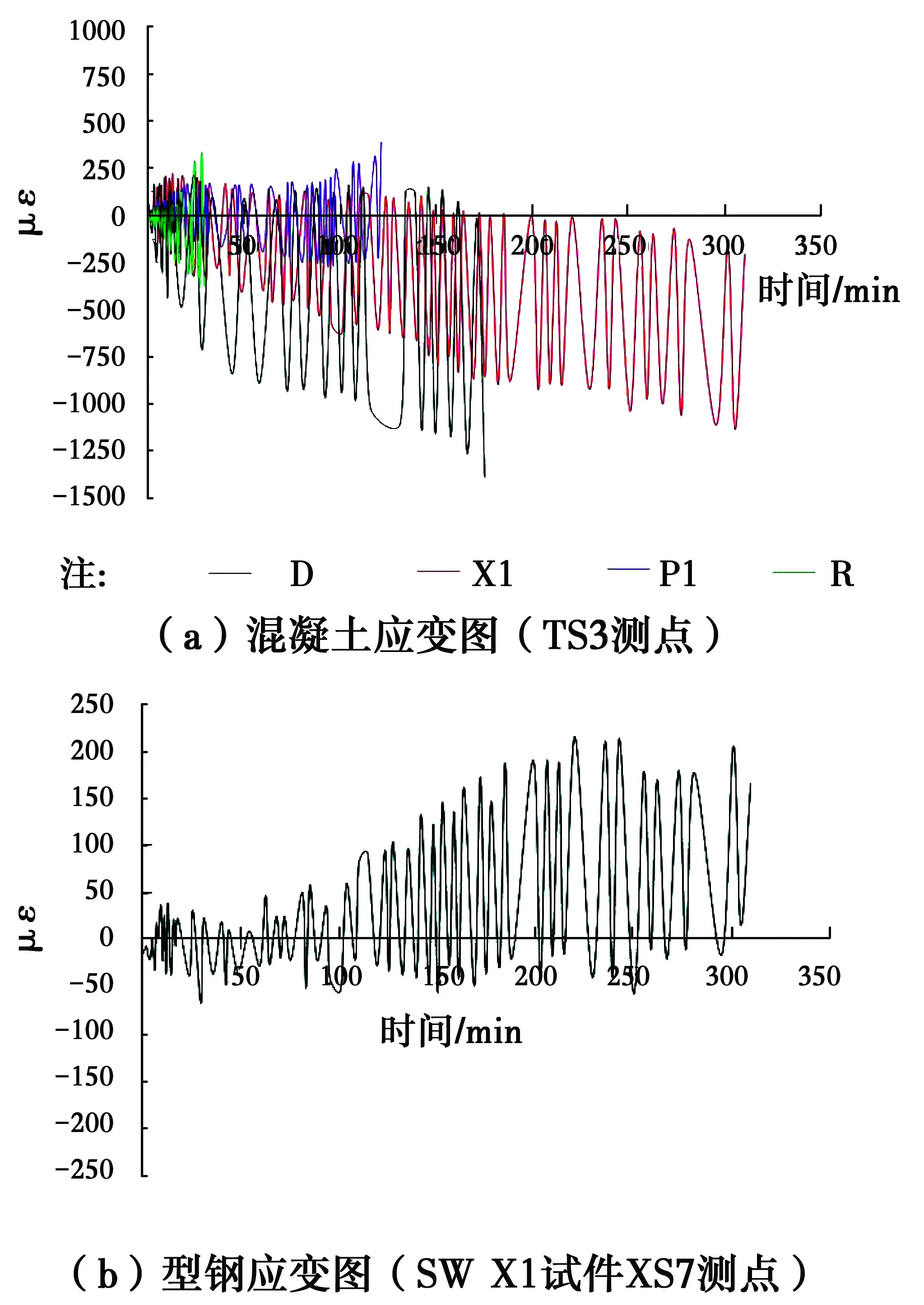
4)从图10可以看出,滞回环面积:SD 图11 荷载位移骨架曲线Fig.11 Skeleton curves of 骨架曲线作为研究结构构件非线性性能的重要数据,为研究结构构件在地震作用下的弹塑性性能提供了基础依据。比较图11中4条骨架曲线,可以发现:在弹性工作阶段,试件的初始刚度大致相同;裂缝出现以后,刚度开始下降,带支撑试件承载能力明显大于对比试件,支撑形成的核心束可以约束裂缝开展;随着位移的增加,骨架曲线的斜率随之下降,对比试件水平荷载增长非常缓慢,带支撑试件中由于型钢支撑的作用骨架曲线斜率明显大于对比试件,且荷载值也明显大于对比试件;在达到最大荷载之后,SW-D的骨架曲线下降段比较陡,承载力衰减很快,SW-X1、SW-P1和SW-R骨架曲线下降段则较为平缓,承载力下降相对缓慢,说明支撑的存在可以减缓后期试件的破坏,提高了试件后期的抗震性能。 各试件开裂荷载、屈服荷载和极限荷载如表5所示。 表5试件的开裂荷载、屈服荷载和极限荷载 编号正向加载Fc/kNFy/kNFu/kN负向加载Fc/kNFy/kNFu/kN均值Fc/kNFy/kNFu/kN强屈比Fu/FySW-D158.51167.34173.74149.00155.50164.57153.76161.42169.161.05SW-X1202.84245.33247.54176.14210.67257.82189.49228.00252.681.11SW-P1223.46245.58308.40183.81224.04274.81203.64234.81291.611.24SW-R206.50235.83289.90180.52215.84266.95193.51225.84278.431.23 注:Fc为试件的开裂荷载,Fy为试件的屈服荷载,Fu为试件的极限荷载,极限荷载与屈服荷载的比值Fu/Fy为试件的强屈比。 由表5中的试验数据可以发现: 1)带型钢支撑试件的屈服荷载和极限荷载比对比试件都有很大提升,说明型钢支撑的布置能够有效提高试件的承载力,试件SW-X1、SW-P1和SW-R的屈服荷载分别提高了41.2%、45.5%和39.9%,极限荷载提高了49.4%、71.9%和64.6%,其中试件SW-P1屈服荷载与极限荷载的增幅最大。 2)带型钢支撑试件的强屈比比对比试件都有所提升,可见支撑的存在一定程度上增大了剪力墙的塑性,提高了剪力墙的安全储备,其中试件SW-P1的强屈比提升比例最大,其次是试件SW-R,最后是试件SW-X1。 采用同级变形下的割线刚度来表示试件的刚度,割线刚度的计算方法如图12所示,即采用每级位移循环中的荷载最大值与其对应位移之比作为割线刚度[16],每一个循环的割线刚度取正向加载和负向加载的刚度平均值,最终的割线刚度取同一位移步长下两次加载的割线刚度平均值。采用上述计算方法得到的刚度退化曲线见图13。 图12 割线刚度计算方法Fig.12 Calculation method of secant 图13 刚度退化曲线Fig. 13 Degradation curves of secant 从图13中各试件的刚度退化曲线可知:所有试件的初始刚度基本相同,说明支撑的存在并没有改变试件的初始刚度,影响初始刚度的主要因素是混凝土的强度及构件的尺寸;从开始加载到屈服,所有试件的刚度均快速下降,其中带支撑试件的刚度下降速率要低于对比试件;从试件屈服到试验终止,所有试件刚度退化缓慢,其中带支撑试件的刚度均要明显大于对比试件的刚度;对比试验终止时试件的剩余刚度,SW-P1的剩余刚度最大,接下来依次为试件SW-R、SW-X1和SW-D。综上所述,加设型钢支撑能够有效地降低试件初期的刚度退化速率,也有利于试件后期的刚度稳定性,提高试件后期的抗震性能。 用延性系数作为衡量试件延性性能的主要参数。各试件开裂位移、屈服位移、极限位移及延性系数如表6所示。 对表6中各试件试验数据对比分析,能够得到:试件SW-X1、SW-P1和SW-R极限位移比对比试件SW-D分别提高了50.0%、85.7%和60.7%,其延性系数提高比例分别为14.5%、19.3%和5.0%,说明试件中支撑的存在能有效提高剪力墙的延性,且 SW-P1极限位移和延性系数提升幅度最大,其抗震延性性能表现最为优异。 表6试件的开裂位移、屈服位移、极限位移及延性系数 编号正向加载Uc/mmUy/mmUm/mm负向加载Uc/mmUy/mmUm/mm平均值Uc/mmUy/mmUm/mm延性系数Um/UySW-D6.007.5228.006.007.2528.006.007.3928.003.79SW-X16.009.8942.006.009.4542.006.009.6742.004.34SW-P110.0011.0052.0010.0012.052.0010.0011.5052.004.52SW-R10.0012.5046.008.0010.044.0010.0011.3045.003.98 注:Uc为试件的开裂位移;Uy为试件的屈服位移;Um为试件的极限位移,极限位移与屈服位移的比值Um/Uy为试件的延性系数。 1)由图14(a)可知,型钢混凝土剪力墙试件的混凝土应变范围较对比试件明显变小,说明型钢有效约束了试件混凝土的变形,增强了试件的抗变形能力。 2)由图14(a)可以看出,在3个型钢试件中,试件SW-P1的应变范围最小,且拉压应变分布基本对称,试件SW-R的应变范围较小,试件SW-X1的应变范围最大,这表明试件SW-P1的抗变形能力最好,SW-X1的抗变形能力最差。 3)由图14(b)可知,加载初期试件型钢应变较小,随着加载的继续,型钢应变不断增大,且逐渐表现为拉应变。 综上所述,与普通剪力墙相比,带型钢暗支撑的混凝土剪力墙抗震性能显著提高。屈服荷载和极限荷载都有很大提升,强屈比的提高增大了剪力墙的安全储备;刚度退化减缓,且后期刚度有所提升,剪力墙后期抗震性能稳定性好;极限位移与延性系数的提高可满足大震对墙体变形的要求;滞回曲线更加饱满,剪力墙耗能能力明显提高。在3种不同支撑形式中,又以加入竖向平行型钢对剪力墙抗震性能的提升效果最为显著。 图14 试件应变分析图Fig. 14 Strain analysis of 1)在低周反复荷载作用下,型钢支撑的存在可以延迟裂缝的出现,细化裂缝的宽度,有效增大剪力墙的塑性区高度。另外,试件SW-X1、SW-P1、SW-R和SW-D破坏形态基本一致,都属于弯剪型破坏。 2)型钢支撑明显的提高了剪力墙的开裂荷载、屈服荷载和极限荷载,也减缓了刚度的衰减速率,有利于结构的后期稳定,提高结构后期的抗震性能。 3)加入型钢支撑可以增大剪力墙的屈服位移、极限位移和延性系数,能够有效提升剪力墙延性性能,也提升了剪力墙在地震作用下的安全性能,加入型钢支撑的试件滞回曲线更为饱满,其耗能能力远优于普通剪力墙试件。 4)综合分析试验中各剪力墙的裂缝开展情况、承载力、应变、延性及耗能等抗震性能可以发现,型钢支撑的存在有效提高了剪力墙的抗震性能,其中在墙体中加入竖向平行型钢支撑对剪力墙抗震性能提升效果最优。在工程上,当剪力墙受到尺寸限制,配筋过多,或者普通配筋不能满足性能要求时,可在墙体中加入平行型钢支撑,不仅提高剪力墙各项力学性能,还能提高施工效率。 5)建议在混凝土剪力墙设计时,通过适当增加边缘约束构件配筋来提高剪力墙力学性能,在墙体内部加入竖向平行型钢支撑可以最有效地提高剪力墙的抗震性能。4.2 骨架曲线
4.3 承载力分析
Table5Crackingload,yieldloadandultimateloadofspecimens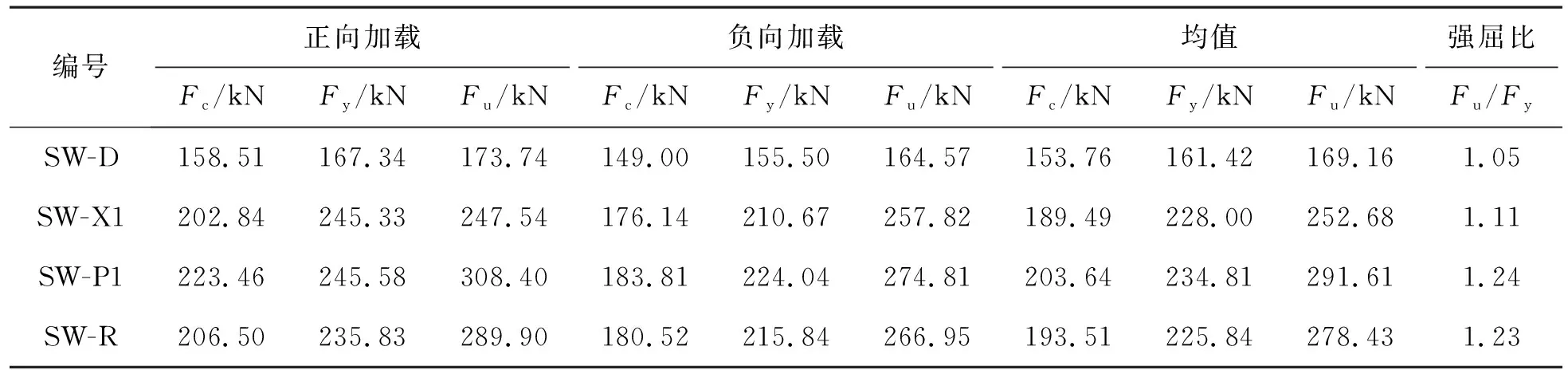
4.4 刚度退化分析
4.5 延性性能分析
Table6Crackingdisplacement,yielddisplacement,ultimatedisplacementandductilitycoefficientofspecimens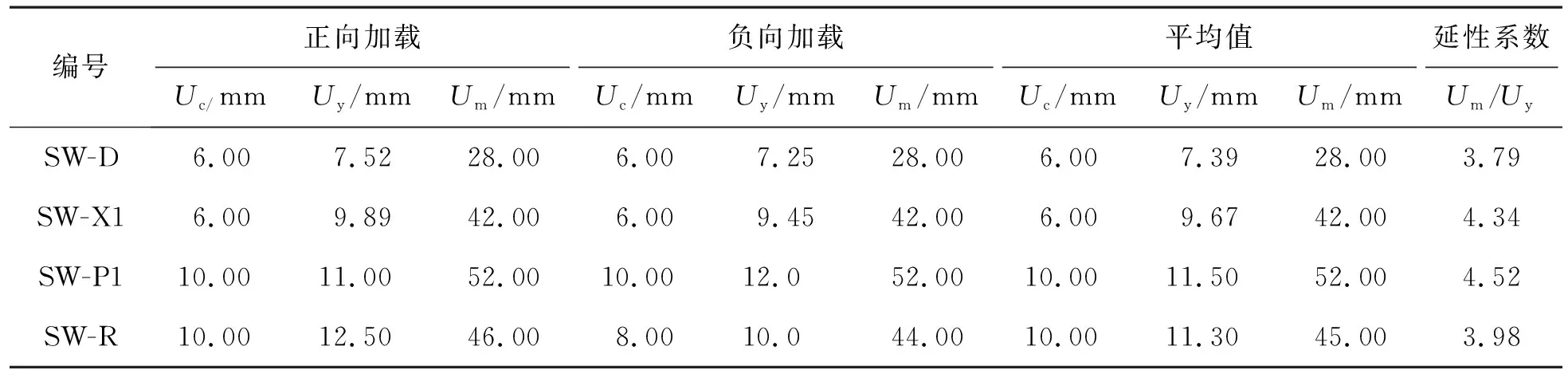
4.6 应变分析

5 结论
