压电微定位系统自适应鲁棒有限时间跟踪控制
2018-08-31康升征吴洪涛杨小龙程世利
康升征 吴洪涛 杨小龙 李 耀 程世利
(1.南京航空航天大学机电学院, 南京 210016; 2.盐城工学院汽车工程学院, 盐城 224000)
0 引言
随着生产制造及设备高精度需求的快速增长,微/纳技术得到迅猛发展。压电微定位系统(Piezoelectric micropositioning systems, PMS)作为这一领域的典型代表,因其结构紧凑、响应速度快、输出力大、分辨率高等优势,被广泛应用于超高精密定位行业中,如扫描探针显微镜、生物细胞操作、微机电系统组装等[1-2]。然而,由于PMS固有的迟滞、蠕变等非线性不确定因素的存在,若不加以控制,则会产生严重的开环定位误差[3-6]。
为了提高系统定位精度,无需建立迟滞模型的迟滞补偿控制方法引起广泛关注,如自抗扰控制[7]、滑模控制[8-14]、迭代控制[15]、模型参考自适应控制[16]等。上述方法一般将迟滞视为未建模不确定量或扰动项,然后构建一个鲁棒控制器进行补偿,从而避免迟滞辨识及求逆的复杂过程。在这些鲁棒控制方法中,滑模控制因其具有简单以及强大的处理不确定问题的能力而备受青睐[8-12]。文献[8-12]滑模控制策略中滑模面均是线性的,无法保证有限时间收敛。针对这一缺点并考虑到传统滑模控制依赖系统不确定量边界信息的不足,文献[13]设计了连续积分型三阶终端滑模控制律,并利用扰动估计(Perturbation estimation, PE)技术实现在线估计系统迟滞、外界扰动等不确定量。文献[14]同样基于PE技术设计了快速、无奇异终端滑模(Fast nonsingular terminal sliding mode, FNTSM)控制律。然而,在实际过程中,由于只有位置信息是可测的,而PE技术需要设计额外的状态观测器来实现全状态反馈,这样会增大控制器的复杂性。
鉴于FNTSM控制具有连续、无奇异、有限时间收敛特性,以及函数逼近(Function approximation, FA)技术无需全状态反馈且具有确定性及最小均方逼近[17]优势,本文将FA技术与FNTSM控制相结合,并引入具有结构简单、无需模型、可在线学习的模糊逻辑系统(Fuzzy logic system, FLS)作为补偿器。另外,利用Lyapunov函数设计自适应律,并证明闭环系统的稳定性。最后,通过仿真与实验验证该控制器的鲁棒性及有效性。
1 问题陈述
1.1 系统描述
一类含有非线性迟滞的二阶PMS的动力学模型可描述为[18]
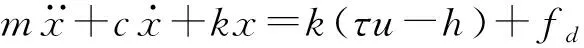
(1)
(2)
式中m——等效质量c——等效阻尼系数
k——等效刚度x——系统输出位移
u——输入电压τ——压电系数
h——迟滞变量
ζi——迟滞环形状的参数(i=1,2,3)
fd——未知但有界的外部扰动
此外,由于在实际的PMS中,模型参数可能会随操作环境的变化而变化,因此需考虑参数的不确定性。假设参数m、c、k、τ可表示成名义项及不确定项两部分,分别为m0+Δm、c0+Δc、k0+Δk、τ0+Δτ。因此,动力学模型(1)可重新描述为
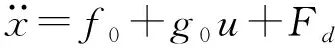
(3)
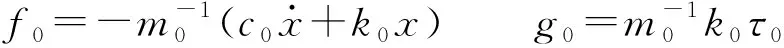
式中Fd——包括外界扰动、迟滞及未建模项在内总的系统不确定量
且满足如下假设:

根据方程(2)所描述的迟滞数学模型,若选取表1中所给定的系统参数值,以及输入电压信号
u(t)=5e-0.1t[sin(6πte-0.346t-1.5)+1]
则可得到如图1所示的迟滞效应曲线。从图1可以看出,PMS在开环情况下表现出强非线性,且随着控制输入电压频率的增大而越严重,影响了其精密定位性能。为了消除这一非线性迟滞,本文采用一种基于FA的自适应鲁棒有限时间控制策略来提高系统精密运动控制性能。

表1 仿真参数 Tab.1 Parameters of simulation

图1 PMS输入电压与输出位移的迟滞效应 Fig.1 Hysteresis effect between input voltage and output displacement of PMS
1.2 基于傅里叶级数的FA技术
对于任意分段连续的函数f(t),如满足Dirichlet条件,则可以用定义在区间[0,Tf]上的广义傅里叶级数展开形式表示
(4)
其中ωi=2iπ/Tf(i∈N)
式中ωi——正弦函数的频率
a0、ai、bi——傅里叶系数
定义
z(t)= [1cos(ω1t)sin(ω1t)…cos(ωNt)sin(ωNt)]T
(5)
w=[a0a1b1…aNbN]T
(6)
(7)
则式(4)可改写为
f(t)=wTz(t)+ε(t)
(8)
式中z(t)——正交基函数矢量
w——权系数矢量
ε(t)——估计误差
当N→∞时,误差ε(t)→0,因此只要N取足够大,f(t)可以近似表示为
f(t)≅wTz(t)
(9)
且估计误差满足
(10)
无论函数f(t)属于周期还是非周期函数,只要选择一个足够大的Tf,均能展开成式(4)的形式,并且当N取足够大时,也能够利用式(9)来估计该函数[17]。
采用式(9)来估计系统不确定量的优点在于它将未知的时变函数转换为时变的基函数矢量z(t)和常数矢量w。而根据式(5)、(6)中的定义,z(t)是已知的而w是未知的。因此,可以通过选择合适的Lyapunov函数获得自适应律来在线更新未知的常数矢量w。
由式(8)可知,估计误差ε(t)依赖于傅里叶级数的项数,且很难针对指定的精度要求进行选择。虽然可以通过增大傅里叶级数的项数来提高估计精度,但是伴随的计算量也会增加,因此实际估计过程中傅里叶级数项数是有限的,且误差总是存在的,为了减小估计的误差,需设计补偿器。为此,本文将引入FLS来作为补偿器,以提高系统的鲁棒性。
1.3 模糊逻辑系统
用来补偿估计误差的FLS的规则库可看成是从输入变量χ=[χ1χ2…χn]T∈Rn到输出变量ε∈R之间的映射,本文采用多输入单输出的IF-THEN规则,第j条模糊规则形式可表示为
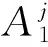
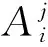
(11)
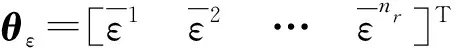
(12)
式中nr——模糊规则数


θε——可调节参数矢量
ψε——模糊基矢量
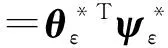
(13)
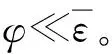
2 控制器设计
本文的控制目标为设计一种非线性鲁棒控制器,即使在PMS存在非线性迟滞及外界扰动等时变不确定情况下,也能使输出位移精确地跟踪期望位移轨迹。为此,定义位移跟踪误差
e=xr-x
(14)
式中xr——期望位移
假设2:期望位移xr为已知有界的时间函数,且二阶可微。
为了保证PMS快速精确地位置跟踪,定义连续无奇异终端滑模面[21]
(15)
式中:β>0,1<γ<2,符号sig(x)a=|x|asign(x)用来简化表达式。对于任意给定的初始条件,式(15)可在有限时间内收敛于平衡点,稳定时间为
(16)
对式(15)关于时间求导,可得
(17)
忽略外界扰动及系统不确定量,将式(3)代入式(17)可得等效控制输入为
(18)
同样,为了消除控制抖振并实现快速连续的控制,选择如下快速终端滑模型趋近律[21]
(19)
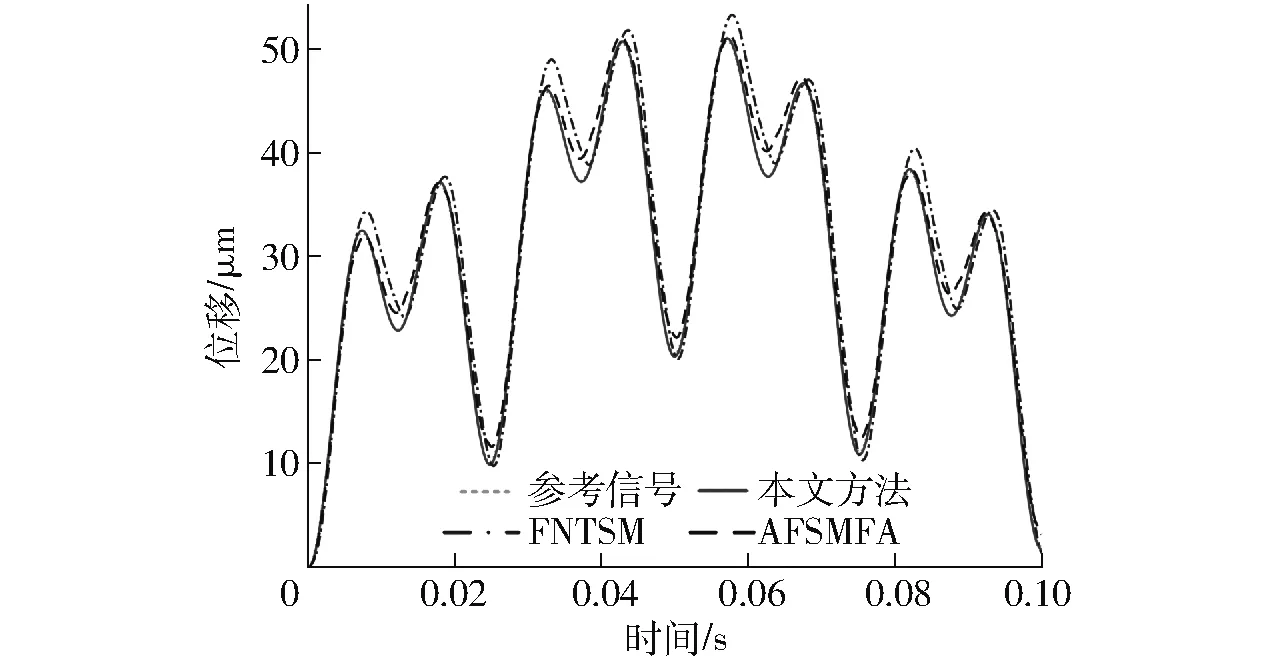
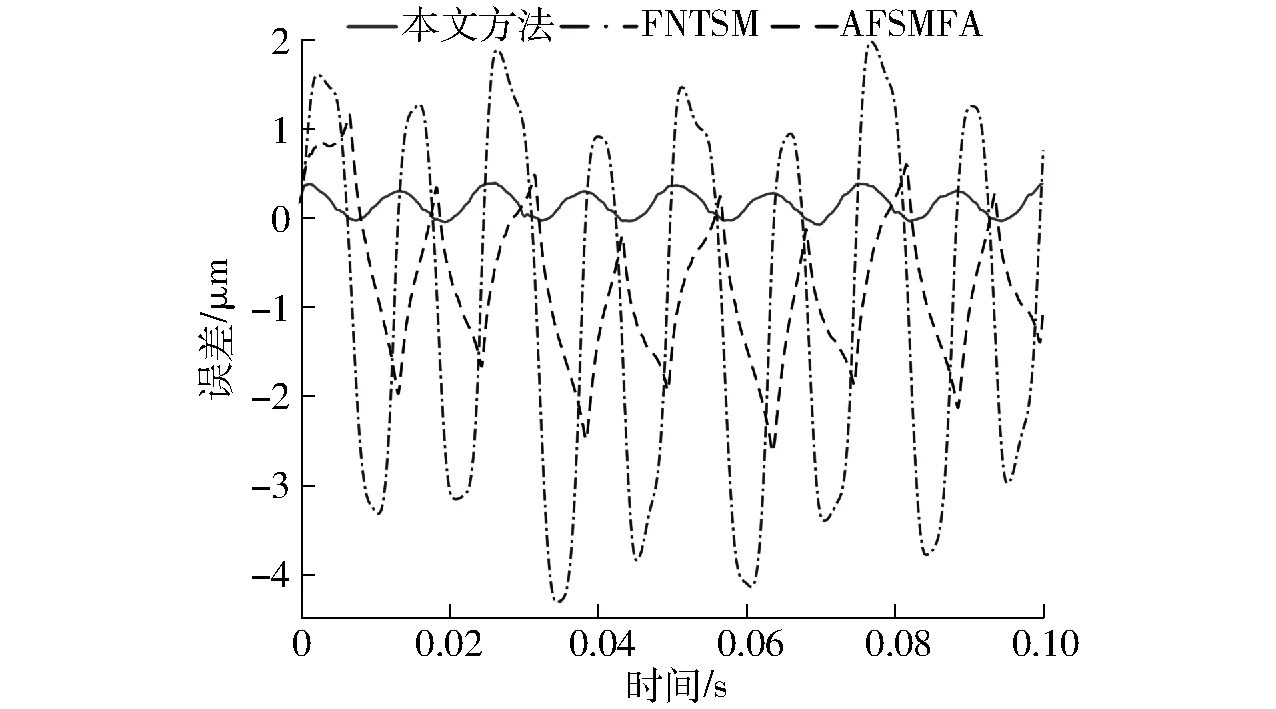
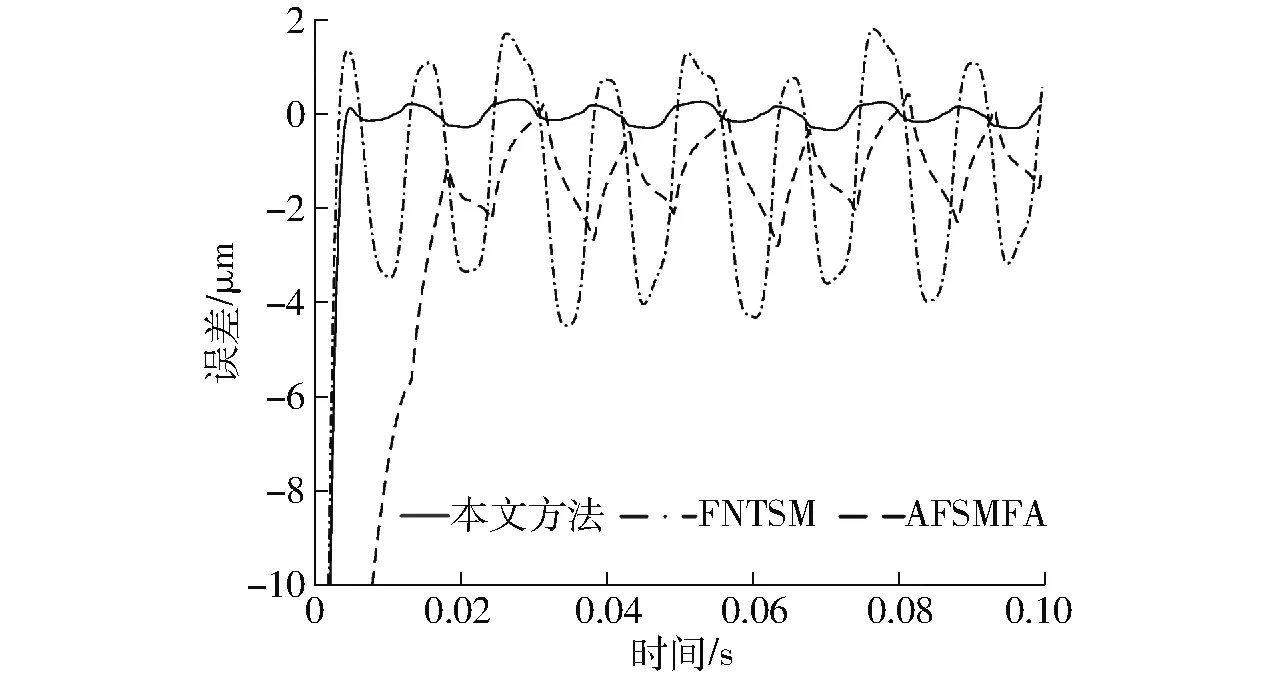
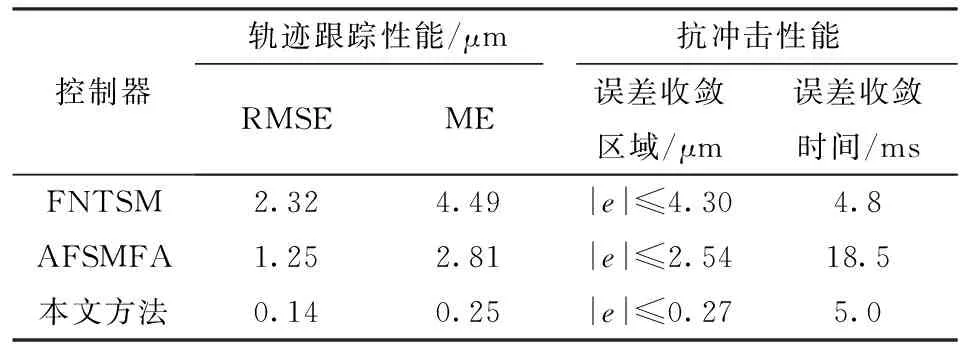
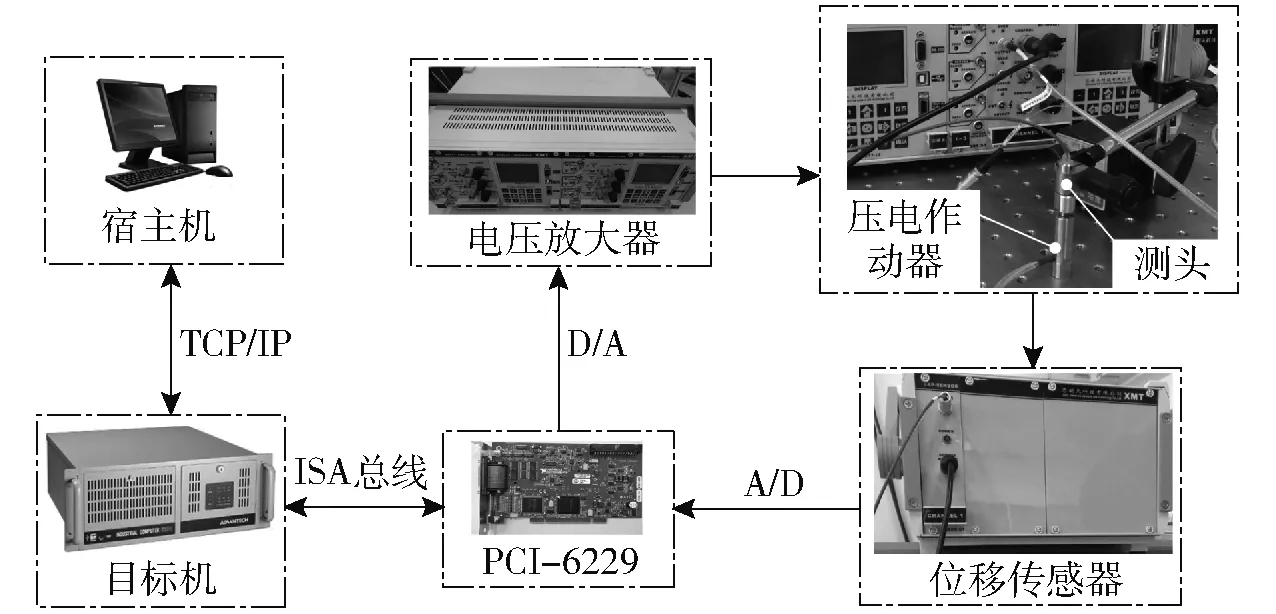
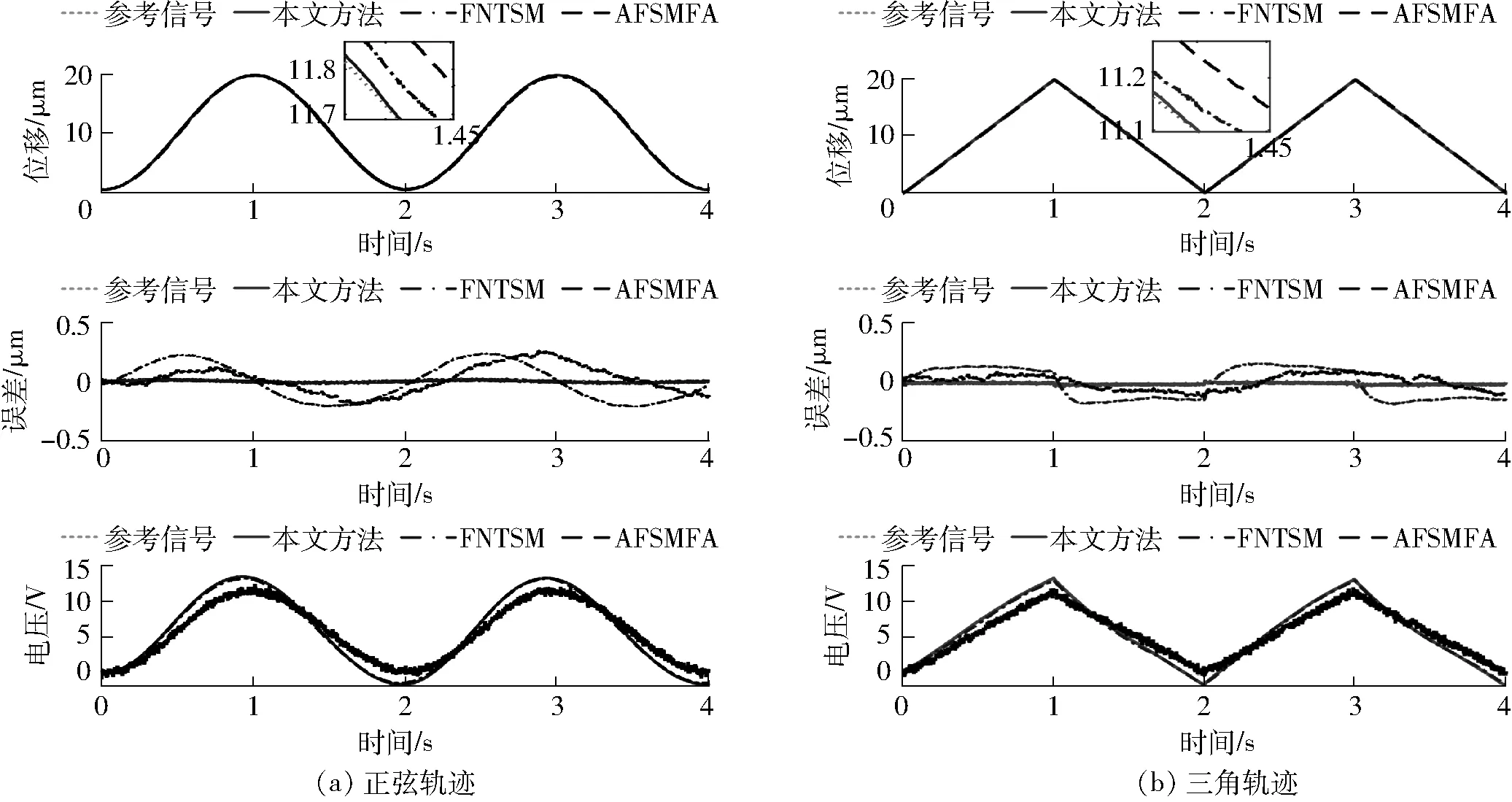
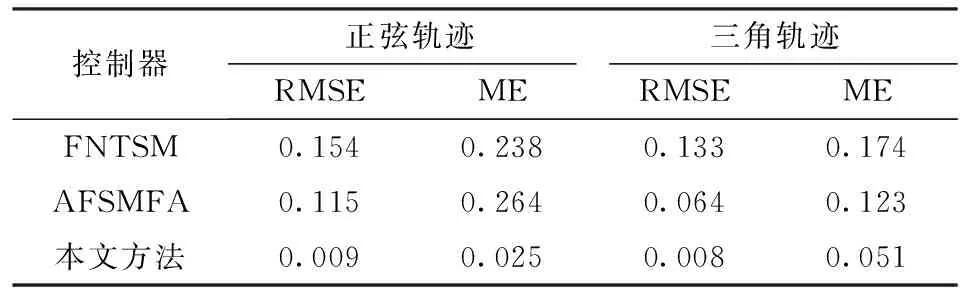
式中:k1、k2>0,0 (20) 根据滑模等效控制原理,传统的FNTSM控制律可设计为 u=ueq+ure (21) 鉴于传统的FNTSM依赖于Fd边界信息的不足,有必要对其进行估计。为此,本文将采用傅里叶级数进行动态逼近,并针对其逼近误差,再利用模糊逻辑系统实现在线补偿。根据上节的分析,可利用式(9)来逼近未知项,并针对估计的误差,由式(11)进行补偿,于是有 Fd=wTz (22) (23) 为了实现在线估计PMS的时变非线性函数Fd,避免反复试凑来选择估计函数,需要设计自适应律来调节式(23)中的傅里叶级数的系数以及FLS的调节参数矢量θε。因此,根据Lyapunov稳定原理设计了自适应律 (24) (25) 式中:η1、η2>0。结合式(23)、(21),于是可得到改进的FNTSM控制律 (26) 其中,ueq、d分别由式(18)、(23)给定。从式(26)可以看出,由于1<γ<2,0 图2 PMS控制器结构框图 Fig.2 Controller structure diagram of PMS 引理1:若存在Lyapunov函数V(x)满足一阶非线性微分不等式 (27) 式中:α、ρ>0且0<λ<1,那么对于任意给定的初始条件V0=V(x(0)),稳定时间为[19] (28) |e|≤2Δ=2min(Δ1,Δ2) (29) (30) 其中Δ1=|d-Fd|/k1Δ2=(|d-Fd|/k2)1/p 证明:定义Lyapunov函数 (31) 其关于时间的导数为 (32) 将式(3)代入式(17)中,并结合式(22)、(26)整理后得到 (33) 再将式(33)代入式(32)中整理后可得 (34) 为了推导出式(34)满足引理1中有限时间稳定条件,将其改写为 (35) (36) (37) (38) 综合式(37)、(38)的结果,滑模面可在有限时间收敛到区域 |s|≤Δ=min(Δ1,Δ2) (39) 为了证明跟踪误差及其速度收敛区间,将滑模面(15)改写成 (40) (41) (42) 至此,完成了定理1的证明。 根据定理1的结论可知,若Fd=d,则跟踪误差e及其速度理论上可在有限时间内收敛于零。即使实际中存在估计误差,通过将FA与FLS相结合的方式也能保证跟踪误差收敛到极小区域内。 由式(19)、(29)可知,选取的参数k1、k2越大,系统的收敛速率越快,且跟踪误差也越小。然而,增大k1、k2也会造成控制输入加大,导致实际中难以实现,另外还会产生抖振问题。因此在选择过程中需要权衡收敛速率与控制抖振。 本文所提的控制方法是基于文献[10]与文献[14]方法的改进。对比文献[10]提出的基于FA的自适应模糊滑模(Adaptive fuzzy sliding mode with FA, AFSMFA)控制,本文方法通过引入快速无奇异连续的终端滑模面,能够保证跟踪误差有限时间收敛于任意小区域内,且无抖振;而相比文献[14]基于PE技术的FNTSM控制,本文方法通过FA与FLS在线估计并补偿系统迟滞及外界扰动,不仅克服了FNTSM控制依赖系统不确定量边界信息的不足,且无需全状态反馈。 为了验证所设计控制器的有效性与优越性,对PMS精密定位控制进行了仿真研究,并分别对比了FNTSM及AFSMFA控制方法。其中FNTSM控制律与式(21)相同,AFSMFA的控制律为 (43) 式中λ1、λ2>0,其他参数均与本文所提控制器相同,以便于比较;sat(s/δ)为饱和函数,其边界层厚度为δ>0。 由于多频正弦信号在PMS中常用来作为跟踪均匀或非均匀曲面轮廓形状的参考信号[22],因此本文也选用该信号来验证所提控制器的跟踪性能。假设期望参考信号为 xr=40-10cos(2πt)-10cos(20πt)- 10cos(80πt)-10cos(160πt) 考虑到实际控制过程中,理想的跟踪性能一般都会受到高频测量噪声、外界扰动等影响,因此施加了时变干扰信号为fd=sin(200πt)+0.5rand,其中rand为区间[0,1]上的均匀分布随机数。各控制器参数选择如表2所示,其中相同的控制参数取值一致以便于比较。此外,为了衡量各控制器的性能,本文选用均方根误差(Root-mean-square error, RMSE)及最大误差(Maximum error, ME)作为评价指标,分别定义为 (44) ME=max(|xri-xi|) (45) 式中N——采样点数 xri、xi——第i个采样点的期望值与实际值 表2 控制器参数设计 Tab.2 Parameter design of controllers 根据上述仿真参数,可得到如图3~6所示仿真结果。由图3、4可看出,虽然3种控制器均能精确地跟踪参考信号,但是相比其他2种控制器,所提控制器的跟踪误差边界更小,其ME为0.25 μm,仅为参考幅值的0.5%。此外,由图5可知,在保证控制精度要求下,相比FNTSM控制,本文控制输入电压幅值更小,这是由于FNTSM的控制律依赖于系统不确定量边界信息,所选取的参数值存在过估计问题,导致输入电压增大;而对比AFSMFA控制,本文控制输入电压更光滑、无抖振,究其原因在于AFSMFA的控制律采用饱和函数作为趋近律,较小的边界层厚度虽然能提高控制精度,但相应也会造成抖振。图6为系统不确定量的估计误差,可以发现采用FA与FLS结合的方法相比于FA而言估计误差更小,这也正好验证了前文的理论分析结果。 图3 多频正弦轨迹跟踪结果 Fig.3 Multi-frequency sinusoidal tracking result 图4 轨迹跟踪误差曲线 Fig.4 Trajectory tracking error curves 图5 控制输入电压曲线 Fig.5 Control input voltage curves 图6 系统不确定量估计误差曲线 Fig.6 Estimation error curves of system uncertainties 为了进一步测试所提控制器的抗冲击性能,在相同期望参考信号下对PMS施加一个初始位移为50 μm的冲击扰动,仿真结果如图7所示。从图7可以看到,所提控制器稳定时间仅需要5 ms,跟踪误差即可收敛到0.27 μm内。相比之下,虽然FNTSM控制器稳定时间较所提控制器略短为4.8 ms,但跟踪误差收敛区间更大,达到4.3 μm;而AFSMFA控制器需要最长的时间18.5 ms才能稳定到2.54 μm,这是由于其采用线性滑模面,为渐进收敛,因而收敛速度更慢。虽然增大控制参数值可以减小误差边界并且提高收敛速度,但也会造成明显地抖振。 图7 冲击扰动下的轨迹跟踪误差曲线 Fig.7 Tracking error curves under impact disturbance 表3为上述2种测试条件下控制器的性能对比,可以看出所提控制器跟踪精度更高、抗干扰性能更强、响应速度更快。 表3 控制器性能对比 Tab.3 Performance comparison of controllers 为进一步说明所提控制器在实际PMS应用中的有效性,本文在基于Matlab/Simulink/xPC目标环境下,构建了以堆叠式压电作动器为实验对象的半物理实时仿真系统,实验设备如图8所示。同样分别与FNTSM及AFSMFA控制方法进行了对比。采样频率设置为10 kHz,各控制器参数按表2中仿真参数值进行实验。实验中,分别令3种控制器跟踪频率为0.5 Hz、幅值为10 μm的正弦及三角信号,跟踪控制结果如图9所示,各控制器跟踪性能如表4所示。 图8 实验装置 Fig.8 Experimental setup 由图9以及表4中可得,无论是对于正弦信号,还是不连续的三角信号,本文所提方法均能够实现最佳跟踪性能;相比之下,FNTSM控制方法跟踪误差最大,而AFSMFA控制的输入电压不光滑、抖振较为严重。上述结果与仿真结果是一致的,说明了本文方法是有效的。 图9 跟踪性能 Fig.9 Tracking performance μm 虽然相比FNTSM和AFSMFA控制方法,本文方法的优势是明显的,但需要注意的是,所设计控制器的跟踪性能会受到如下限制:① 傅里叶级数项数的选择需要权衡计算复杂度和估计精度,以便更好地进行实时控制。② 模糊规则及隶属度函数的设计依赖于设计者的经验知识。③ 控制参数k1、k2的选取需要综合考虑控制抖振和跟踪误差。 对于前两个限制,目前还没有明确方法,只能通过试错法找到最佳性能的参数;而对于第3个限制,虽然所提方法本质上是无抖振的,但对于高速及严重的时变不确定情况而言会有轻微的抖振现象,一种原因可能是采用常数控制增益难以实时平衡控制抖振和跟踪误差,因此可考虑利用自适应律来在线调节控制增益以获得更佳的跟踪性能。 针对PMS中普遍存在的外界扰动、迟滞等非线性、时变不确定问题,提出了一种由FNTSM控制器、函数估计器及模糊补偿器构成的鲁棒控制器。该控制器基于Lyapunov稳定原理,设计了傅里叶系数及模糊调节参数的自适应律,并实现了系统不确定量的在线估计和补偿。该控制器不仅保证了跟踪误差有限时间快速收敛,而且无需系统不确定边界信息。此外,该控制器的控制输入律本身是连续、非奇异的,因而抑制了控制抖振产生。在仿真及实验中,分别进行了轨迹跟踪及抗冲击性能测试,对比了AFSMFA和FNTSM方法,结果表明,本文方法可实现最佳跟踪性能。

3 稳定性分析
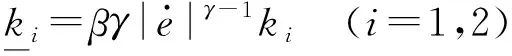
4 仿真
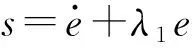

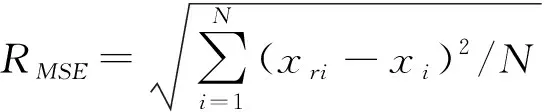



5 实验验证
6 结束语
