电力系统潮流不收敛机理分析

，，，

(1.国网吉林省电力有限公司松原供电公司，吉林 松原 138000 ；2.松原电力勘测设计有限公司，吉林 松原 138000)

1 引言

潮流计算是电力系统分析中最基本的计算，是电力系统稳态、动态分析的基础。

目前，潮流计算中应用最广泛的方法是牛顿拉夫逊法，随着电力系统规模不断扩大，系统节点数增加，雅可比矩阵阶数增加，可逆性降低，容易出现迭代不收敛的情况。此外，电力系统工况实时变化，一旦不能满足系统约束方程，也可能会造成潮流不收敛的情况。

针对电力系统潮流不收敛问题，调度人员通常反复调整潮流数据，通过经验对系统潮流分布做出判断[1]。但在大系统中，没有目标地反复调整数据费时费力，因此，潮流计算不收敛机理分析是一项亟需研究的课题。

目前针对电力系统潮流不收敛问题的研究主要针对于病态潮流的计算方法上。文献[2]针对含有小阻抗支路接地系统，提出牛顿拉夫逊法通过提高电压启动值可以缓解不收敛问题。文献[3]将牛顿法与内点罚函数法结合，文献[4]将牛顿拉夫逊法的极坐标方程进行修正，提高潮流收敛性。

基于以上背景，本文分析电力系统潮流计算不收敛的数学机理和物理机理，最后通过西北电网对本文结论进行验证。本文的研究对电力系统潮流计算不收敛数据的调整具有一定的指导意义，具有较大的工程应用价值。

2 潮流不收敛的机理分析

2.1 数学机理

牛顿拉夫逊法是将非线性方程f(x)进行泰勒展开约去高次项得到[5]：

(1)

通过Δx(0)对x(0)进行修正，得到x(1)，再重复迭代，直到第n次的Δx(n)满足精度为止。

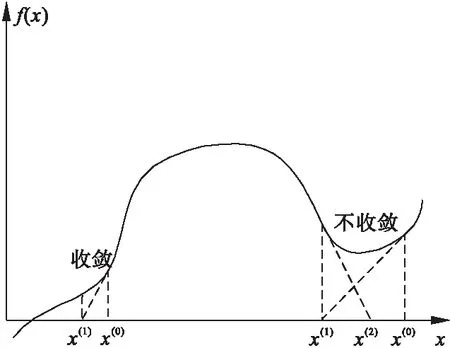
图1 牛顿拉夫逊求解过程

如图1所示，当初值x(0)接近精确解时，方程收敛，当x(0)与精确解较远时，方程不收敛。

2.2 物理机理

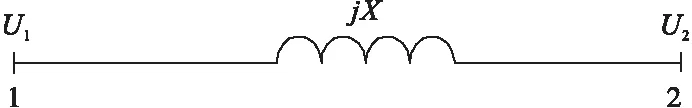
图2 两节点系统

如图2所示，设功率从节点1流向节点2，1节点电压为U1，2节点电压为U2，不计电阻，两节点间电抗为X，线路末端的有功、无功功率为：

(2)

(3)

其中，I2为注入节点2的电流。U1与U2间的幅值差可以表示为：

(4)

由公式(4)可知，当无功功率Q2、线路电抗X较大时，U1与U2间电压降落明显，若U1一定，则U2会较低，但根据公式(3)可知，U2过低会使线路输送的无功功率受限制，使得方程ΔQ=0在迭代过程中会出现不收敛。同理，当U2初值较低也会造成方程ΔQ=0迭代过程中不收敛。

此外，根据公式(2)可知，当U2过低，也可能会造成ΔP=0在迭代求解过程中不收敛。

根据以上分析可知，当线路电抗过大、线路功率过大、节点电压初值过低均可能造成潮流计算不收敛。

3 算例分析

本文采用西北电网进行算例分析，验证本文结论，仿真工具采用Matlab工具箱PSAT。西北电网地理接线图如图3所示。图中的直流外送均假设为无穷大系统，并将所有无穷大系统等值为一个无穷大系统。采用牛顿拉夫逊法计算该系统潮流，迭代4次后结束。

图3 西北电网地理接线图

将西宁800kV母线电压初值从1.0p.u.改为0.1p.u.，计算该系统潮流，迭代7次后ΔP开始发散，迭代第18次时计算停止，系统潮流不收敛。系统中拉西瓦装机3500MW，出力为2800MW，当西宁母线电压过低，大大减少了拉西瓦水电向西宁输送的功率，而拉西瓦向官亭的功率到达输送极限，导致拉西瓦水电有功不能全部送出，最终潮流不收敛。

将拉西瓦水电装机改为35000MW，出力改为28000MW，系统潮流不收敛。这是由于有功出力过剩，外送能力有限，导致功率方程无解。

将拉西瓦水电升压变压器等值电抗由0.0066p.u.改为0.66p.u.后，计算系统潮流，迭代6次结束。相比于原系统，电抗增加后，收敛速度较慢。继续增加拉西瓦变压器电抗，改为6.6p.u.，潮流不收敛。

由以上仿真分析可知，当母线电压初值过低、功率过剩、电抗过大均会导致系统潮流不收敛。

4 结论

本文分析了电力系统潮流不收敛的数学机理和物理机理，通过分析可以得出结论：当母线电压初值过低、发电机功率过大、电抗过大均可以导致系统潮流不收敛。最后，通过西北电网验证本文结论有效性。本文的工作为解决电力系统潮流不收敛问题提供理论指导，具有一定工程应用价值。