格点多边形遇上毕克公式

李沁霖

“丁零零……”下课了！悠悠急匆匆地跑来，说：“小霖啊，现在的题目真是麻烦。你看这个图形（图1），已知每一个小正方形的面积均为1平方厘米，求阴影部分四角形的面积。这怎么求呀？”

我接过题目仔细一瞧，呵呵笑道：“这个题目其实不难。把图形分割成我们熟悉的正方形和三角形（图2），那么四周每个小三角形的面积是2×2÷2=2（平方厘米），中间正方形的面积是2×2=4（平方厘米），所以四角形的面积为2×4+4=12（平方厘米）。”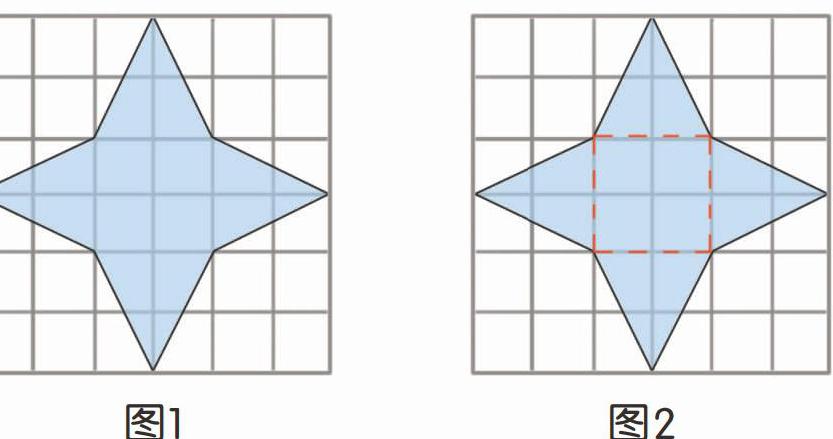

悠悠点点头，说：“是哦，这样一分割就简单了！”

“其实啊，这个题目还有更简单的解决方法。那就是根据它内部格点数和周界上的格点数，得出四角形的面积是9+8÷2-1=12（平方厘米）。看，是不是简单了许多？”

她不可置信地说：“啊，这怎么可能？这是为什么呢？”

我神秘地一笑，说：“这类题目呢，就是格点问题。一个多边形的顶点如果全是格点，这个多边形就叫格点多边形。这种格点多边形的面积计算起来其实不难，一般有三种方法。你知道是哪三种吗？”

一旁的晴晴笑着凑过来，说：“我知道！规则的格点多边形，可以运用多边形的面积公式求出面积；而一些简单而又特殊的格点多边形，可以通过数格子求出面积。但是数格子的方法比较原始，很少用。”

“那还有一种方法是什么呢？”悠悠忙追问道。

晴晴不慌不忙地回答：“较复杂的不规则格点多边形，一般用毕克公式计算。对任意格点多边形，只要数出多边形周界上格点的个数及图内格点的个数，就可以用毕克公式算出面积：格点多边形面积S=图内格点个数N+周界格点数L÷2-1，即S=N+L/2-1。

“我好像懂了。”悠悠兴奋地点点头。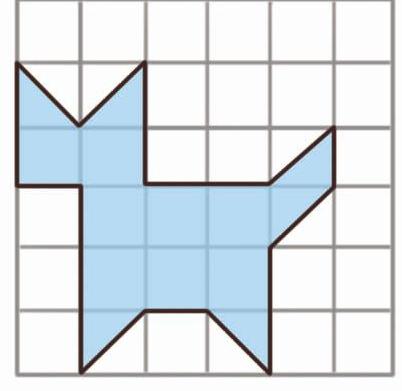

我随即说道：“那我们来做道题热热身吧！”说罢，我便在纸上画了一个格子图。

悠悠想了想，立即报出了答案：“内部格点数2个，周界上格点数20个，面积为2+20÷2-1=11（平方厘米）。”

“不错，就是这样。”我点了点头。

悠悠感叹道：“数学真是奇妙呀！之前觉得很难的图形題，现在因为这些不可思议的方法又觉得很有意思。”

数学真是无处不在，同一道题目可以有不同的解法，我们要善于思考，勤于动脑，发现每一个小细节。

冯煜琪7月7日 10：10：22

原本看起来很难的题目，经过小霖这么一讲，立马就变简单了！

朱菲扬 7月7日 11：35：12

这么难的题目都能轻松解答，真厉害！

黄煦婷7月7日 11：40：25

小霖用简单易懂的方法告诉我们如何求解格点多边形面积，让我受益匪浅。

徐铭蔚7月7日 12：22：43

数学中藏着奥秘，小霖巧妙的解题方法让我豁然开朗，激发了我探索数学奥秘的兴趣。