芦果漫游数题国之四角相消长

卢声怡

上一期，芦果从落单的备用轮子滚动中，成功解释了亚里士多德的“轮子悖论”，这算是意外收获吧！这一期，芦果继续漫游数题国。听，是谁在吵架？哦，原来是四个角啊！它们在吵什么呢？想知道？那就往下看吧！

“这辆车居然被自己的轮子追尾了。”芦果和青鸟大笑不已。还没等青鸟笑完，芦果突然想起一个关键处，她认真地向青鸟指出：“我跟你说不想看纯粹图形的数题故事，想看有人物的。你倒好，找的人物是坐在车里的司机，而且跟这数题故事也没啥关系，我们归根到底，还不照样看的是图形——轮子。”

“想看人物呀？简单，我们找有人声的地方去就是了。”青鸟背起芦果，重新飞到天上。他们往前飞了一阵，果然听到下方传来吵吵闹闹的声音。

芦果大喜，拍拍青鸟的脑袋说：“下面肯定人很多，我们降落吧！”

青鸟歪歪脑袋：“第一，你能不能尊重一下老师，不要拍我的脑袋。第二，我觉得下面人不多，好像只有几个。”

芦果不好意思地收回手来，问：“你怎么知道只有几个？明明这么吵。”

“我走南闯北见多了，都说三个女人一台戏，听这声音，我敢肯定那是几个女……”青鸟一降落到地上，就把最后一个字给吞了回去，因为前方不远处，围成一圈争执不下的，是几何图形中的四个角。

在数题国中，与数学有关的事物都有可能变成人物，有眼耳口手，能坐卧立走，会说话，能指手画脚……这些芦果都已经见怪不怪了。不过她发现这四个角与之前见过的角不一样，它们的大小不确定，组成角的两条边随着它们的说话声忽闪忽闪，开开合合。

看出了芦果的疑惑，青鸟解释说：“如果一道数学题中，明确说某个角是多少度，那就叫‘常量，而这几个角都不是固定不变的，叫‘变量。”

“嗯？”芦果有点发懵，“什么样的数学题会有这样的角呢？”

“你看！”青鸟右翅膀往前一指，在四个吵闹的角的后方空中，赫然排列着一些文字。

芦果认真读完题，明白了：“就是说这四个角的度数不确定，否则我们只要算一下就知道答案了。”

青鸟笑了：“当然，要不怎么算难题？我曾经见过你们一次数学竞赛中就有这道题。”

芦果吓了一跳：“数学竞赛题？我连老师课内布置的作业题都有不会的，更不要说数学竞赛题了，难怪这么难。”

青鸟却说：“要不是有这些难题，也不会有数题国了。正是人类对数学的思考，让一道道的数学难题组成了这个充满挑战的国度。”

“难怪数学老师说要‘绞尽脑汁，看来我们的‘脑汁就是数题国的能量来源呀！”芦果大叫起来。

青鸟把手放在嘴前，做了个噤声的动作，小声说：“嘘，你先不要说话，我们偷偷观察一下它们的情况。”

芦果笑了起来：“你不是说，数题国的人物听不到我们说话吗？”

“但是我听得到你说话，你太吵啦！”青鸟的话让芦果脸红得不敢说话了。

青鸟拉着芦果的手，往前走了几步，细心观察起来。他们发现，四个角的大小是有联系的，特别是当两个角安静的时候，如果一个角变大，则另一个角肯定变小。

芦果记起来了：“数学题中说的是四边形，这四个角肯定就是那四边形的四个内角，而四边形的内角和是360度，只要其中有角变大，肯定就有其他的一个或几个角变小。”

青鸟赞赏地看看她：“你这徒弟的数学也不是太差嘛，都知道‘四边形的内角和是360度了。”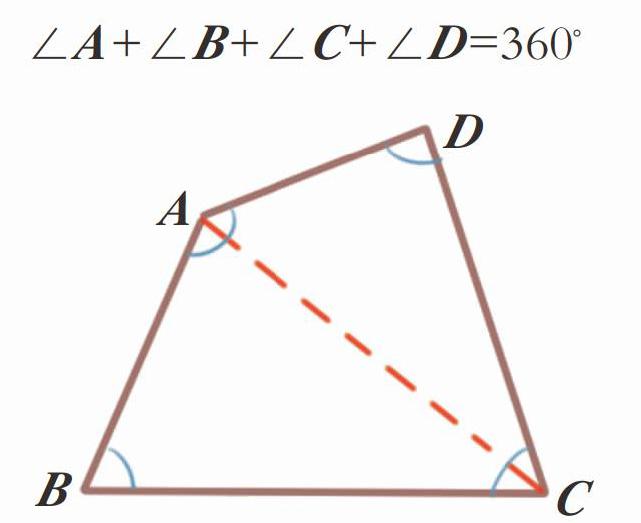

“简单啊，课本上教过‘三角形的内角和是180度，而所有四边形不是都可以切成两个三角形吗？原来的四个角正好就变成了两个三角形的六个角，180×2就是360了。”

“对，你瞧角A在变大，角D没变，明显角B和角C在同时变小，而且少的度数就是角A多的度数。”

“总之，这四个角的和是360度，这可是数学题中没明说的。”

“棒！”青鸟一拍翅膀，发出轻柔的响声。

芦果和青鸟为他们点破了一个重要条件而欢呼，而那四个角的讨论还在继续。

角A说：“咱们四个角是互相影响的，此消彼长四兄弟，谁要想大于180度是不可能的。”

角B提醒道：“不是谁想大于180度，现在我们要表演的是‘取2个角求和，然后问‘大于180度的和最多有多少个。”

角C说：“那我们就别计较每个角的大小了，应该先来想想这个‘和。现在的问题是，我们四个角能组成几个‘两角和呢？”

“简单啊，牵牵手，或者列举一下就知道了。”

在角D的指挥下，角A和角B、角A和角C、角A和角D、角B和角C、角B和角D、角C和角D，一共握了六次手，所以有6個和。

芦果小声跟青鸟说：“这是我在低年级数学课本上就学过的，如果按顺序不重复地想，可以列式3+2+1=6。”

“你这是它们刚刚说的顺序法。”

“但我觉得还可以列式4×3÷2=6，也很快。”

“这个算式的意思是每个角都跟另三个角分别相加，但这样得到的和会重复，所以最后把数量再缩小到一半。”

“总之这个不算难点，但我不知道怎么才能明白在这6个和里面，最多有多少个是大于180度的，如果它们能表演给我们看就好了。”

芦果的如果二字一出口，就像她漫游数题国在沿路上多次看到的那样，面前的四个角突然就变起来了。

角A对角B说：“先下手为强，我们先把我们的和大到180度以上再说。”

说完，它们俩很快拼成了一个比平角还大的角，兴奋地叫着：“哈哈，我们是‘优角啦。”

角C和角D此时也合为一体，哎哟哎哟地叫着，拼成了一个比180度小的角。

角AB（此时它们合体成一个角了）得意地说：“哈哈，因为总和只能是360度，我们俩如果比180度大，你们俩就只能比180度小。”

芦果若有所思。

青鳥冷笑了一下：“难道就不能是角C和角D合并比180度大吗？” 芦果说：“那样的话，角AB就比180度小了。哈哈，我发现‘AB和‘CD两个和是成对的，它们总是一个大于180度，另一个小于180度，不可能全大于180度，也不可能全小于180度，是‘此消彼长呀！”

青鸟启发她：“那如果是角B和角C的和大于180度呢？”

芦果不假思索地说：“此消彼长，那么角A和角D的和就小于180度。”

“你怎么知道？”

“喏，你看。”芦果一指前面，青鸟笑了。眼前的情景已经变成角A和角D合伙在变大，与此同时角B和角C的和在变小。

“这样就简单了。”芦果向前一伸手，想把边上的一根灌木树枝折下来写字。可是她觉得手收回来时，手心里的感觉很奇怪。定睛一看，握在手里的居然是刚才的ABCD四个角，只是此时它们的边变短了许多，但角度的大小不因边的长短变化而变化，所以四个角的大小和原来是一样的。

四个角就像被巨人捏在手中的四只小鸡一样，着急得叽叽乱叫，却说不出完整的话来。

芦果就用这四个角在面前摆起来。当她摆好再收起来后，原处仍会留下这些角名称的痕迹，所以可以反复摆弄。

芦果指指她摆好的那些“两角和”的名称，不说话。

青鸟哈哈笑起来，连连点头：“你这么一排列一分组，果然就明白了。”

原来，芦果把刚才的6个“两角和”列成了两列，左边是角A角B、角A角C、角A角D，右边对应的是角C角D、角B角D、角B角C。

青鸟赞许地对芦果说：“很明显，左边这列的三个大于180度的话，右边那列的三个就小于180度了。反过来也一样，总之最多是3个和大于180度。”

被青鸟说出了问题的正确答案，面前的那道数学题连同这些角人物齐发出“砰”的一声，爆成烟雾，转眼散尽了。

芦果望着已经消失的数学题，叹息：“我原来一直觉得如果是竞赛中的数学题，那肯定是我想不出来的难题。通过这次的问题，我觉得理清思路后就豁然开朗了呢！”

“那，我们回忆一下。首先你通过观察发现了‘四个角的总和为360度这个隐藏条件，然后你按题目要求，列举出了‘6个两角和，最后你观察这些两角和之间的变化规律，发现它们是成对的，此消彼长，分成两列，答案就跃然眼前了。” 青鸟总结道。

“太有意思了，在这数题国中遇到的每道题都让我大有收获呢！”

芦果的话让青鸟不禁开心起来。

从四边形4个内角中取2个求和，共有6个度数，则大于180度的和最多有多少个？

青鸟请你漫游数题国

相信你已经看懂芦果和青鸟的思路了。不过故事中的问题还能这样想：因为四个角不可能全是锐角（想想为什么），所以至少有一个是直角或钝角。从这个前提出发，画一下图，你也能找到正确答案，试试吧！（答案见下期）

芦果和你对答案

上期答案：两个同心的正方形，当大正方形翻动4次（正好前进了正方形轮子的周长）时，可以发现小正方形被带着跳过了3段距离，这恰恰说明轮子上的圆不止有滚动，还有平移运动。