基于反射波时距曲线计算地层速度

高 瑀

（长安大学 地测学院， 陕西 西安 710021）

1 模型建立与观测系统设计

1.1 两层倾斜层状模型

建立两层倾斜层状模型，模型尺寸为1000m*500m，第一层速度，第二层速度v2=2250m/，第二层为半无限体，界面倾角为φ=8.7°。

设置1个激发点位于（300，0）位置，激发点到界面的垂直距离h1=205.1m，接收排列长度为600m，接收点距为5m，接收道数为121个，接收排列起始点位于（0，0）位置。设置记录长度为1000ms，采样率为1ms，地震子波采用主频为50Hz的雷克子波。

1.2 三层水平层状模型

建立三层水平层状模型，模型尺寸为1000m*500m，第一层速度v1=1000m/，厚度h1=100m ，第二层速度h1=2000m/，厚度h2=200m ，第三层为半无限体，速度为 v1=1000m/。

设置1个激发点位于（500，0）位置，接收排列长度为800m，道间距为5m，接收道数为121个，接收排列起始点位于（200，0）位置。设置记录长度为1000ms，采样率为1ms，地震子波采用主频为50Hz的雷克子波。

2 模型计算

2.1 两层倾斜层状模型

二层倾斜层状模型中，下倾激发上倾接收折射波时距曲线为

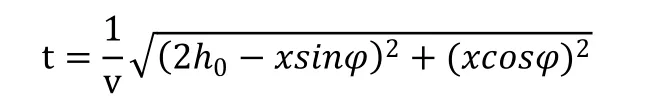
两边同时平方，移项并化简得

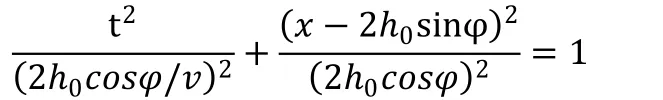
时距曲线是双曲线，双曲线极小值位于处。

上倾激发下倾接收折射波时距曲线为

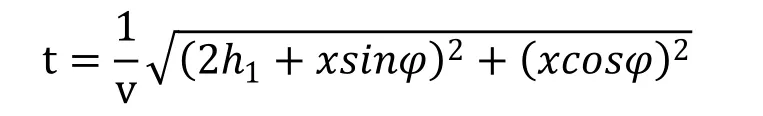
两边同时平方，移项并化简得

时距曲线是双曲线，双曲线极小值位于处。

在相遇观测系统中，由互换定理可知

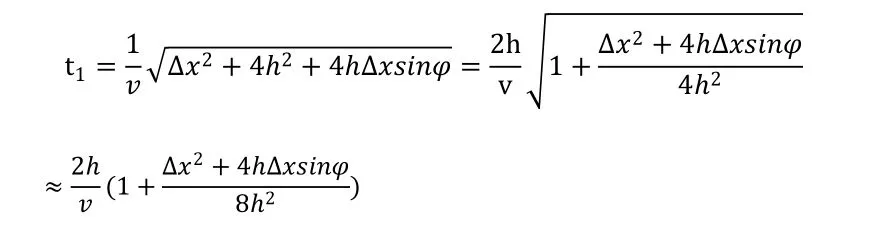
同理，

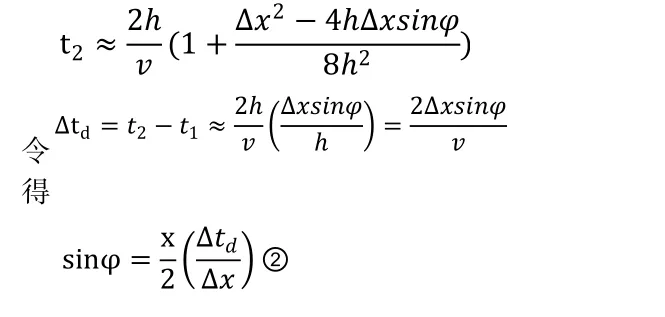
其中φ为地层倾角，h0为下倾激发点到界面的垂直距离，h1为上倾激发点到界面的垂直距离。

从上述公式①可知，反射波双曲线的极小点向界面上倾方向移动，移动距离等于 sinφ=2×205.1×sin8.7°=62m ，因此极小点位置为362m。

由于双曲线的极小点位置发生移动，因此制作共激发点道集的叠加速度谱时，需要修改激发点位置至362m。设置速度范围为500 ～ 3000m/s，速度增量为50m/s，拾取叠加速度谱中聚焦能量团，速度值见表1。

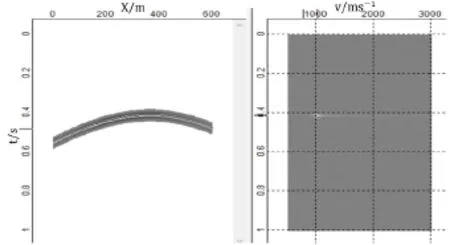
图1 叠加速度谱（两层倾斜层状模型）

表1 速度拾取（两层倾斜层状模型）

2.2 三层水平层状模型

对于第一个分界面，其反射波的时距曲线方程为

对于第二个分界面，其反射波的时距曲线方程为

其中，h1为第一层地层的厚度，h2为第二层地层的厚度。

制作共激发点道集的叠加速度谱，设置速度范围为500 ～ 4000m/s，速度增量为100m/s，拾取叠加速度谱中聚焦能量团速度值见表2。

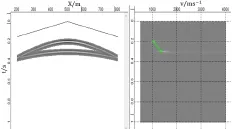
图2 叠加速度谱（三层水平层状模型）

表2 速度拾取（三层水平层状模型）

3 误差分析

3.1 二层倾斜层状模型

对于共激发点道集，二层倾斜层状模型，叠加速度等于层速度。由表1可知，第一层层速度与真实速度1000m/s相比，存在0.87%的误差，

误差量小。联合叠加速度谱中获得的自激自收时间t0=0.408s ，可以计算第一个反射界面深度，与真实反射界面深度 205.1m相比，存在0.34%的误差，误差量小。

为了求取反射界面倾角，根据公式②，取 ∆x=150m，读取t1=0.464s、t2=0.418s 。

表3 二层倾斜层状模型结果分析表

3.2 三层水平层状模型

三层水平层状模型，叠加速度等于均方根速度。由表 2可知，第一个反射界面均方根速度，即第一层层速度 vint,1=998.2m/s ，存在-0.18%的误差，误差量小；第二个反射界面均方根速度根据迪克斯公式计算第二层层速度

真实第二层速度为2000m/s，存在-4.2%的误差，误差量较大，可能在速度拾取中存在误差。联合叠加速度谱中获得的自激自收时间 t0,1=0.196，可以计算第一个反射界面深度，与真实反射界面深度100m相比，存在-2.2%的误差，误差量小。

同理，联合叠加速度谱中获得的自激自收时间 t0,2=0.297，可以计算第二个反射界面深度，与真实反射界面深度200m相比，存在2.5%的误差，误差量小。

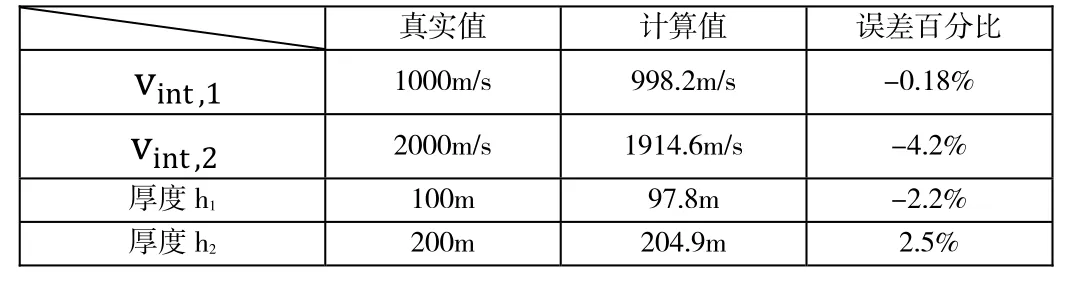
表4 三层水平层状模型结果分析表

4 结论

速度分析及求取层速度是反射波勘探地震中的主要问题，对于浅地表起伏不大的地区，可在建立了合适的观测系统后，采用双曲时距曲线方程求取层速度和厚度。若地层分层较少时，该方法所求的地层速度误差较小，且该方法求多层地型厚度时，不受上一层厚度值的影响，相比较折射波时距方程求取地层厚度方法更优。误差主要来源与于叠加速度谱中速度的拾取，速度的准确度影响了层速度及厚度的准确度。