基于贝叶斯方法的西江流域大雨集合概率预报产品订正试验

曾鹏，钟利华，李勇

（广西气象服务中心，南宁530022）

引言

西江流域降水丰沛，河谷纵横，水力资源丰富，是我国重要的水电开发基地。水能资源的利用与气象条件密切相关，广西电网直调水电厂分布在珠江上游的西江干流上，其所处的地区地形较复杂，强降雨的突发性强，时空分布不均匀，对广西电网各水电站的蓄水发电、电力调度和防洪抗洪等生产活动具有重要影响，针对该区域的降雨预报预警已开展了许多研究工作[1-5]，取得了一定成果。

大气降水在时空分布上的变化很大，因此对定量降水预报的可靠性提出了很大的挑战，由于模式的初值误差、模式误差和大气系统的混沌性，使得数值预报存在不确定性[6-7]，为了克服单一数值预报模式预报降水的不确定性,近些年来,在天气预报领域开展了集合预报技术研究[8]，发展了多模式至多分析集合及其概率预报技术，并且已经应用到多种尺度的数值预报中，逐渐促进了由单一化的确定性预报向概率预报的延伸和发展[9-10],使降水的预报技巧有了一定提高。集合预报系统会产生大量的预报结果，现已有很多集合预报解释应用的方法[11]，如集合平均图、集合预报离散度、面条图、概率烟羽图、各种聚类方法等。相较于确定性预报，从集合预报的结果中更加容易提取出极端降水的概率，把该概率作为先验概率，将贝叶斯理论应用于集合预报产品的解释中，是近年来集合预报应用的一个新趋势，其优势已经得到了国内外众多水文气象学家的肯定，并促使国际上初步形成了一些新的大型水文气象集合概率预报计划[12-13]。

由于针对西江流域开展集合预报技术与产品应用的研究较少，本文在已有研究的基础上，利用贝叶斯方法，探索从集合预报提供的降雨概率预报产品中，提取更好体现强降雨概率预报价值的信息，进而建立西江流域降雨概率预报方法模型，为广西电网直调水电站开展强降雨预报预警服务提供科学合理的决策依据。

1 资料与方法

1.1 预报与实况资料

本文所用的预报资料为ECMWF（European Centre for Medium-Range Weather Forecasting）集合预报的降水资料，资料的起报时间为12 时（世界时），集合预报成员数为51个，时间长度为2016年4～9 月，预报时效为24～72h，水平分辨率为0.5°×0.5°。实况观测降水资料采用基于国家气象信息中心基础资料专项最新整编的中国地面高密度台站的降水资料，利用薄盘样条法（TPS，Thin Plate Spline）进行空间插值，形成中国地面水平分辨率0.5°×0.5°的日值降水格点数据，资料长度为1981～2016年4～9月。本工作研究的是所选区域各个格点达到大雨及以上（≥25mm）的降雨，由于预报与实况资料均为格点数据集且格点位置一致，可以直接进行对比分析。

1.2 研究区域

根据广西电力部门的服务需求，研究区域为西江流域中上游和广西沿海流域，包括广西区域、贵州南部和云南东部地区，位于北纬21.40°～26.95°，东经102.25°～112.06°。参照文献[3]的小流域分区，将西江流域分为24个流域区间，本文将对24个流域区间内降水格点场进行集合概率预报产品的应用分析。通过GIS技术对降水格点场进行筛选，形成研究区域内的格点数据集（图1）。

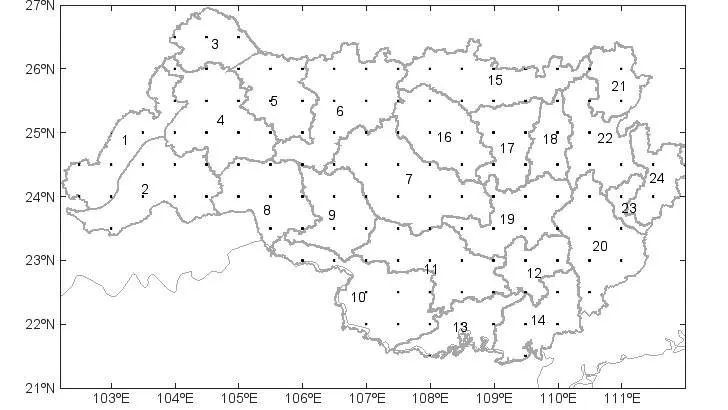
图1 西江流域分区及研究格点位置示意图

1.3 贝叶斯方法简述

贝叶斯方法是多因子条件概率的一种综合方法，其原理是将预报因子历史样本获得的先验信息与预报样本信息综合，根据贝叶斯公式得到预报因子的后验信息。贝叶斯方法是与经典统计方法相对应的，贝叶斯学派对于概率的理解上具有主观性，在总体信息和样本信息的基础上还利用了先验信息，而先验信息既可以是客观的，也可以是主观的。在贝叶斯方法中，任何具有不确定量的信息状态均可以用概率的形式来描述，随着新信息的增加，概率可以逐渐得到修正。贝叶斯公式是贝叶斯理论的核心，在天气预报中，对于大雨这一类较强的降雨事件X 的贝叶斯公式可以写为：

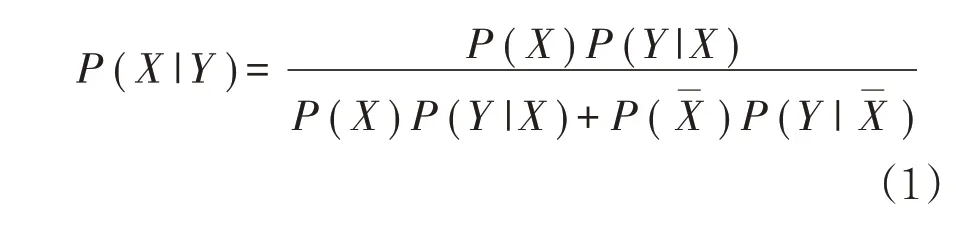
式（1）中，P（Y|X）表示在历史某个给定的时间段内大雨X 发生的概率，称之为似然函数，而P（X）和P（Xˉ）分别表示集合预报未来某个给定的时间段内大雨的发生X 和不发生X 的概率，称之为未知数X 的先验概率，它独立于对历史某个给定时段内大雨发生X 和不发生X 的概率，而后验概率P（X/Y>，即在对历史某个给定时段内大雨发生概率被了解后大雨的发生概率，当然，大雨不发生Y的后验概率P（Xˉ/Y）也可由贝叶斯定理确定。这样，通过贝叶斯方法就将大雨发生的气候概率与集合预报直接输出的>25 mm集合降水概率预报产品结合在了一起，二者的结合实际上就是“压制空报、容忍漏报”的过程，对空报“压制”的基础在于对于某地某一给定时间段内大雨发生的次数是有限的，当大于或等于给定时间段内历史发生最大次数时，大雨再发生的概率就变得很小了，对漏报“容忍”的基础在手，大雨的发生是多种因素的结果，不能要求一种预报指标预报所有的大雨[14]。

2 基于贝叶斯方法的西江流域大雨预报模型

2.1 先验概率的选取

贝叶斯方法首先要确定先验分布，被选取为先验概率的初始因子基本需要掌握以下几条原则：（1）准确率高；（2）简单实用；（3）稳定性好。由于欧洲数值预报中心提供的集合预报效果较好，应用广泛，本文将从欧洲集合预报的结果中获取大雨以上降水的先验概率，对于区域内的一个格点，将某日集合预报成员的降雨量进行计算，输出≥25mm的降水成员占成员总数的百分比作为先验概率，计算公式如下：

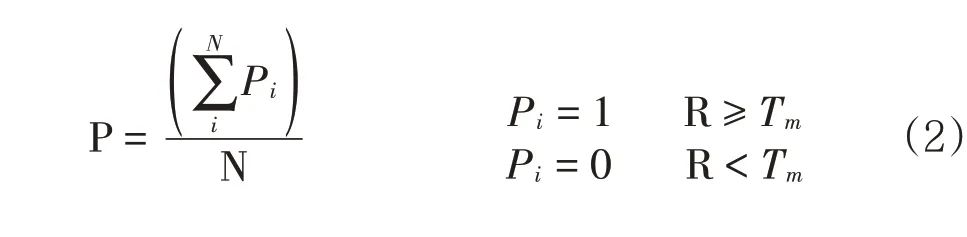
式（2）中，P为大雨降水的先验概率，N表示集合成员数，这里N=51，Pi表示集合成员统计时段内的累积降水量与阈值的比较结果，R 表示每个集合成员的累积预报降水量，Tm表示每个格点对应的雨量阈值，本文取25mm。

2.2 后验概率的计算

在贝叶斯统计方法中，新的信息（或新的统计样本）是通过似然函数进人分析过程的，似然函数就是为了反映新信息（或新样本）而对所考虑事件的先验概率分布所作的修正。客观上似然函数的选取有很多，如何有效地使用似然函数，发挥最佳作用，需要不断地加以探索。根据以往的一些研究[14]，对于强降雨这一类型的事件，其发生与否当月出现的日数有一定关系，可以认为部分符合Bernoulli试验的要求，因而可以用Poisson分布的形式去描述概率特性，故选取研究区域各格点大雨发生当月出现的日数来获取大雨发生的后验概率，当预报格点当月大雨发生次数已经达到或超过月暴雨最多日数，那么该格点当月再发生大雨的概率会减小。具体计算公式如下：

公式（3）中，Λ 为所给定时段大雨日数的平均值，x为预报格点历史上当月已发生大雨次数tr和当月大雨最多日数tm的函数，历史统计时段为1981～2010 年。当预报初始时刻所在月份，tr=0，则a=0，b=0；当预报初始时刻所在月份，tr≠0，则a=1，若1≤tr≤tm且tr＞Λ，则b=1，若1≤tr≤tm且tm＜Λ，则b=0，若tr≥tm则b=-t。

2.3 检验方法

在以上计算方法的基础上，对2016年4～9月的西江流域集合概率预报产品开展了基于贝叶斯方法的修正，并对订正结果进行评估，主要评估方法如下：

（1）TS评分

TS 评分是我国气象预报业务中常用的基于两分类的评分方法，作为对确定性预报的评分标准，已经纳入了业务预报评价体系。TS 评分的计算公式为：

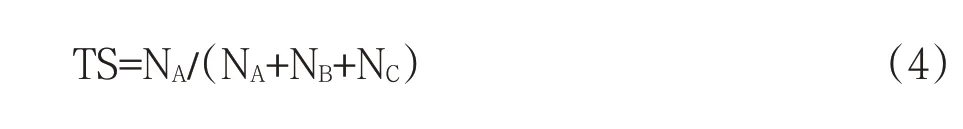
式中NA、NB、NC分别为降水的报对次数、空报次数和漏报次数，TS 值越大表示预报结果越好。对于以上方法计算的大雨后验概率预报，需要转换为确定性预报，通过2016 年4～9 月的后验概率取值≥10%、≥20%、≥30%、≥40%、≥50%、≥60%、≥70%、≥80%、≥90%的阈值，计算各级别的TS 评分值，从结果可知（图略），当概率预报阈值在≥20%时，大雨的TS 评分值最高，故本文采用≥20%的大雨概率预报值进行TS的检验评估。

（2）Brier（BS）评分

Brier 评分定义了一种均方概率误差，该方法综合考虑了可靠性、分辨能力和不确定性。Brier 评分已在定量降水概率预报评估中得到了广泛应用，其具体计算公式为：

式中N为两分类事件的预报数，fi表示某一天气事件发生的预报概率，σi表示实况，事件发生σi为1，事件不发生σi为0，BS 的值在0 和1 之间，BS 值越小越好，BS为1表示评分最差，预报失效。

3 基于贝叶斯方法订正的概率预报性能对比分析

3.1 不同月份不同预报时效的TS评分情况

为了检验贝叶斯方法在汛期不同月份对概率预报的订正效果，计算了2016年4～9月集合概率预报与贝叶斯订正概率预报对西江流域大雨以上降水的不同预报时效的TS 评分情况（图2），从预报评分来看，随着预报时效的增加，各月的预报评分呈逐渐下降的趋势，24～72h 集合概率预报评分总体分别为28～38%、20～37%、20～32%之间；相对应的贝叶斯评分分别为9～41%、7～37%、4～31%，各预报时效贝叶斯方法的低分值月份一律为9 月，该月份的TS评分远低于集合概率预报评分，即贝叶斯方法对9月份西江流域大雨以上的降水基本无有效的订正能力。

在24h 预报时效内，贝叶斯方法4～7 月的预报效果优于集合概率预报，其总体预报评分可提高2～5%，而8月份的预报评分基本一致。对于48h预报时效，贝叶斯方法在4～5月的预报评分相比于集合概率预报可提高约3%，6月份预报评分两者持平，7～8月预报评分略低于集合概率预报1～2%。72h预报时效与48h 预报时效的结果较相似，即贝叶斯评分在4～5月优于集合概率预报，6～8月的预报效果则不如集合概率预报，总体来看，贝叶斯订正方法可以使西江流域前汛期（4～6 月）的大雨以上降水的预报得到有效的提高，在24h 预报时效内也可对后汛期（7～8月）有一定的订正能力，但随着预报时效的延长，其对后汛期的订正效果降低。

图2 集合概率预报与贝叶斯订正概率预报的不同预报时效的TS评分（%）

3.2 不同月份不同预报时效的Brier评分情况

Brier评分是一种负向的评分指数，当Brier分值越低时表示其预报效果越好。计算了2016年4～9月集合概率预报与贝叶斯订正概率预报对西江流域大雨以上降水的不同预报时效的Brier评分情况（图3），在24～72h 预报时效内，集合概率预报的BS 评分总体约为0.026～0.068，贝叶斯方法的BS 评分约为0.019～0.046，贝叶斯方法在4～8 月的BS 评分均优于集合概率预报，即通过订正后的预报产品误差有一定程度的减小，而9 月份的评分低于集合概率预报。在各预报时效内，贝叶斯方法在7 月份的BS 评分效果最好。

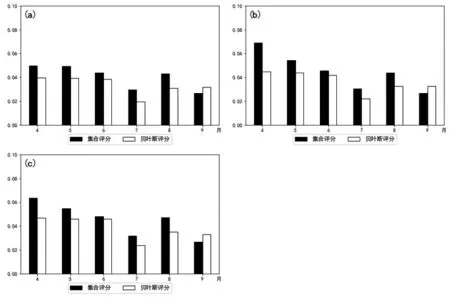
图3 集合概率预报与贝叶斯订正概率预报的不同预报时效的BS评分 （a）24h预报；（b）48h预报；（c）72h预报

3.3 贝叶斯方法订正的前汛期TS评分分布情况

贝叶斯方法对西江流域不同区域的订正性能存在着一定的差异，根据前面的分析，与集合概率预报相比，贝叶斯方法在前汛期有着较好的预报效果，通过计算订正后的24h预报时效内的前汛期（4～6月）的各格点的TS评分，可以了解预报场的空间分布情况（图4，见彩页）。4月份，大雨以上量级预报较好的区域位于西江流域东北部，TS 评分基本≥40%，特别是龙江流域北部、融江流域东部和洛清江部分流域评分可达70～100%；5月份，西江流域评分可达30%以上，预报效果较好的流域为南盘江上游、北盘江下游、郁江、桂东南和沿海流域，TS 评分约为60～100%；6 月份，西江流域评分在40%以上，分值的区域分布较为均匀，评分大于90%的区域范围较小，主要有南盘江下游和桂东南的部分流域。总体来说，随着汛期降水强度和范围的扩大，大部分流域评分增加，但右江和北盘江上游评分较低。

4 结论和讨论

集合数值预报不仅改变了用户的传统观念，也是目前天气预报研究及业务中的热点方向，特别是集合预报系统（EPS）提供的概率预报客观上解决了预报业务中对极端天气不确定因素的判定，得到了各级预报业务人员的广泛认可和普遍应用。本文以贝叶斯概率理论为基础，对集合概率预报产品进行释用，并对其订正前后的结果进行了对比分析。主要结论如下：

（1）TS 评分月际分布情况，在24h 预报时效，贝叶斯订正的概率预报在汛期的大部分时段能够优于集合概率预报，可提升大雨以上量级的预报技巧，随着预报时效的增加，预报性能逐渐减弱，但在前汛期（4～6月）仍有一定的参考作用。

（2）BS 评分月际分布情况，由于贝叶斯订正方法对空报有一定的抑制作用，除了9月份，其他月份在24～72h预报时效内的BS评分均优于集合概率预报，可以在一定程度上减小大雨预报空报的可能性。

（3）区域分布情况，前汛期TS 评分高值区分布存在月际差异，4月至6月随着降水强度和范围的扩大，大部分流域评分逐月提高，但也有部分流域预报技巧难以得到有效的提高。

本文对贝叶斯方法的应用，仅仅采用了集合预报产品中的大雨概率产品与发生当月其出现日数的概率的结合，订正后的概率预报技巧有一定的提高，但是对于个别月份预报性能偏低的原因仍需深入分析，另外，如何运用历史资料构建更加合理的先验概率，从而求取更为精确的订正值，以期更大的提高ECMWF 集合概率预报对西江流域大雨及以上量级降水的预报技巧需做进一步的研究。