基于粒子群算法的电动汽车充电策略研究

熊俊杰，刘 韬，何 昊，黄扬琪，赵伟哲

（1.国网江西省电力有限公司电力科学研究院，江西 南昌 330096；2.国网江西省电力有限公司赣西供电分公司，江西新余338000）

0 前言

家用电动汽车的回归时刻及行驶里程与用户的出行习惯、行驶特点以及电动汽车的充电方式密切相关。大部分的家用电动汽车在常规状态下是一天只充电一次，常规充电所需的充电时间相对较长，而白天车辆大多用于行驶，所以假设家用电动汽车在一天之内最后一次返回停驻地即开始充电。

家庭乘车用户最后一次回到家中的时间主要是集中在15:00-22:00，而且在18:00达到了顶峰。如果按照回家即刻开始满功率充电的假设，对应峰谷分时电价情况，电动汽车具有较大的概率在电价比较高的时间段内进行满功率充电。这对家庭用户来说是十分不经济的，同时也会加剧配电网的峰谷差，对配电网造成不利的影响。假设可以智能控制电动汽车的充电功率，在高峰电价期间充电功率小即电动汽车的充电负荷小，在低谷电价期间充电功率大即电动汽车的充电负荷大，则可以将电动汽车的充电负荷与高电价的时段错开，达到为用户节约电费的目的。智能安排电动汽车的充电功率即是对电动汽车进行有计划有序的充电。

在充电调度和智能充电方法方面，国内外已开展了相关研究，文献[1]提出了基于短期负荷预测降低网损的充电方法；文献[2]优化了电动汽车参与负荷平抑的充放电策略。本文基于机会约束规划建立电动汽车与电网互动调度模型，对充电策略进行优化，并通过算例验证了该模型和算法的可行性和有效性。

1 基于机会约束规划的电动汽车与电网互动调度模型

家庭电动汽车与电网互动的本质是电动汽车接受电网侧的各种激励，从而产生相应的调度互动策略[3]。此后，电网侧也会依据电动汽车的互动响应策略重新制定电价激励策略与负荷调度策略，而电动汽车与电网互动策略从本质上说在电网侧的激励下对每个时刻电动汽车的充电功率进行互动调度控制，从而达到减少配电网峰谷差和用户经济最优化的目的。因此，全电智能家居中电动汽车与电网互动策略的模型基础是电动汽车互动调度控制管理。从数学角度出发，就是一种基于最优的目的，对每个时段的电动汽车充电功率（即决策变量）进行最优化求解。下面提出一个以用户电费最低为最优目标的电动汽车与电网互动调度模型。

公式（1）-（4）中，price（i）表示第i时段电网电价；Pev（i）表示第i时段电动汽车功率；b表示电动汽车开始充电时段；e则表示电动汽车结束充电时段；Pmax是电动汽车最大充电功率；Ec表示电动汽车一天消耗的电能。

该电动汽车与电网互动调度模型是一个多维度线性规划，求解方法多种多样，可以采用单纯形法直接求解该线性规划，也可以采用各种智能算法进行求解。但是传统的互动调度模型中均未考虑电动汽车的随机性，而直接视电动汽车行驶里程、回归时间等随机变量为一个固定常数，这种做法必定影响了模型的实际应用[4]。实际真实情况下的随机变量会导致原互动策略失去最优性，从而导致互动结果不可行。

从家庭用户电动汽车的回归时间与行驶路程等概率分布研究可知，家庭电动汽车充电中很多关键因素：例如开始充电时间（公式（2）中的）和需充电量（公式（3）中Ec）都是随机变量。所以家庭电动汽车互动调度模型中就不可避免的带有随机变量或者是随机参数。而且实时电价（公式（1）中的price（i）作为电网侧价格激励的一种，在电动汽车互动调度策略实施之前是未知的，同样具有着一定的随机性。其概率分布可以简单近似为一种以预测实时电价为中心的均匀分布。目标函数和约束条件中均出现了随机变量，原有的模型不再是简单的线性规划模型，而是不确定规划[5]。在电动汽车与电网互动调度模型中，电动汽车充电功率决策模型具有多维性和多样性，同时带有随机参数，属于不确定规划中的随机规划。

作为一种常用的随机规划处理方法，机会约束规划（ChanceConstraintProgramming，CCP）由Charnrs和Cooper提出，主要是针对约束条件中含有随机变量，且必须在观测到随机变量的实现之前作出决策的情况。考虑到所做决策在不利的情况发生时可能不满足约束条件，而采用一种原则：允许所做决策在一定程度上不满足约束条件，但约束条件成立的概率不小于某一个置信水平。

考虑带有随机参数的数学规划模型：

其中x是一个n维决策向量，ξ是一个随机向量，minf（x，ξ）是目标函数，gj（x，ξ）是随机约束规划。

该数学规划模型是没有完全定义的，因为随机变量ξ使目标函数和约束条件变得不明确。基于该考虑随机变量的数学模型，一种有明确机会约束的规划模型被提出如下：

式中Pr{·}表示ξ事件成立的概率；α和β分别是事先给定的约束条件和目标函数的置信水平。当一个决策向量x是可行的当且仅当事件{gi（x，ξ）≤0，j＝1，2…，p}的概率测度是不小于的。而对于含有随机变量的目标函数，目标函数f（x，ξ）本身也是一个随机变量，这样一定有多个f值，使 Pr{f（x，ξ）≤f}≥β成立。从最小化目标函数观点看，所需要取的目标值是目标函数保证置信水平是β时取的最小值。

采取具有随机性的实时电价作为目标函数中的随机变量，同时考虑原有电动汽车的充电时刻与所需充电能量的随机性，将原有的电动汽车与电网互动调度模型转化为一个机会约束规划模型：

式（7）中的price（i）是目标函数的随机变量，假设其服从简单的均匀分布；t和Ec分别是电动汽车充电时刻和所需充电能量。由于机会约束规划模型是让决策变量的约束条件在某一置信水平上成立。所以将电动汽车只能在充电时刻之后进行充电的约束条件在考虑电动汽车充电时刻的概率分布情况下满足某一置信概率α1成立。电动汽车充电功率累积等于所需充电能量的等式约束成立在所需充电能量为一随机变量的条件下的概率为0，完全无法满足任意大于0的置信水平，所以必须将原先的等式约束进行修改。由于电动汽车动力电池不能进行过充，所以认为电动汽车在充电结束时刻达到额定容量的80%～100%即视为满足原先等式约束，同时这一约束也是在考虑电动汽车所需充电能量的概率分布下满足某一置信水平α2成立的。

2 电动汽车与电网互动调度策略

电动汽车与电网互动调度策略是考虑电动汽车随机变量下的基于机会约束规划的互动调度模型最优解。传统的处理机会约束规划方法是把机会约束规划转化为他们各自的等价类。但是这只在特殊情况下才能做到，当约束条件比较复杂或者存在多个随机变量的情况时，需要采用随机模拟技术处理复杂的机会约束[6]。由于多个随机变量出现在目标函数与约束条件中，因而不能用常规的解析方法来求解，而是引入随机模拟来逼近真实的解。同时，它又是一个多决策变量的优化问题，采用粒子群算法求解优化问题具有良好的鲁棒性[7]。因此，采用基于随机模拟的粒子群算法求解得到电动汽车与电网互动调度策略。

应用随机模拟技术处理基于机会约束规划的互动调度模型中的含有随机变量的目标函数与约束条件的具体方法和步骤如下。

考虑机会约束条件：

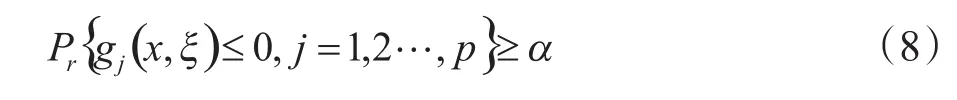
式中ξ是一个随机向量，其累积分布函数为Φ（ξ）。从概率分布Φ（ξ）中产生N个独立的随机变量为ξ1，ξ2，…，ξN。

Step1置N1=0；

Step2从概率分布Φ（ξ）中产生随机变量ξ；

Step3如果满足gj（x，ξ）≤0，j＝1，2，…，p成立，则N1++；

Step4重复Step2和Step3共N次；

Step5如果N1/N＞α，则返回“成立”即认为满足该机会约束条件，否则返回“不成立”即认为不能满足该约束条件。

考虑带有随机参数ξ的目标函数：

式中ξ是一个随机向量，其累积分布函数为Φ（ξ）。

Step1从概率分布Φ（ξ）中产生N个独立的随机变量为ξ1，ξ2，…，ξN；

Step2置fi＝f（x，ξ1），i＝1，2，…，N；

Step3置N1为βN整数部分；

Step4返回序列{f1,f2,…，fN}中第N1个最小的元素；

当含有随机变量的约束条件与目标值得到处理之后，基于机会约束规划的互动调度模型可以进行求解，采取粒子群算法对其进行求解。

粒子群优化算法（ParticleSwarmOptimization，PSO）最初由Kennedy和Eberhart基于一种社会心理学模型中的社会影响和社会学习而提出，是一种基于迭代的优化工具。系统初始化为一组随机解，通过迭代搜寻最优值。每个解被看作是一个粒子，其位置（就是它的值）表示为D维空间中的一个矢量，其速度（就是它下一时刻的位置与当前时刻的位置之差）也表示为一个D维空间中的一个矢量。每个粒子都有一个由被优化的函数决定的适应值（fitness），用于评价该粒子位置的“好坏程度”。每个粒子都能记忆自己移动经验中的最优位置和所有粒子移动经验中的最优位置。粒子每一次根据自己的移动惯性（即自己的当前速度）、个体的最优经验（Pbest）和群体的最优经验（Gbest）来决定自己的速度，并根据决定了的速度更新自己的位置。在达到了一定的迭代步数或者在满足了一定的精度条件之后，所有粒子的所有到过的位置中适应值最优的位置，即为最终求得的最优解。

基本粒子群算法的算法原理如下：

设D维空间中第i个粒子的位置和速度分别为Xi=（xi，1xi，2…xi，d）和 Vi=（vi，1vi，2…vi，d），第 i个粒子的个体最优位置Pbest为Pi=（pi，1pi，2…pi，d），所有粒子中的最优位置Gbest为Pg=（pg，1pg，2… pg，d），则每个粒子通过如下式子来更新各自的速度和位置：

其中为惯性圈因子，c1和c2是正学习因子，r1和r2为0到1之间均匀分布的随机数，j＝1，2，…d。

一般来说，粒子群算法希望在飞行开始时候具有比较好的探索能力，而随着迭代次数增加，特别是飞行的后期，希望具有较好的开发能力，所以希望可以动态调节关系权重。采取线性减小的惯性权重变化方式，设惯性权重取值范围为[wmin，wmax]，最大迭代次数为Iter_max，则第i次迭代时的惯性权重通过公式（12）计算得到：

应用Venter和Sobieszczanski-Sobieski提出的方法处理带约束的粒子群优化问题。算法的基本原理和步骤与公式（10）、（11）中所述的基本粒子群算法相同，只不过在更新粒子的速度和位置时，先通过约束条件判断粒子的当前位置是否是可行的。如果粒子的当前位置可行，则仍通过式（10）更新粒子的速度；如果粒子的当前位置不可行，利用公式（13）硬性将当前位置更改为该粒子最优位置，速度则改用式（14）更新粒子的速度：

这种方法将不可行粒子之前速度的记忆删除，且新的速度只与个体最优位置和群体最优位置有关。这种将速度惯性去除的结果是将不可行粒子被拉回到可行空间。

利用公式（10）至公式（14）描述的算法原理结合随机模拟实现含随机约束的电动汽车与电网互动调度粒子群优化，具体的算法步骤如下：

1）随机初始化粒子种群中各微粒的位置和速度；在种群初始化中，因为带约束的粒子群算法需要一个可行的初始种群。所以在随机产生粒子位置后，对其进行机会约束的验证，如果不满足，重新进行随机初始化直到产生满足机会约束的初始粒子。这就是种群的一个粒子，按同样的方法初始化N个粒子种群；

2）按照随机模拟计算目标值方法评价每个微粒的适应度（即目标值），将当前各微粒的位置和适应值最优值存储在各微粒的Pbest中，将所有Pbest中适应值最优个体的位置和适应值存储于Gbest中；

3）判断粒子的当前位置是否满足约束条件，如满足则用式（10）更新粒子的速度，用式（11）更新粒子位置；如不满足则用式（13）更新粒子的速度。而后用式（14）更新粒子的位置；

4）利用随机模拟方法重新计算每个微粒的适应度。对每个微粒，将其适应值与其经历过的最好位置作比较，如果较好，则将其作为当前的最好位置；

5）比较当前所有 Pbest和 Gbest的值，更新 Gbest；

6）若满足停止条件（通常为预设的运算精度或迭代次数），搜索停止，输出结果；否则返回步骤（3）继续搜索。

3 算例结果与分析

本报选取NissanLEAF家用纯电动汽车进行算例仿真，其额定容量Qr为30kWh，额定充电功率Pr为3.3kW，视额定充电功率为其最大充电功率。设定电动汽车调度时间步长Δt为一小时。充电结束时段e即为一天调度最后时段n。考虑到电动汽车出行规律与计算方便，将一天调度时间设定为早8:00至第二天早8:00；充电时刻这一随机变量的范围是0-24，即0:00-24:00。这里，在进行随机模拟基于充电时刻随机变量概率累积分布函数产生随机数时，将分布在0-8范围（即0:00-8:00时间段）的随机数视为第二天0:00-8:00中的随机数直接带入计算。

此处认为每个时段实时电价曲线服从以该时段预测实时电价为期望前后范围为0.1的均匀分布。图1为本算例的实际实时电价与预测实时电价曲线。

图1 预测实时电价与实际实时电价

对于机会约束条件中置信水平的设置，α1表示在该置信水平上实际充电时刻是晚于电动汽车的的回归时刻，所以α1的设置应该尽量大。而α1的设置间接控制了实际粒子群算法可以计算的决策变量pev（i）的个数，α1值越大，实际决策变量个数越少，所以α1的设置也不应该过小。综合考虑两者，并结合多次仿真结果，建议选取设置为0.8；对于置信水平α2，建议选取0.6；对于置信水平β，一般认为需要在很高的置信水平上计算最优化目标，所以选取β为0.9；粒子群算法的参数如下：种群规模为20，进化代数为300，粒子的速度范围为[0，1]，设惯性权重取值范围为[wmin，wmax]＝[0，4，9]。

种群进化结果见图2，从图2可以看出，目标函数值即用户费用随着进化代数的增加逐渐减小，体现了用户经济性程度越来越高。而且从图中可以看出，粒子群算法的收敛速度很快，只经过8次迭代就将目标函数值从2.8993元减少到2.0894元，这表明采用线性减小的惯性权重变化方式有利于粒子群算法在初期对全局寻优。而且线性减小的惯性权重变化方式也有利于粒子群算法在迭代的后期进行局部寻优。图中显示在迭代后期，目标函数值基本保持不变情况下还可以在第292代后进一步在局部寻优，可进一步减少目标函数值。最终用户费用降低为1.9299元，相比于初代价格减少了33.44%，极大的减少了用户经济费用与电力能耗，有利于家庭电动汽车积极参与到电网的实时电价的激励响应中来。整个粒子群算法在matlab2014a版本中运行时间为250s左右，完全满足电动汽车与电网互动调度对在线调度控制的时间要求。

图2 粒子群算法收敛曲线

图3 电动汽车充电功率与预测实时电价

将最优化的电动汽车充电功率值与电网侧预测实时电价一并展示在图3中。从图3中可以很明显的看出在20:00之前电动汽车并不进行充电，这表明b取值13（即充电时刻为20:00）是使得该机会约束条件在置信水平β为0.8下成立。与此同时，粒子群算法智能调节不同时段电动汽车的充电功率。最优化的电动汽车充电功率在21:00-23:00时段处于一种很低的充电水平，充电功率近似为0。对比预测实时电价，21:00-23:00时段正是预测实时电价高水平时刻，同时对比负荷曲线，21:00-23:00时段也正是负荷曲线峰荷时刻。最优化的电动汽车充电功率在2:00-8:00时段处于一种比较高的充电水平状态。对比预测实时电价，2:00-8:00时段处于预测实时电价低水平时刻，同时负荷曲线也处于其谷荷状态。粒子群算法这种安排调度不仅仅节约了用户经济费用而且可以间接的降低负荷曲线的峰谷差，起到了一定的削峰填谷的作用。需要指明的是，粒子群算法基于随机模拟进行目标值计算并判断机会约束条件是否成立。所以，实际参与随机模拟的是具有均匀分布特性的实际实时电价，其和预测实时电价在走势上大致相同，但是具体数值并不相同。这也是造成充电功率不完全按照在低电价时刻进行大功率充电的原因。

本算例表明基于机会约束规划的家庭电动汽车日前调度模型可以很好的让家庭电动汽车参与到电网的互动中，积极地响应了电网侧的价格激励，达到了用户费用与电力能源最优化的目的。与此同时，本算例结果也验证了电动汽车调度策略具有一定的削峰填谷的作用，可以有效的帮助电网保持稳定。

4 总结

针对家用电动汽车日常充电行为特性，本文在电网的价格激励条件下提出一种以电动汽车电费最小为目标函数的基于随机模拟的机会约束规划日前家用电动汽车调度策略模型。所提机会约束规划建立在电动汽车的回归时间与行驶路程等概率分布基础上，区别于之前很多的家庭用户的确定性电动汽车互动调度策略，其充分考虑了家用电动汽车的回归时间与行驶距离等随机变量的概率分布情况。所提出的机会约束规划可以应对家用电动汽车所具有的随机性，鲁棒性较强。

算例分析证实了基于机会约束规划的调度策略可以很好的响应电网侧的价格激励条件，减少用户的电动汽车费用。同时，算例也展示了该模型对家庭负荷曲线具有很好的削峰填谷的作用。随着家庭电动汽车的大力推广，由于电动汽车充电负荷特有的随机性与调度转移的便利性，相比于其它家庭负荷设备，电动汽车在智能家居与电网互动中占有重要地位，能更加快速有效针对电网侧的各种激励提出互动策略。本文提出的充电优化方法在不影响电动汽车的使用和不违背电动汽车使用舒适度的情况下降低了电动汽车的电费，达到了电动汽车的经济性与舒适性同时最优的目标。