基于偏相关-灰色综合关联度的温度测点优化*

孟祥忠

(大连职业技术学院，辽宁 大连 116035)

0 引言

数控机床越来越向着高精度的方向发展，在影响其加工精度的所有误差因素当中，热误差逐渐成为主要的影响因素[1-2]。文献[3]指出，目前机床的热误差往往能占到其总误差的40%～80%，而且越是精密的机床，该比例越大。为了解决该难题，提高机床的加工精度，数控机床热误差补偿与建模技术逐渐发展起来，并被证明是一种经济有效的减小机床误差的方法[4]。这种技术的关键是建立整机温度场与主轴热误差之间的函数关系，亦即热误差模型，而模型的预测精度及鲁棒性[5]则直接决定着补偿效果的好坏。机床温度场的获取是通过布置大量温度传感器来实现的，但将全部测点用于建模会大大降低模型的鲁棒性，有时甚至是无法实现的。因此，在热误差模型建立和补偿之前，需要对机床的各热源点进行测点优化，筛选出影响机床主轴热误差的关键测点，从而以较少的，同时与热误差具有明显相关性的测点建立补偿预测模型。

近年来，国内外学者对数控机床的热误差补偿与建模技术进行了深入研究，并取得了丰硕的成果。在温度测点优化技术方面，提出了许多相关理论和方法。闫嘉钰等[6]提出一种基于灰色综合关联度算法的温度测点优化方法，对机床表面的不同测点进行了分组优化；凡志磊等[7]提出一种基于偏相关分析的优化方法，其优点在于避免了温度变量间的相互影响；沈金华等[8]基于聚类分析法，对各温度变量进行分类，再分别从每一类中筛选出具有明显相关性的测点，也收到了良好的优化效果。上述各方法的优化判定指标单一，易形成误判，导致预测模型鲁棒性不佳。Ma等[9]对机床温度场与热误差间的动态特性进行详细分析，从微观的角度对温度测点的位置进行了优化；Min[10]，Zhao[11]，Creighton[12]等基于有限单元法，全面分析了机床温度场与热变形间的关系。由于很难准确获取机床各零部件间的微观关系，因此上述各方法的优化结果并不理想。

在前人研究成果的基础上，本文采用多种理论相结合的方法，引入多个优化评价指标，综合考虑温度测点间、温度测点与热误差间的相关性，以提高优化结果的准确性及预测模型的鲁棒性。采用偏相关分析的方法，控制多个温度变量间的相互影响，筛选出来与热误差具有相关性且通过了假设检验的温度测点。对初步筛选出的测点进行基于灰色理论的综合关联度分析，量化各测点对热误差的影响程度。最终，优化得到用于主轴Z向热误差建模的关键测点，同时对优化结果的准确性进行了实验分析。

1 相关理论分析

1.1 偏相关分析

简单相关性分析是统计方法的一种，它用来研究各变量间的相关关系，一般用简单相关系数rxy来表征变量x，y之间的关联程度，计算公式：

(1)

简单相关理论一般用于分析两个变量间的相互关系，它忽略了其他变量对这两个变量的影响。因此，当研究对象仅有两个变量时，用简单相关系数来表征其线性相关程度是可行且准确的；但当研究对象是多个变量时，若仍然使用简单相关分析，那么得出的结论往往具有虚假性。为了能够准确地反映出多变量之间的相关性，这里有必要引入偏相关性分析方法[7]。

设一组变量x1，x2，…，xn，则由简单相关系数rij组成的相关矩阵R：

(2)

对矩阵R求逆：

(3)

则可求得xi和xj间的偏相关系数：

(4)

1.2 灰色综合关联度分析

相对于整机温度场，所采集的温度数据具有小样本、贫信息的特点，而采用灰色系统分析则能较好地解决该问题。灰色关联度分析方法一般有绝对和相对两种，在此基础上发展起来的灰色综合关联度分析法，结合了两者的特点，更能准确的反映出因素间的关联度情况。

设Xj={xj(1)，xj(2)，…，xj(n)}为系统行为序列，记热误差序列为X0，温度测点i的序列为Xi，ε0i和r0i分别为两序列X0和Xi的绝对关联度和相对关联度，定义：

ρ0i=θε0i+(1-θ)r0i

(5)

为Xo和Xi的灰色综合关联度。θ[0,1]用来调整相对关联度和绝对关联度相对于综合关联度的影响程度，一般取θ=0.5。

2 温度测点优化方法的实施

2.1 实验分析

如图1所示，以某机床厂生产的卧式加工中心为研究对象，在对其温度场分布及热动态特性分析的基础上，在热源附近分别布置16个温度传感器，每个传感器经过特殊处理，以保证都能可靠的粘贴在机床表面，其安装位置如表1所示。通过电涡流位移传感器来采集机床主轴的Z向热误差，传感器的安装位置及布置方式如图2所示。实验数据的采集在空切削方式下进行，为尽量模拟实际工况，机床的运行方式设置如表2所示。

图1 温度传感器的位置布置

编号安装位置编号安装位置T1主轴箱上侧轴承(前)附近T9主轴端面(前)T2主轴箱上侧轴承(后)附近T10主轴端面(后)T3电机(Y)表面T11环境温度T4近机端轴承表面(X)T12远机端轴承表面(X)T5电机(Y)表面T13远机端轴承表面(Y)T6主轴表面(前)T14立柱滑块表面T7主轴表面(中)T15主轴箱下部轴承附近(后)T8主轴表面(后)T16主轴箱下部轴承附近(前)

图2 主轴Z向位移传感器的安装位置

主轴转速(r/min)进给速度(mm/min)运行时间(min)20003035003045001500030350030200030

2.2 测点优化结果

由实验数据，首先计算各温度测点与主轴Z向热误差间的偏相关系数，并采用t统计量对其进行双侧检验，检验水平a=0.05，结果如表3所示。表中:ΔTi(i=1,2,…，16)表示相对于初始环境温度的变化量。

表3 各温度测点与热误差间的偏相关性

由表3可知，多数的温度变量与热误差具有相关性，但通过检验的只有ΔT2、ΔT3、ΔT4、ΔT5、ΔT9、ΔT13、ΔT15，说明部分温度测点对热误差的影响带有欺骗性。

对通过检验的温度测点采用基于灰色综合关联度的分析方法，以主轴的Z向热误差为母序列x0，7个温度测点变量为子序列xi(i=1,2,…，7)，计算各子序列与母序列间的灰色综合关联度数值，计算结果如下：

r0,2=0.6791r0,3=0.7237
r0,4=0.7575r0,5=0.6423
r0.9=0.6325r0.3=0.7430
r0.15=0.6329

温度测点的灰色综合关联度值越大，说明其与母序列的关联度就越紧密，即越能反映出主轴Z向热误差的变化规律。由此，对温度测点进行筛选：ΔT2、ΔT3、ΔT4、ΔT13，如图3所示，这即为该机床的4个关键温度测点。

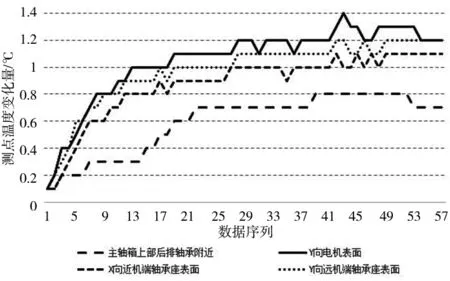
图3 关键温度测点数据

3 实验验证

首先分析热误差与关键测点间的线性相关性，如表4所示。

表4 简单相关分析结果

可以看出，热误差与关键温度测点间的线性相关性不明显，且均未通过假设检验，因此，无法直接采用多元线性回归的方法建模。BP神经网络具有良好的非线性映射特点，同时具备较强的数据并行处理、容错、存储等能力，因此，这里采用BP神经网络算法对优化结果进行实验分析。

以优化得到的4个关键测点作为BP神经网络的输入，机床主轴的Z向热误差作为输出，建立热误差预测模型(记为：模型P-H)，如图4所示。

图4 模型P-H的热误差预测图

采用同样的思路，建立基于偏相关分析的测点优化方法，得到4个关键温度测点：ΔT2、ΔT5、ΔT9、ΔT13。以这4个测点为输入变量，建立基于BP神经网络的热误差预测模型(模型参数设置同上，记为：模型P)，如图5所示。

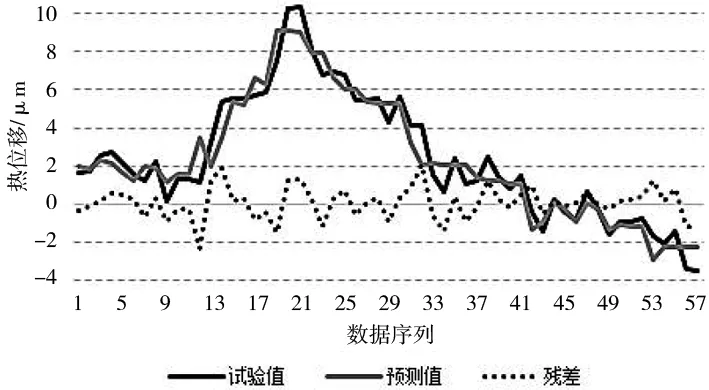
图5 模型P的热误差预测图

采用同样的思路，建立基于灰色综合关联度的测点优化方法，得到4个关键温度测点：ΔT1、ΔT3、ΔT4、ΔT13。以这4个测点为输入变量，建立基于BP神经网络的热误差预测模型(模型参数设置同上，记为：模型H)，如图6所示。

图6 模型H的热误差预测图

分析以上3种热误差模型的预测精度，以最大残差、平均残差、标准差来综合表征，如表5所示。

表5 热误差预测模型结果

从表5可以看出，采用本文方法建立的热误差模型，其最大残差1.299μm，平均残差0.594μm，预测效果明显优于其他两种方法。此外，通过标准差可以看出，采用本文方法得到的预测数据相对于真实数据的离散程度要大大小于其他两种方法。

4 结论

机床的温度测点优化是进行热误差建模与补偿的重要前提，本文采用多种理论相结合的方法，通过合理引入多个优化评价指标，综合考虑温度测点间、温度测点与热误差间的相关性，提高了优化结果的准确性及预测模型的鲁棒性。

(1)提出了一种基于偏相关-灰色综合关联度的数控机床温度测点优化算法，测点数量由原来的16个减少至4个。根据优化结果，建立了4测点的热误差预测模型，分析表明，主轴Z向最大热误差由10.338μm减小至1.299μm，验证了该方法的有效性。

(2)对比分析了本文方法和另外两种测点优化方法，结果表明：采用本文方法建立的模型的预测精度明显优于该两种方法，其最大残差1.299μm，平均残差0.594μm，且预测数据的离散程度也达到了最小。

(3)机床的热误差补偿技术是一项系统工程，获取关键温度测点之后，需要合理选择和设计补偿模型和补偿控制器，从而真正意义上实现在线补偿，提高机床的加工精度。