基于BP神经网络的船舶航向智能PID控制研究

李小峰，于慧彬

(齐鲁工业大学(山东省科学院)，山东省科学院海洋仪器仪表研究所，山东省海洋监测仪器装备技术重点实验室，国家海洋监测设备工程技术研究中心，山东 青岛 266001)

船舶航向控制是船舶航行操纵的重要组成部分，其性能的优劣决定了航行的安全性和经济性，船舶航向控制系统是船舶的关键设备之一。船舶航向运动模型是一种典型非线性时变系统，为便于进行控制系统设计，在船舶航行保持阶段可将此运动模型进行简化，用一阶KT模型对船舶航向运动进行描述，这种传统PID控制系统结构简单，易于实现[1]。对于船舶航向运动这种大惯性系统而言，控制系统的稳定性是系统设计时需重点考虑的问题。常规的自适应算法参数整定困难，一般都是凭借操作人员的经验，根据驾驶船舶的航速、海况、船舶装载情况以及船体吃水等诸多因素，进行人工航向调整，缺乏对船舶动态及海况变化的自适应能力，易受主观人为因素的影响。由于船舶自身的非线性特性，控制效果与稳定性难以保证。

为改善上述传统控制系统的局限性,本文利用BP神经网络自身具备的良好逼近非线性系统的能力，再结合传统的PID船舶控制理论，针对某型渡轮航行时的航向特性，设计了基于BP神经网络的自适应控制策略。运用神经网络的自学习能力，辨识出PDI控制系统所需的三个关键参数，通过动态调整控制参数并优化神经网络的收敛速度，实现自整定的PID控制器，在MATLAB/Simulink环境下对所设计系统的性能进行了软件仿真验证。

1 船舶运动数学模型

对于直线稳定的船舶，根据一阶KT方程描述出的船舶操纵运动响应能够满意地逼近船舶的实际运动。为达到工程应用的要求，将一阶KT方程用于船舶控制系统控制器的设计中，把船舶整体看成刚体，并假定船舶在回转时只受到转艇时受到的力矩和水的阻力力矩的作用，船舶舵机采用下式模型表示：

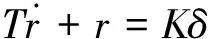
(1)

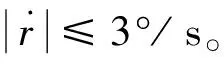
2 传统航向控制原理

航向控制系统是一种典型的自动控制系统，系统以船舶航向角为控制对象，接收电罗经等航向测量设备输出的船舶航向信号、舵角反馈机构反馈的舵角信号、航向指令设定信号等输入信号，经过航向控制系统综合运算给出指令舵角信号，并控制舵机转动，实现对船舶航向的有效控制。PID控制属于线性控制方法，传统PID控制系统原理如图1所示[3]。根据航向操作给定指令r(t)与实际舵机输出值y(t)构成的方向控制偏差e(t)，对实际输出与预设值之间的差值分别进行积分运算、比例运算及微分运算，然后将前述各个运算结果相加，如图所示，即可得到对船舶舵机的控制输出结果u(t)，并将该结果输出到舵机。反复此过程实现对船舶航向的控制。

图1 PID控制系统原理框图Fig.1 Principle block diagram of PID control system

传统航向PID控制器的输入输出关系为：

(2)

式中,u(t)为输出值，e(t)为取样偏差值，即e(t)=r(t)-y(t)；Kp为比例系数，Ti为积分时间常数；Td为微分时间常数[4]。

3 船舶航向智能PID控制器设计

根据传统PID(proportion(比例)-integral(积分)-derivative(微分))系统控制理论，需要调配PID控制系统中积分、微分以及比例运算三个环节的控制作用，使各运算环节相互制约又相互配合。三种运算环节不能仅仅进行简单的线性组合叠加，而是需要在各种多样化的非线性组合中找出符合实际船舶操控的最佳组合方式[5]。神经网络在处理非线性函数时具有极强的逼近能力，同时自身还具备自学习能力，依据船舶的实际参数情况设定最优指标，神经网络能够学习船舶航向操纵控制系统的反馈结果，根据反馈情况自动调整神经网络系统内部的设计参数，重复此过程直至控制结果达到航向PID控制的预设误差要求范围内为止。使PID控制器能够快速响应船舶结构、相关运行参数以及输入信号的变换，并在有外界扰动输入时能够抵御其对控制系统的影响。应用BP神经网络理论，设计基于船舶控制参数Kd、Ki、Kp的具有自学习能力的PID控制器[6]。

基于BP网络设计的具备自学习能力的PID控制系统结构框图如图2所示。该控制系统以传统经典PID控制系统为基础，经典PID船舶航向控制器直接对舵机进行闭环控制，系统内3个主要参数：积分系数Ki、微分系数Kd及比例系数Kp均为在线调整方式。在该基础上设计增加BP神经网络控制单元，该单元将接收系统的运行状态，结果自学习后输出用于Kp、Ki、Kd这三个用于航向控制调整的参数到PID控制器中作为控制器的输入。通过BP神经网络的自学习及加权调整，使输出参数对应于预设工况情景下的最优控制PID参数[7]。

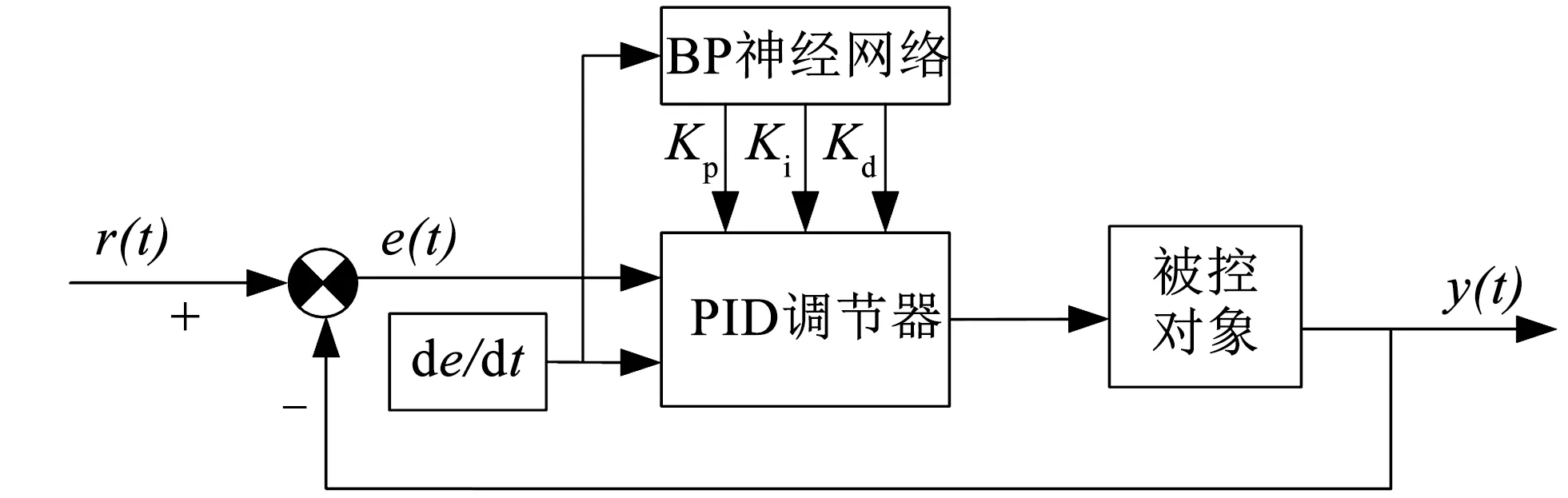
图2 基于BP神经网络的航向PID控制系统原理框图Fig.2 PID control system block diagram based on BP neural network

经典的PID控制器算法我们采用增量式数字PID控制算法，该算法在控制过程中每次输出的控制值仅是控制的增量，执行器每次变化量较小，被控对象参数变化平缓，控制系统相对稳定。其控制算法公式为：

u(k)=u(k-1)+Δu(k)，

(3)

式中，Δu(k)为PID控制器第k次相对于第(k-1)次控制量的增量，即

Δu(k)=Kp(e(k)-e(k-1))+Kie(k)+Kd(e(k)-2e(k-1)+e(k-2))。

(4)

认为Kp、Ki、Kd为随系统运行状态的可调系数，则有：

u(k)=f[u(k-1),Kp,Ki,Kd,e(k)],

(5)

即u(k)是与u(k-1),y(k),Kp,Ki,Kd相关的非线性函数，可通过样本训练，利用BP神经网络获得最优解，从而得到船舶航向控制的最优控制系统。

此次的BP神经网络设计采用结构如图3所示的三层BP网络结构。网络分为输入层、隐含层与输出层三层。其中，输入层设置有输入节点M个，隐含层设置有运算节点N个，输出层设置有网络节点Q个。船舶航行控制系统的运行状态数据通过输入节点录入神经网络，数据在输入神经网络时需预先进行归一化处理。设计BP神经网络的输出节点分别对应于PID航向控制系统的调节参数Ki、Kd、Kp。考虑到航向PID控制系统中上述三个参数的取值范围均不能为负，因此在输出层神经元激活函数设计时，该函数设计选取非负的Sigmoid函数。对于BP神经网络隐含层神经元激活函数，在设计时则相应地选取了正负对称的Sigmoid函数[8]。

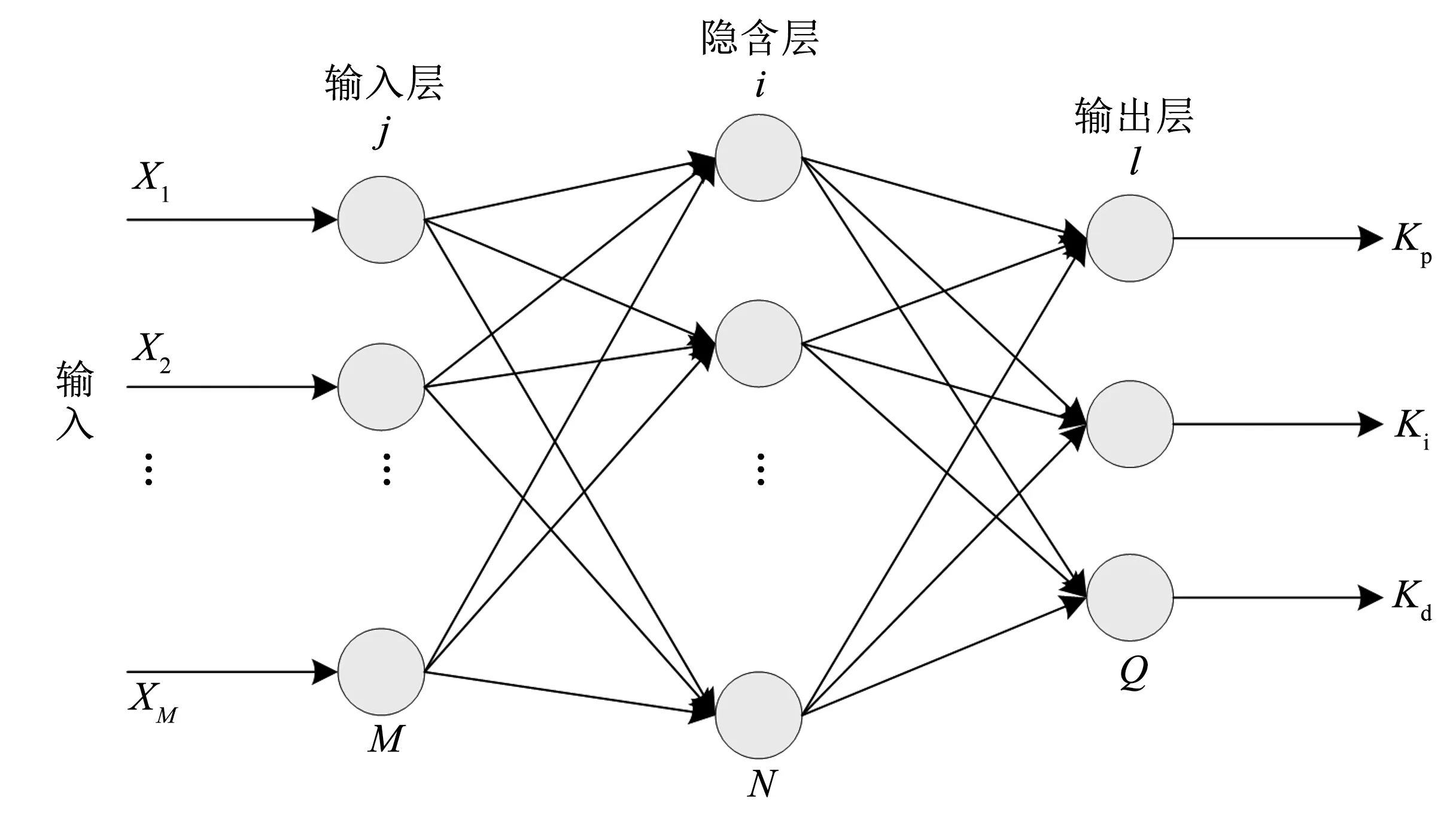
图3 BP神经网络单元组成结构图Fig.3 Structure diagram of BP neural network unit

由BP神经网络单元组成结构图可知，输入层为：Oj=Xj,j=1,2,3，…,M，其中，Oj为输入层第j个节点的输出，输入节点的数量M取决于被控系统的复杂程度。

网络隐含层的输入输出为：

(6)

式中,φ(k)为神经网络某一层的输入函数；上标 (1)，(2)，(3)分别代表神经网络的输入层、隐含层及输出层；ωij(2)为神经网络隐含层加权系数，θi(2)为神经网络隐含层神经元阈值函数；f[x]为神经网络隐含层神经元激活函数，如前所述取正负对称的Sigmoid函数。即：

f[x]=tanh(x)=(ex-e-x)/(ex+e-x)。

(7)

BP神经网络输出层的输入输出为：

(8)

。

(9)

BP神经网络的性能指标函数则设计选取为：

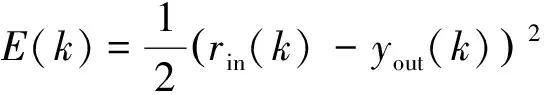
(10)

其中，rin(k)为期望输出，yout(k)为实际输出。为能够快速获得自学习结果，设计采用梯度下降法来修正BP神经网络的加权系数。将E(k)对加权系数的负梯度方向设定为该法的搜索方向，考虑到该方法越接近目标值，步长越小，收敛速度越慢，故设置一个使搜索快速收敛的全局极小的常数阈值，则有：

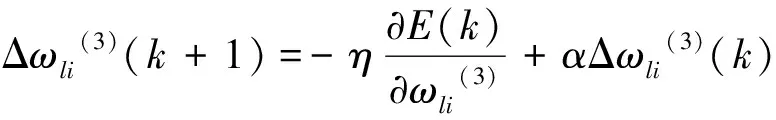
(11)

其中，η为学习速率，η>0，α为惯性系数，其通常取值范围在0～1之间[9]。

。

(12)

其中

(13)

。

(14)

。

(15)

由以上各式可推导BP神经网络输出层的加权系数计算公式为：

(16)

BP神经网络隐含层加权系数的计算公式可参考前述输出层的推导过程，进行推算可得：

(17)

4 仿真实验

仿真结果如图5所示，Kp、Ki、Kd的变化趋势如图6所示。从图中可以看出，基于BP神经网络的PID控制器可以实现舵的实时控制，使船舶航向角跟踪上给定值，只要预定航向角实时航向角存在误差，舵机就能不断工作，直至误差为零，此时舵角归零。航向角在约100 s时有外界干扰介入，舵角一开始迅速下降，之后迅速上升，最后舵角误差归零，船舶达到预定航向角。系统的超调很小，鲁棒性好，可以长时间稳定工作，稳态误差可控。从仿真结果看，与周蓉[3]、霍星星等[8]、彭秀艳等[9]在该领域进行实验取得的相关仿真结果一致，表明该方法应用到实船工程设计中后，可以有效减少船舶舵机的损耗。

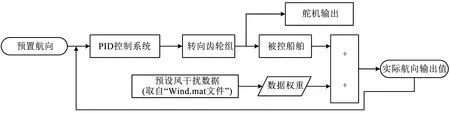
图4 船舶航向控制系统仿真框图[10]Fig.4 Simulation diagram of ship course control system [10]

图5 航向变化图Fig.5 Vessel heading curve

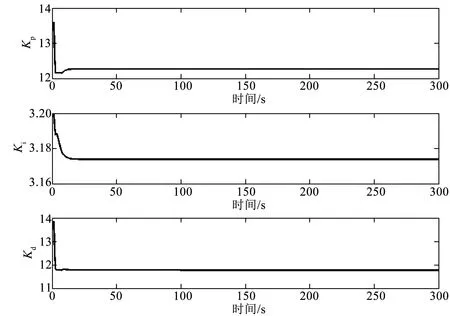
图6 Kp，Ki，Kd变化图Fig.6 Kp，Ki，Kd curve

5 结语

本文针对船舶航向运动特性建立了基于一阶KT模型的船舶航向控制系统模型，根据航向控制系统特性给出基于BP神经网络的PID控制参数的训练获取方法。控制系统设计完成后，根据真实渡轮船舶特征参数，利用MATLAB/Simulink仿真软件建立船舶航向运动控制系统模型并进行航向控制仿真模拟运算。仿真结果表明，基于BP神经网络的PID航向控制系统具有自学习能力，超调小、鲁棒性好，控制系统可长时间稳定工作，几乎无稳态误差。仿真结果显示设计的船舶航向控制系统实现了对船舶航向的有效控制，证明基于BP神经网络的PID控制算法对船舶航向控制的有效性。由于BP神经网络自学习速度不够迅速，收敛速度还需要调整，虽然仿真结构较为理想，但在仿真时没有考虑加入海浪对控制的影响，这与实际航向环境也有较大差距，需在今后进一步地加以研究。目前此项工作还处在仿真实验阶段,并未真正应用于船舶舵机设备，随着算法研究的不断深入和提高，以及神经网络方法的日趋完善，该设计方法将能够通过硬件设计应用于船舶自动舵设备中，未来将具有广阔的应用前景。