锥盘底和平底搅拌槽固液混合特性的CFD研究

2018-08-28贾慧灵任保根

机械设计与制造 2018年8期

贾慧灵，赵静，李梅，任保根

1 引言

固液混合是搅拌技术中比较常见的一种操作，广泛应用于结晶、冶金和催化等工业反应过程[1]。反应原料的混合程度直接影响产品的质量，搅拌槽的底部形状是影响混合效果的关键因素之一。文献[2]用实验研究了平底搅拌槽和锥盘底搅拌槽的完全离底悬浮和淤桨悬浮，发现这两种悬浮中平底的效率较低。实验研究通常受到物理模型和检测技术的限制[3]，所以更多的研究者利用计算流体力学（CFD）来研究搅拌槽底部的速度和浓度分布。2002年，文献[4]用CFD研究了固液平底搅拌槽内的速度分布，当有固体颗粒加入时，槽底中心的倒锥形区域比无固体颗粒时的大，全槽主体循环的流体量减小。文献[5]使用CFD对固液平底搅拌槽槽底流场进行研究，发现靠近槽中心和边缘区域的液相速度比较小，固体颗粒浓度较大。由于平底搅拌槽中的循环流不能到达槽底中央和槽底与槽壁的交接处，故在这两个部位易产生固体颗粒的沉积。所以对平底搅拌槽的底部结构进行了改进，利用CFD软件分别对改进后的锥盘底搅拌槽和平底搅拌槽内浓度场进行了对比研究，分析了搅拌槽底部形状对固液混合时间、搅拌功率、湍动能和固相速度的影响，为工业中固液搅拌槽底部形状的选取提供理论依据。

2 几何模型

选取的研究对象为锥盘底圆柱形搅拌槽，如图1（a）所示。平底圆柱形搅拌槽，如图1（b）所示。两个底部结构不同的搅拌槽的直径为T=150mm，高度为H=T，选用45°圆盘涡轮式搅拌桨，搅拌桨安装高度为C=T/3=50mm，搅拌桨宽度为w=10mm，挡板宽度为B=T/10=15mm，浓度检测点分别取上部P1、桨叶平面P2和底部P3。以搅拌桨中心为坐标原点，建立的圆柱坐标系，如图1所示。

分析可知搅拌槽底部中心处和搅拌槽槽壁与槽底的交接处速度很小，使得固体颗粒容易在此处堆积，不利于搅拌混合。所以将槽底中心处去掉一个直径为0.3D、高为0.2D的圆锥体，将搅拌槽槽壁与槽底的交接处减去一个截面为等边直角三角形的回转体，三角形的直边长为0.15D，如图1（a）所示。

图1 搅拌槽几何模型Fig.1 Geometry Model of Stirred Tank

3 模拟方法

使用软件Fluent14.5进行模拟计算，浓度场计算采用欧拉-欧拉多相流模型[6-7]，选用标准的k-ε湍流模型[8]，方程见式（1）和（2）。搅拌桨的转速为300r/min。将计算域分为运区和静区。旋转的搅拌桨处于动区，其它结构均在静区，动静区域的交互作用采用多重参考系（MRF）[9]，动静区交界面上的参数通过连续性方程式（3）、动量方程式（4）和能量方程式（5）进行传递。

式中：μl—层流黏性系数；μt—湍流黏性系数Gk—层流速度梯度产生的湍动能；Gb—浮力产生的湍动能；σk、σε、C1、C2和 C3—经验常数；μ—有效黏性系数 μ=μl+μt。

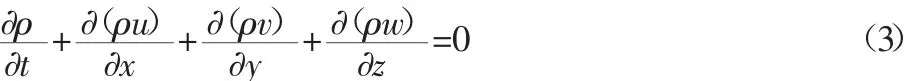
式中：ρ—密度；t—时间；u、v和w—速度矢量在x、y和z方向的分量。

式中：p—微元体上的压力；τxx、τyx和 τzx—作用在微元体表面上的黏性应力的分量；Fx、Fy和Fz—微元体上的体积力。

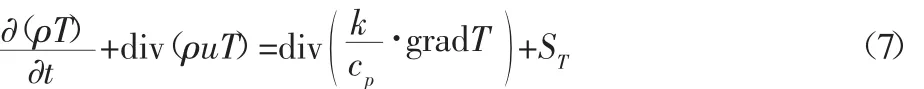
式中：cp—比热；T—温度；k—流体的传热系数；ST—流体的内热源。

3.1 模拟物系

固液两相流中液相为水，密度998.2kg/m3，粘度0.001003Pa·s；固相为碳酸铈晶体颗粒，密度2350kg/m3，粘度0.0055Pa·s，碳酸铈颗粒直径为10μm，体积分数为10%。由于碳酸铈体积分数比较高，固液相间曳力系数采用schiller-naumann模型[10]。采用SIMPLE算法进行求解，时间步长取为0.005s，收敛残差设为（1×10-4）。

3.2 实验验证

为了与文献[11-12]的实验数据进行比较，模拟所采用的搅拌槽结构与其实验装置一致，即将搅拌槽直径改为270mm，45°圆盘涡轮式搅拌桨改为90°圆盘涡轮式搅拌桨，搅拌桨宽度w改为18mm。考察搅拌桨宽度处的湍动能k随轴向位置的变化，并与实验结果[11-12]进行对比，如图2所示。图中：Vtip—搅拌桨尖端的线速度，在搅拌桨上下两端的模拟值与实验值比较接近，在中间部位的模拟值约为实验值的50%，文献[13]对此模型搅拌桨宽度处的湍动能也进行了CFD模拟，其值较接近此处的模拟值，但此处的模拟结果更接近实验值。

4 模拟结果与分析

4.1 固相浓度变化图

锥盘底和平底两种结构搅拌槽不同时刻下的固相浓度的分布云图，如图3所示。浓度值为1代表全部为碳酸铈颗粒，为0代表不含固体颗粒。从图中可以看出，初始0时刻至1s，固体颗粒沿轴线方向向上运动，搅拌槽底部固体颗粒明显扩散，锥盘底搅拌槽中，固体颗粒已经扩散到搅拌桨的上部，而平底搅拌槽中只扩散到搅拌桨区域。2s时，底部的固体颗粒继续向搅拌槽的上半部扩散，锥盘底搅拌槽底部的固相浓度明显减小，而平底搅拌槽固相颗粒刚开始沿槽壁向上部扩散。随后在3s时，锥盘底搅拌槽中的固相颗粒几乎充满整个搅拌槽，平底搅拌槽中的固相颗粒刚运动到搅拌槽中部。最后在28s时锥盘底搅拌槽中的固相浓度分布基本不变，达到平衡状态，而平底搅拌槽在36s才达到平衡。

图3 不同时刻下固相浓度的分布云图Fig.3 Contours of Solid Phase Concentration at Different Moments

4.2 混合时间

图4 两种结构搅拌槽的混合时间Fig.4 Mixing Time of Stirred Tank with Two Structures

混合时间T是固相浓度从开始到稳定浓度值的±95%所用的时间。两种结构搅拌槽中3个监测点的混合时间曲线，如图4所示。从监测点1看出，锥盘底搅拌槽的固体颗粒浓度在初始阶段比平底搅拌槽的高，虽然平底搅拌槽内的固体颗粒浓度在4s开始升高，锥盘底搅拌槽在6s才有所升高，但是通过斜率可以看出锥盘底搅拌槽内的固体颗粒浓度的上升速度更快，到达平衡时的时间较短。在监测点2处，平盘底搅拌槽的固体颗粒浓度在初始阶段比锥盘底搅拌槽的高，但平底搅拌槽的波动较小，在5s时锥盘底搅拌槽的固体颗粒浓度迅速上升超过平底搅拌槽，很快达到平衡。从监测点3看出，两种结构搅拌槽的固体颗粒浓度都是先升高后降低，这是由于沉于底部的固体颗粒随着搅拌桨的转动向上运动，使得该处的浓度先升高，而后固体颗粒逐渐向上部扩散，使得该处浓度下降，在28s时，锥盘底搅拌槽的固体颗粒浓度超过平底搅拌槽，较早达到平衡，平底搅拌槽在36s才达到平衡。

4.3 搅拌功率

搅拌功率是指搅拌桨以一定的转速进行搅拌时，对流体做功并使之发生流动所需要的功率[1]。搅拌功率P的计算如式（8）：

式中：M—搅拌扭矩；为搅拌轴旋转角速度；N—搅拌轴旋转速度。

两种结构搅拌槽的搅拌功率的计算结果，如表1所示。

表1 两种结构搅拌槽的搅拌功率Tab.1 Mixing Power Stirred Tank with Two Structures

从表1中可以看出平底搅拌槽的搅拌功率仅比锥盘底搅拌槽的搅拌功率小1.6%，可以近似认为两种结构搅拌槽所需搅拌功率相同，所以搅拌槽的底部形状对搅拌功率的影响不大。

4.4 湍动能k

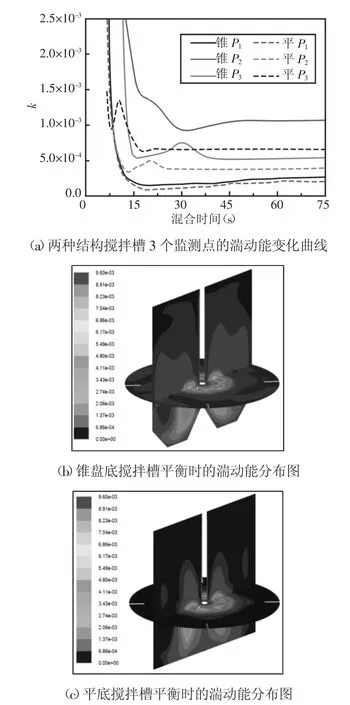
图5 湍动能变化图Fig.5 Variation of Turbulent Kinetic Energy

湍动能变化图，如图5所示。两种结构搅拌槽中3个监测点处的湍动能变化曲线图，如图5（a）所示。从图5（a）中可以看出锥盘底搅拌槽中3个监测点的湍动能都大于相应的平底搅拌槽的，并且湍动能达平衡时间都比平底搅拌槽时间短。这是由于锥盘底搅拌槽底部的锥状结构消除了搅拌时循环流不能到达的搅拌槽槽底中央和搅拌槽槽底与槽壁的交接处，流体流动时的方向转折比平底搅拌槽中的要剧烈，使得底部循环流与槽底和槽壁的碰撞次数增多，增大了湍动能，湍动能的增大促进固液混合的效果，缩短了混合时间。锥盘底和平底搅拌槽达平衡时的湍动能云图，如图5（b）、图5（c）所示。两种搅拌槽的湍动能都主要集中在搅拌桨附近，最小值均出现在挡板背部。从横向图看，在搅拌桨区域，锥盘底图5（b）中最大湍动能出现的区域比平底图5（c）中出现的范围更大。图（b）中搅拌桨和搅拌槽壁之间有较大的湍动能分布，而图5（c）中此区域的湍动能几乎为0。从轴向图5（b）中可以看出，锥盘底搅拌槽中的湍动能已经到达搅拌槽的中部，搅拌槽槽底与槽壁的交接处也分布有湍动能。而平底搅拌槽（轴向图5（c））的湍动能只在搅拌桨区域，而且搅拌槽的槽底与槽壁的交接处几乎没有湍动能分布。可见锥盘底搅拌槽的湍动能分布比平底搅拌槽的更有利于固液两相间的混合。

4.5 固相速度

两种结构搅拌槽中3个监测点的固相速度速随时间的变化曲线，如图6所示。固相速度越大，越有利于固液相间的接触与混合。从图6中可以看出，锥盘底搅拌槽的P1和P2监测点的固相速度都和相应的平底搅拌槽的固相速度比较接近，但是锥盘底搅拌槽的P3监测点的固相速度比相应的平底搅拌槽的大，这是由于锥盘底搅拌槽底部形状的曲折性，使得流体流动时的方向转折比平底搅拌槽中的要剧烈，产生的速度波动大。所以锥盘底搅拌槽的固相速度分布更有利于固液两相间的混合。