某CT/1250型缝焊机焊接小车的优化设计
2018-08-28王克用李培超
王 洋,王克用,李培超,张 旭
1 引言
CT/1250型缝焊机是一种为普通碳素带钢连续表面处理生产线卷板接头工序而设计的专用焊机,焊接母材的最大宽度为1250mm。目前国内外钢厂连续表面处理生产线卷板接头工序大多采用该型设备或相近设备。焊接小车是焊机的重要组成部分,焊接及碾压组件、剪切及冲孔组件、焊接变压器及汇流排组件等重要组件均安装在此小车上。因此,焊接小车的制造精度及其整体刚度和强度将影响设备的正常工作,特别是在焊接碾压及剪切冲孔工况,从而直接决定着焊缝的质量。焊接小车上部悬臂梁的组合变形对焊接工序的影响,如图1所示。θ和X分别为梁在焊接力中心所在截面的转角和最大变形位移,Xx分别为X在x、y方向的分量。X在垂直XY平面方向上的分量很小,可忽略不计。由于焊接力及碾压力的共同作用,焊接轮及碾压轮将偏离理论的焊接碾压中心。在焊接过程中特别是在焊接钢板厚度小于0.5mm时,焊接轮将产生滑移导致焊缝撕裂,同时梁的变形也将影响焊接碾压导柱导套的导向精度。上述两点是造成实际焊缝两端质量变差的主要原因。梁的变形对碾压轮的影响与焊接轮类似,这里不再赘述。采用拓扑优化及参数优化的方法对C型小车的结构及参数进行改进设计,提高小车的刚度并减小其质量。

图1 焊接小车上部梁的组合变形对焊接工序的影响Fig.1 Influence of Combined Deformation of the Upper Beam of Welding Tractor on the Welding Procedure
2 C型焊接小车有限元分析
C型焊接小车主要由两侧板、下侧板和其他肋板焊接而成,材料为Q235-B,弹性模量E=210GPa,泊松比μ=0.274,密度ρ=7830kg/m3。建立焊接小车的三维有限元模型,采用修正二次四面体单元进行网格划分,对应力梯度较大的部位加密网格,而对其他次要部位采用较稀疏网格[1]。
在工程实际中,C型焊接小车主要有剪切与冲孔、焊接与碾压两种工况,如图2所示。其中F1=129.382kN,F2=F3=64.691kN,F4=F5=36.796kN,M=15.185kN·m,M1=0.637kN·m。经过有限元分析,得到焊接与碾压工况下的最大位移为1.775mm,发生在上部悬臂梁的远端,即靠近碾压轮及焊接轮的安装位置;剪切与冲孔工况下的最大形变位移为0.167mm,发生在剪切及冲孔油缸的安装位置。由约束条件可知,剪切与冲孔工况下,上部悬臂梁为简支梁,相应的变形较小。进一步分析可知,小车整体结构满足强度要求。下文将主要针对焊接与碾压工况进行研究。

图2 C型焊接小车的两种工况Fig.2 Two Kinds of Working Conditions for the C-type Welding Tractor
3 C型焊接小车拓扑优化
拓扑优化是一种数学方法,目的在于以最少的材料获得结构的最佳性能[2-3],其研究是从最具代表性的Michell桁架理论[4]开始的。随着有限元分析技术的发展,拓扑优化设计在汽车工业领域的应用逐渐开展[5]。文献[6]基于拓扑优化的厢体骨架结构设计,对翼开式厢车进行了轻量化设计。文献[7]基于ANSYS软件,综合拓扑及尺寸优化技术,实现了车架的优化设计。采用基于ANSYS变密度法的拓扑优化方法,以介于(0~1)之间的伪密度ρi为设计变量,以柔度c(ρ)最小化为目标,则相应的拓扑优化数学模型[8]可写成:

式中:K—整体刚度矩阵;U—整体位移列阵;F—整体载荷列阵;p—惩罚因子;v(ρ)—优化域体积,ρ= {ρ1,ρ2,…,ρi}T;vi—第i个单元的体积;v0—模型的初始体积;f—优化域体积分数;n—优化域划分的单元数。
设定优化目标为结构减重30%,选取原模型整体区域为优化区域,对模型进行拓扑优化。拓扑优化过程中有时会出现单元交错排列的网格结构,导致可制造性差,但通过控制最小单元尺寸,可在一定程度上减弱数值不稳定性,进而提高结构的可加工性。优化结果,如图3所示。图3中暗红色区域表示可去除的材料。
结合实际生产装配情况,并根据拓扑优化与有限元分析结果,对原模型进行相应改进,如图4所示。图中编号1、2、…、8表示结构改进的部位,具体内容如下:(1)由变截面改为图示形状,并将高度尺寸增加30mm,从而提高抗弯截面系数。(2)上部增加横向肋板。(3)根据拓扑分析,将倒角增大至C350,共4处。(4)将两侧板改为分段制造,上下两部分分开下料、拼焊制造。这样不但解决了因整体尺寸过大导致下料加工较困难的问题,而且上下两侧板厚度尺寸分开有利于优化及轻量化设计。(5)依据有限元分析结果,将圆角过渡改为斜拉肋板形式以提高刚度。(6)此处开工艺孔,前后共2处,便于变压器及硅整流安装其内。(7)此处增加倒角过渡以减小应力集中。(8)此处后部的肋板厚度由20mm增加至25mm。
在实际设计过程中,拓扑优化往往是在概念设计阶段或结构设计阶段,而产品的设计往往是结构与参数设计并重,下文将对拓扑优化模型进行参数优化。

图3 拓扑优化结果Fig.3 Results of the Topology Optimization
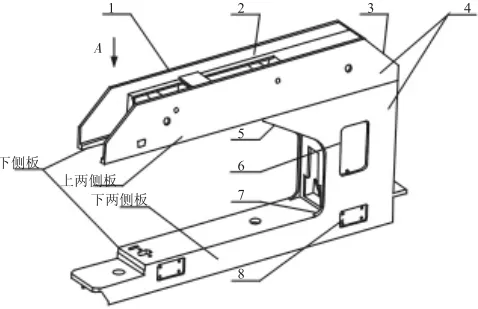
图4 拓扑优化后的改进模型Fig.4 Improved Model After the Topology Optimization
4 C型焊接小车参数优化
4.1 参数的敏感性分析
根据经验,悬臂长度对小车的刚度影响较大。由于焊接板宽、剪切冲孔机构尺寸、焊接碾压机构尺寸以及其他工艺尺寸的限定,1250型设备悬臂长度可变动的范围极小,故不将其作为研究对象。仅研究上两侧板厚度H1、下两侧板厚度H2和下侧板厚度H3三个参数对目标(即模型质量、最大形变位移、最大等效应力、应变能)的影响。
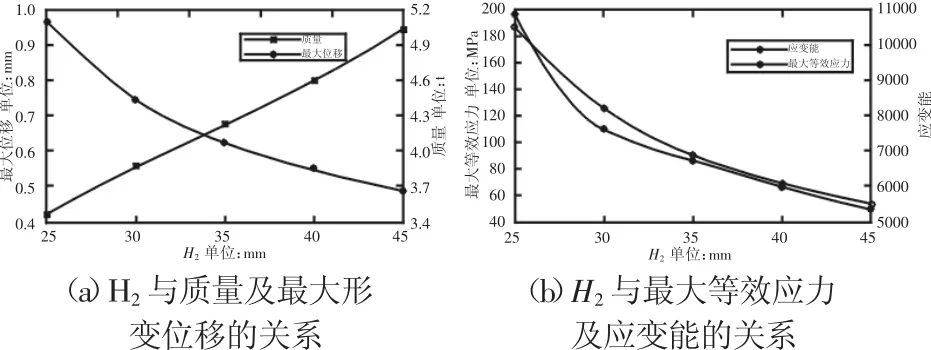
图5 H2的敏感性分析Fig.5 Sensitivity Analysis of H2
为了得到理想的参数优化结果,首先进行结构参数对优化目标的敏感性性分析,进而确定合理的设计变量。下两侧板厚度H2与模型质量、最大等效应力、最大形变位移与应变能的关系曲线,如图5所示。由图5可以看出,随着H2的增大,模型质量逐渐增大,而最大等效应力、最大形变位移及应变能逐渐减小。同时发现,H1、H2、H3均对质量、最大等效应力、最大形变位移以及应变能较为敏感,这说明三个变量均可作为优化设计变量。
4.2 参数优化设计
参数优化设计主要用于产品详细设计阶段,要求在满足约束条件前提下建立参数化模型,运用优化算法获得目标函数的极值,从而得到最优参数[9]。采用序列二次规划算法对参数进行优化,以模型质量最小为目标,以模型最大形变位移vmax≤1为约束条件的数学优化模型[10]为:
式中:f(H)—模型质量;vmax—最大形变位移;H=(H1,H2,H3),Hi—优化变量。在每个迭代点H(k)构造优化模型的一个二次规划子问题,以这个子问题的解作为迭代的搜索方向d(k)进行一维搜索,即:H(k+1)=H(k)+a(k)d(k)
式中:a—步长。原优化模型在迭代点H(k)对应的二次规划子问题QP(d)为:
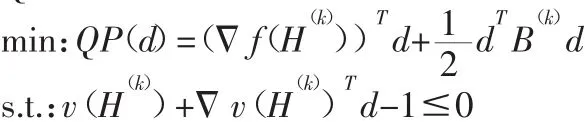
式中:QP(d)—二次规划子问题目标函数;d—搜索方向列阵;Δf(H(k))—在迭代点 H(k)质量矢量对 H(k)一阶偏导;H={H1, H2,H3}Tv(H(k))—在迭代点 H(k)位移矢量对 H(k)一阶偏导数;B—变尺度矩阵;v(x)—形变位移。
以模型质量最小为目标,以模型最大形变位移vmax<1mm为约束条件,优化初始取值为设计变量原始值,允许迭代次数为3000次,收敛容差为ε<0.01。实际计算时,迭代20次后目标收敛。考虑到生产制造实际情况,即上下两侧板尺寸较大且两侧面为无需机加工的非安装面,因此按相近规格的钢板厚度取值。另一方面,下侧板面为剪切、焊接、碾压等安装面且需要精加工,结合敏感性曲线可按优化值取值。优化结果,如表1所示。
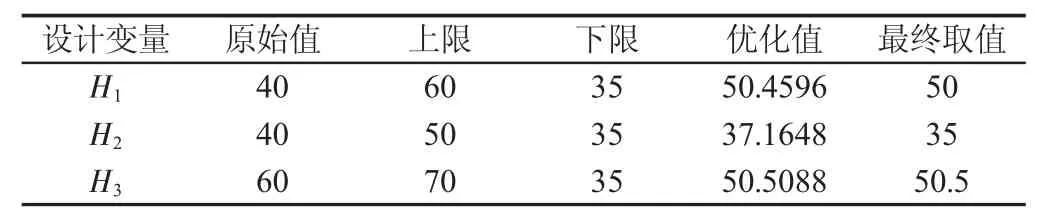
表1 参数优化结果(单位:mm)Tab.1 Results of the Parametric Optimization(Units:mm)
4.3 结果分析及对比
根据参数优化结果,上部两侧板厚度增加意味着上部横梁抗弯截面系数增大而下部两侧板厚减小,这与有限元分析得到的位移及应力云图相吻合。在碾压与焊接工况下,上述改进模型的静力学分析结果表明,最大形变位移为0.85mm,最大等效应力为40.63MPa,模型质量为3.675t。原模型与改进模型位移云图的对比情况,如图6所示。由图可知,优化后的模型质量、最大形变位移、最大等效应力均明显下降。优化前后数据对比结果,如表2所示。
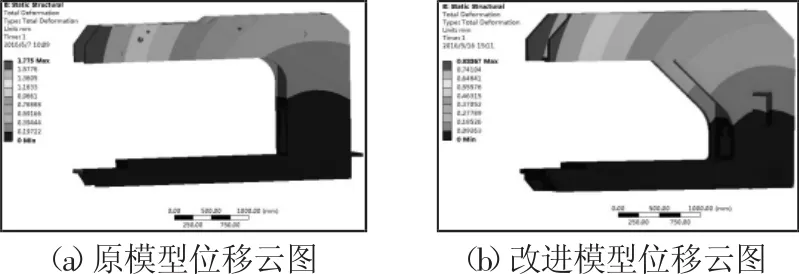
图6 焊接与碾压工况下有限元分析结果对比Fig.6 Comparison of Finite Element Results Under Welding and Rolling Conditions
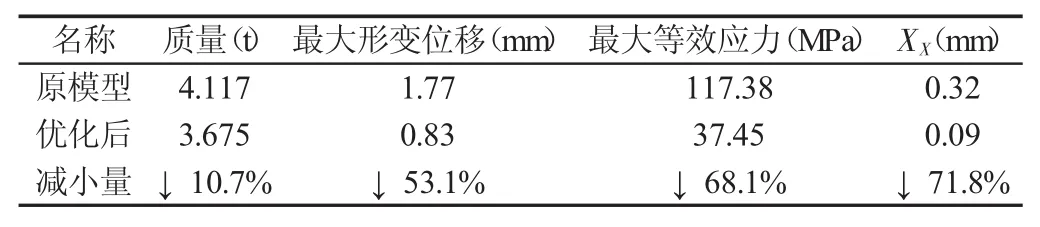
表2 优化前后结果对比Tab.2 Comparison of the Results Before and After Optimization
5 结语
以某1250型缝焊机C型焊机小车为研究对象,首先建立焊接小车三维有限元模型,对小车进行静力学分析。然后以静力学分析结果为基础,在满足整体强度和刚度的前提下,对焊接小车结构进行拓扑优化。最后以质量最小为目标对改进模型进行参数优化设计,获得最终设计值。优化结果表明,模型质量、最大形变位移、最大等效应力、焊接轮在X方向形变位移分别下降了10.7%、53.1%、68.1%和71.8%。通过上述优化设计,小车质量有所减少,降低了制造成本,同时小车的刚度得到明显提高,改善了焊接质量。这里方法为CT/1250型焊机或类似设备的改进设计提供了有价值的参考。
