自消除间隙机构中保护轴承配合过盈量分析

俞成涛，宋 威，刘 聪 ，朱益利

1 引言

相比于传统的保护轴承[1-3]，自消除间隙保护轴承[4-5]由于能够在磁悬浮转子跌落后立即消除滚动轴承外圈与保护轴承系统中支座之间的间隙，从而延长了保护轴承的寿命，提高了磁悬浮轴承的可靠性。文献[4-5]给出了自消除间隙保护轴承的结构、工作原理；对机构的进行了运动学和静力学分析；建立了转子跌落至自消除间隙保护轴承的动力学模型，并对转子跌落后的碰撞力大小进行深入的研究。然而相关研究并没有考虑滚动轴承运行的实际工况。在滚动轴承正常应用场合，其内圈与转子之间需要采用过盈配合方式安装。一方面是防止高速转动时转子与内圈之间发生蠕变；另一方面滚动轴承在出厂时都会存在一定量的游隙，在某些高精度应用场合，也需要消除滚动轴承游隙对旋转精度的影响[6-7]。然而，将滚动轴承应用于自消除间隙机构作为磁悬浮轴承的保护轴承时，整个滚动轴承包括外圈也都以相同的速度随着转子一起高速转动[4-5]。对于这种情况下，除了需要考虑高速旋转产生的离心力对转子与内圈产生的应力与变形，还需考虑离心力对外圈作用产生的变形对轴承游隙的影响；由于游隙的存在会使得外圈在高速旋转时在径向相对于内圈可能产生位移和振动，所以在计算轴承内圈与转子之间的过盈量的时候，除了要考虑内圈与转子之间不会产生蠕变外，还需考虑能在正常的工作转速时将滚动轴承的游隙消除。

为了提高自消除间隙机构中滚动轴承的可靠性，结合自消除间隙机构中滚动轴承的运动特点，对转子与滚动轴承内圈配合过盈量进行了研究，通过建立转子与内圈之间过盈配合的静态和高速旋转时的动态力学模型，详细分析了转子、滚动轴承内圈以及外圈各处的位移。对比分析了两组不同游隙值的滚动轴承在不同转速下所需过盈配合量的大小并进行了强度校核。

2 力学模型的建立

在建立转子与滚动轴承内圈过盈配合力学模型时若忽略端部效应，则过盈配合处内圈的静态和动态求解可分别简化为力学上的厚壁圆筒及等速旋转圆盘问题[7]。由于轴对称性，分析时采用极坐标（r，θ）；此外，无论是装配压力还是离心力，也都是轴对称的，故径向应力σr、切向应力σθ及径向位移u都仅是半径r的函数，即σr（r）、σθ（r）与u（r），而剪切应力τr，θ=0。

2.1 过盈装配的静态力学模型

转子与轴承内圈过盈的配合方式会使转子和内圈由于装配而产生应力，即装配应力。为了对转子以及内圈的静态强度进行校核，建立轴承内圈与转子过盈配合处的力学模型，如图1所示。

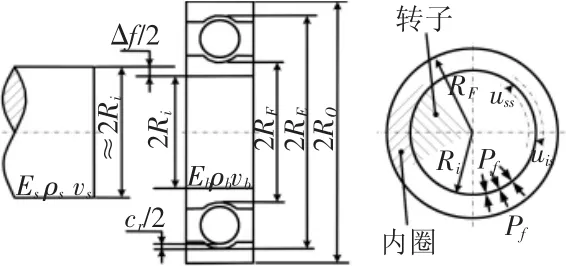
图1 转子与内圈过盈装配的静态力学模型Fig.1 Static Mechanical Model of Interference Fit Between the Rotor and the Inner Ring

图中：Ri—轴承内圈的内圆半径；RF—轴承内圈的当量沟道半径；RE—外圈的当量沟道半径；Ro—外圈的外圆半径；Δf—轴承与转子之间的装配过盈量；cr—轴承的初始游隙；转子与内圈配合面处产生的装配压力为Pf；E、ν、ρ—材料的弹性模量、泊松比和密度；下标s—转子；下标b—轴承。

在极坐标下，分别列写平衡方程、几何方程及物理方程[7-8]：

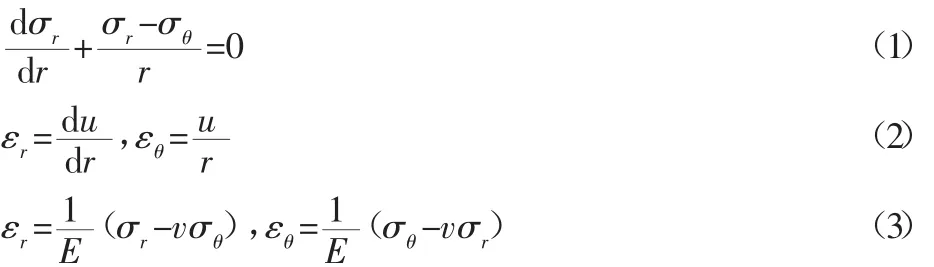
式中：εr、εθ—径向应变与切向应变。

对于轴承内圈，假设其当量沟道处表面不受应力，内圆表面过盈安装于转子上，承受均匀压力Pf，如图1所示。对式（1）～式（3）求解，结合边界条件，可以分别得到轴承内圈静态时的应力、位移分量分别为：

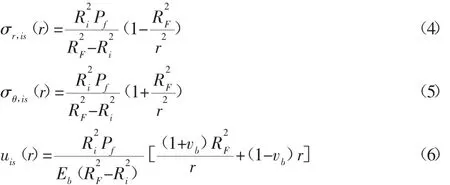
静态时滚动轴承的外圈并不受到转子与内圈之间过盈配合的影响，故滚动轴承外圈静态应力和位移都为零。

转子与内圈之间的装配过盈量与转子和内圈的径向位移之间有以下关系：

将式（6）和式（8）代入上式，可以得到转子与内圈之间的静态装配压力Pf为：

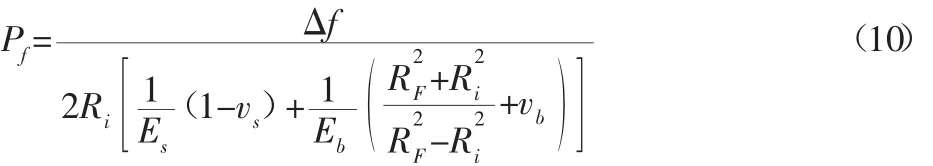
2.2 高速旋转时的动态力学模型

转子高速旋转时，由于离心力的缘故，转子与轴承内圈各处会产生相应的应力和位移，同时在这里的方案中，由于外圈也是随着转子一起转动，所以外圈也会在离心力作用下产生相应的应力和位移。转子和滚动轴承在离心力作用的变形，如图2所示。

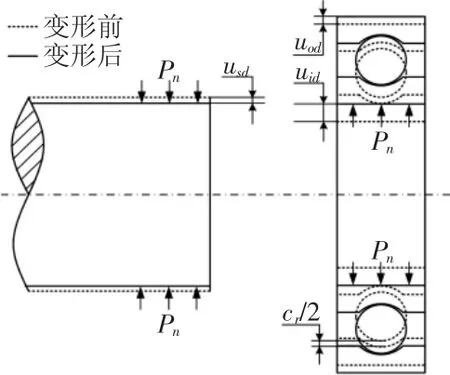
图2 高速旋转时转子与轴承的变形Fig.2 Deformation of the Rotor and the Ball Bearing at High Speed Rotation

设转子的旋转角速度为ω，材料的密度为ρ，此时的基本方程为[7-8]：

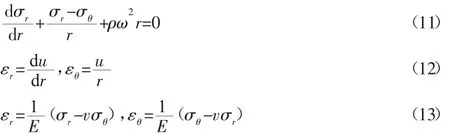
转子与内圈高速旋转受到离心力作用后，转子与内圈之间的初始装配过盈量会由于转子外圆表面与内圈内圆表面产生不同的位移大小而发生变化，导致转子与内圈之间的配合压力随之发生变化。设转子与内圈之间动态配合压力为Pn，如图2所示。与静态力学模型同理，求解得到此时转子的应力、位移分量分别为：

得到内圈的动态应力、位移分量分别为：

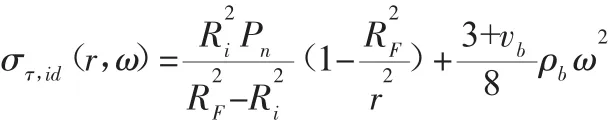
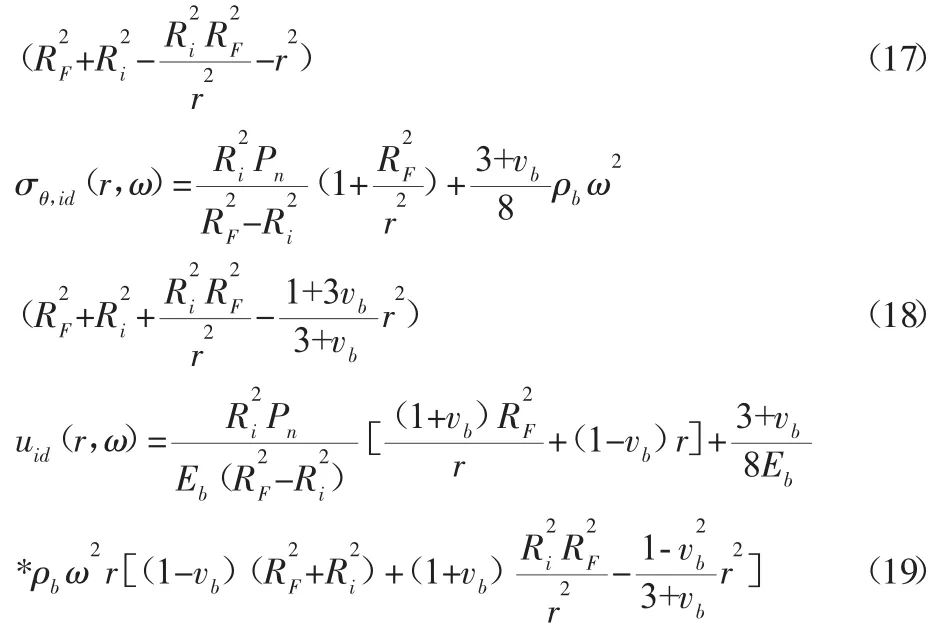
对式（14）～式（19）分析可以看出，转子和内圈产生的动态应力和位移都包含Pn项和ω项。其中Pn项为装配产生，而ω项为离心力产生。由于外圈不受过盈配合力的作用，把内圈中含有Pn项去掉，并用外圈的结构参数替换，即得到外圈产生的动态应力和位移量分别为：

滚动轴承内、外圈当量沟底半径可以根据轴承的内、外径计算得到：

其中，ηi，ηo的实用值可查表得到。

3 转子计算结果分析

这里所用转子和滚动轴承的结构及材料参数，如表1、表2所示。对式（16）、式（19）和式（22）中的离心力项计算，可以分别得到转子外圆表面、内圈内圆表面、内圈沟道处以及外圈沟道处的位移随转速的关系，如图3所示。从图3可以看出，同一转速下，外圈沟道处位移＞内圈内表面位移＞内圈沟道处位移＞转子外表面位移；随着转速的增加，转子外表面、内圈内表面和内圈沟道处的位移增加较为缓慢，而外圈沟道处的位移增加较为迅速，并且转速越大，其增加的速度越快；通过对比可以发现内、外圈沟道位移差明显大于转子、内圈配合面位移差，并且转速越高越明显。图3的结果说明，离心力作用下内、外圈的变形位移使得轴承的游隙增加，并且转速越高，轴承的游隙增加的越大。所以在实际应用时，为了保证滚动轴承中的滚珠和外圈随内圈一同旋转时的稳定性，需要通过转子与内圈之间的过盈装配消除轴承高速转动时的游隙。

表1 转子的材料参数Tab.1 Material Parameters of the Rotor

表2 滚动轴承的结构及材料参数Tab.2 Structural and Material Parameters of the Ball Bearing

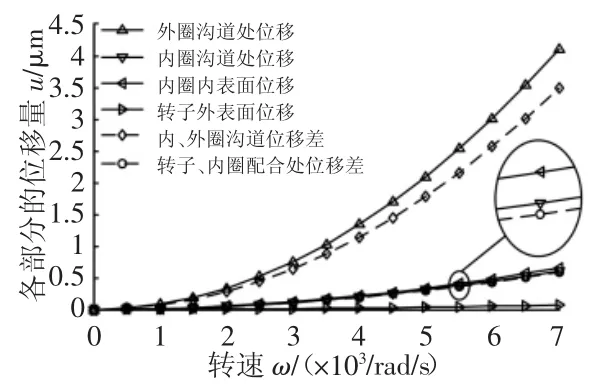
图3 各部分由于离心力作用的位移量与转速的关系Fig.3 Relationship Between the Displacement of Each Part and the Rotational Speed Due to Centrifugal Force

根据式（19）和式（22）可以得到不同转速下轴承的内部游隙为：

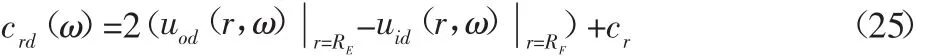
根据图2的变形几何关系，轴承内、外圈的位移需要满足：

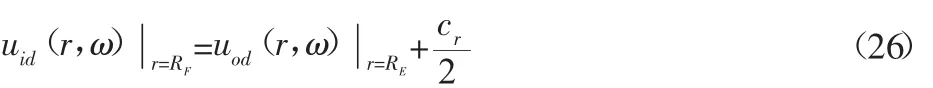
将式（19）和式（22）代入上式可以得到在不同的工作转速下动态配合压力Pn，再将得到的Pn代入式（16）和式（19）得到转子与内圈分别在接触面处的位移量；根据其位移量就可以得到各个转速下转子与轴承内圈之间所需的装配过盈量为：

对上式分析可以得到Δf（ω）实际上包含三个部分，即：

式中：Δf1—消除离心力对内、外圈沟道产生的位移量所需的装配过盈量；Δf2—消除轴承初始游隙所需的装配过盈量；Δf3—抵消转子、内圈的配合面处在离心力作用下的位移所需的装配过盈量。

图4 转子与内圈装配过盈量计算流程图Fig.4 Flow Diagram of Calculation of Interference Fit Between the Rotor and Inner Ring

根据转子与内圈位移量得到装配过盈量Δf后，还需要对Δf分别进行转子、内圈和外圈的动、静态强度验证。转子与内圈装配过盈量计算流程图，如图4所示。

针对这里的滚动轴承，选取了两组游隙值进行分析：C2组，游隙值为（0～9）μm和C0组（标准组），游隙值为（3～18）μm。分别取其平均值进行计算，即C2组取4.5μm；C0组取10.5μm。根据式（27）得到装配过盈量Δf与转速的关系，如图5所示。

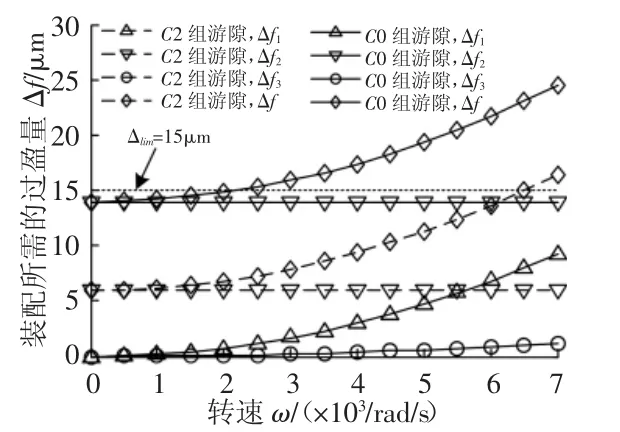
图5 转子与内圈所需的装配过盈量与转速的关系Fig.5 Relationship Between the Interference Fit Between the Rotor and the Inner and Rotational Speed

从图5中可以看出，相对于轴承游隙和内、外圈沟道位移，内圈与转子变形所需的装配过盈量（Δf3）很小；消除内、外圈沟道位移所需的装配过盈量（Δf1）只与转速有关，并随着转速的增加而增加，在转速为7000rad/s时达到9.3μm；而消除轴承初始游隙所需的装配过盈量（Δf2）经计算约为轴承游隙的1.33倍，并且不同组游隙对Δf3和Δf1无影响，只是相应的Δf2项增加或减小1.33倍的游隙增加或减小值。图5表明转子与内圈之间装配过盈量主要用于消除轴承初始游隙以及高速旋转时内、外圈沟道处位移产生的游隙增加量，并且轴承初始游隙和转速的增加都会使得转子与内圈的装配过盈量显著增加。

考虑到装配工艺，对于大过盈量的滚动轴承，常用的装配方法是热套装配法，将轴承放入矿物油中加热，一般加热温度在（80～100）℃，为了防止发生回火效应，滚动轴承的加热温度不能超过120℃。轴承内圈受热膨胀量可由下式计算得到：

式中：a—轴承受热线膨胀系数，大约为12.6×10-6（1/℃）。

以加热最高温度120℃，环境温度20℃计算，热套装配的最大过盈量为：Δlim=12×100×12.5×10-6=15μm （30）

从图5可以看出，若选择C0组游隙的滚动轴承，其仅仅用于消除轴承初始游隙所需的装配过盈量就已经达到14μm，基本达到热套装配的最大过盈量了；而选择C2组游隙的滚动轴承，在转速为6500rad/s时达到热套装配的最大过盈量。所以，为了方便滚动轴承的正常装配，应该选择小游隙（C2组）的滚动轴承，并且当工作转速所需的装配过盈量大于热套装配最大过盈量时，在转子与内圈装配过程中可能需要采取热套和其他方式共同装配方式。

当采用C2组游隙的滚动轴承时，转子、轴承内圈和外圈径向各处在各个转速下的应力情况，如图6～图8所示。

图6 不同转速下转子的动态应力情况Fig.6 Dynamic Stress of the Rotor with Different Rotational Speeds

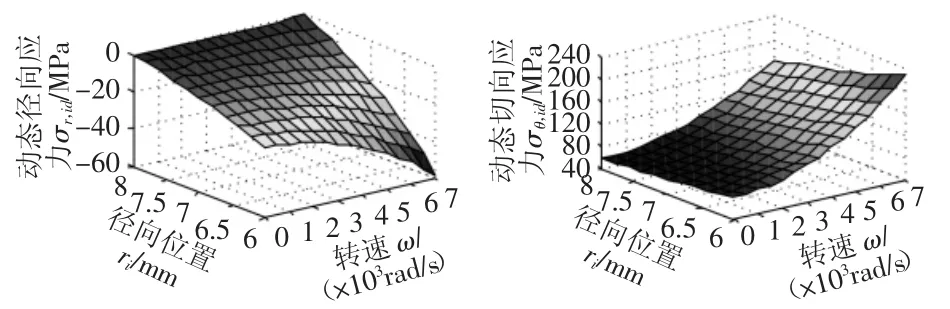
图7 不同转速下内圈的动态应力情况Fig.7 Dynamic Stress of the Inner Ring Under Different Rotational Speeds

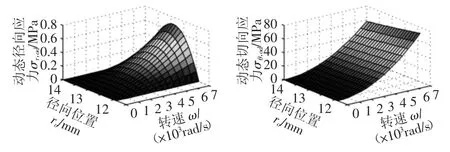
图8 不同转速下外圈的动态应力情况Fig.8 Dynamic Stress of the Outer Ring Under Different Rotational Speeds

从图6可以看出，转子径向各处受到的径向、切向应力均为压应力且数值上基本相等，切向应力数值上略小于径向应力，径向、切向压应力均随着转速的增加而增大，从轴心到外圆逐渐增大。图7表明内圈径向各处受到的径向应力为压应力，数值上随着转速的增加而增大，同一转速下，最大径向应力出现在内圈内表面处；而其受到的切向应力为拉应力，随着转速的增加而增大，同一转速下，从内表面到外沟道处的切向应力逐渐减小。从图8可以看出，各个转速下，外圈受到的最大径向应力出现在中间部位，最大径向应力随着转速的增加而增大，外圈的内沟道以及外圆表面处的径向应力均为零，且不随着转速的变化而变化；而外圈径向各处的切向应力随着转速的增加而增加，且同一转速下，从内沟道处到外圆表面的切向应力逐渐减小。对图6，图7和图8各个应力数值上对比可以发现，各个转速下以内圈内表面处受到的切向应力为最大，其次为外圈受到的切向应力。这是因为过盈装配和离心力作用均对内圈产生切向拉应力效果，而外圈则是由于较大的半径使得高速下离心力作用产生较大的切向应力。

4 静态强度验证

图9 静态装配压力随转速的变化关系Fig.9 Relationship Between the Static Fit Pressure and Rotational Speed

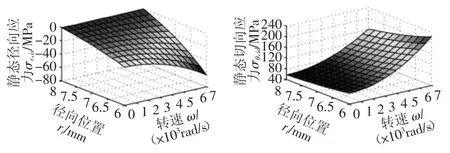
图10 内圈的静态应力分布情况Fig.10 Static Stress Distribution of Inner Ring

对转子和内圈进行静态强度验证，由式（7）可以得到，转子径向各处的径向和切向应力与位置无关，故其静态的径向和切向应力相等都为-Pf，且只与转速相关，Pf与转速的关系，如图9所示。而内圈的静态应力分布情况，如图10所示。

将图9与图6对比可以发现，转子静态时受到的压应力略大于转子转动后受到的动态压应力，这是因为转子转动后转子与内圈配合面处的径向位移使得其之间的过盈量略微减小，从而导致转子受到的动态应力略为减小。将图10和图7对比发现，内圈径向各处受到的静态径向压应力和切向拉应力在数值上也都略大于转子转动后内圈受到的应力大小，也是受到其配合面处的过盈量在转动后略微减小的影响。

考虑到磁悬浮轴承失效后自消除间隙保护轴承中滚动轴承工作时，其外圈的转速减小为零，此时外圈由于离心力作用发生的变形量也减小为零。则图5中用于消除内、外圈沟道位移所需的装配过盈量Δf1，会导致滚动轴承处于负间隙的状态下工作。从图3中可以得到当转速为3140rad/s（500Hz）时，滚珠与内、外圈之间的预紧量约为0.6μm；但是当转子转速达到7000rad/s时，滚珠与内、外圈之间的预紧量则达到了3.5μm。少量的预紧有利于增加滚动轴承的刚度、承载力以及平稳运行[6]，但预紧量过大可能会导致滚珠与内、外圈之间的阻力增大并加速滚动轴承的磨损甚至卡死。

5 结论

（1）磁悬浮轴承转子正常运行时，自消除间隙机构中的滚动轴承的内部游隙随着转速的增加而增大。（2）在选取自消除间隙机构中的滚动轴承时，应该尽量选择小游隙的滚动轴承，并且需要结合磁轴承转子的工作转速计算出滚动轴承安装所需的过盈量，从而选取合适的装配方式。（3）当自消除间隙机构工作时，滚珠与内、外圈之间的间隙为小于零，并且磁悬浮转子的转速越高，其数值越大，可能会导致滚动轴承失效。