基于四通道卷积稀疏编码的图像超分辨率重建方法

陈 晨，赵建伟，曹飞龙

(中国计量大学信息与数学系，杭州310018)(*通信作者电子邮箱zhaojw@amss.ac.cn)

0 引言

图像超分辨率重建是将给定的低分辨率图像恢复成高分辨率图像的一种图像处理技术。因为图像超分辨率重建过程是一个病态问题，所以不同的重建方法可以恢复出不同的高分辨图像，但这些重建方法的关键点在于通过先验知识去寻找合适的低分辨率图像与相应的高分辨率图像之间的内在联系。

近年来，国内外学者提出了许多基于样本的超分辨率图像重建方法［1－8］。这些方法主要通过低分辨率和其相应的高分辨率补丁对来学习低分辨率和高分辨率图像之间的映射关系，或者寻找相同图片的内部相关性。Yang等［6］利用压缩感知的思想［9－10］，提出了基于稀疏表示理论的超分辨率图像重建方法。该方法假设低分辨率图像补丁在低分辨率字典下的稀疏表示系数与其对应的高分辨率图像补丁在高分辨率字典下的稀疏表示系数是相同的，因此，高分辨率图像补丁就可以通过训练好的高分辨率字典和求得的低分辨率图像补丁的稀疏表示系数获得。在文献［6］的基础上，Yang等［7］通过整幅图像重叠补丁的分解和紧凑字典对的训练来降低算法的复杂度，该方法称为稀疏编码超分辨率重建(Sparse Coding Super-Resolution，SCSR)。尽管SCSR算法在超分辨率图像中取得了很好的重建效果，但是将整幅图像分解为重叠的补丁过程会破坏图像整体的一致性。考虑到这个问题，Zeiler等［11］提出了卷积稀疏编码模型。该模型不再将图片拆分成为重叠补丁，而是将整幅图片作为输入进行重建。输入的低分辨率图像Y可以表示为r个滤波fi和相对应的特征图Zi的卷积和:

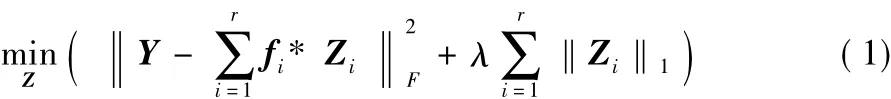
其中:Y表示输入尺寸为m×n的图像;fi表示大小为s×s的第i个滤波;Zi是相应大小为(m+s－1)×(n+s－1)的特征图。该模型有效地避免了将图片拆分成重叠的补丁来进行重建所带来的不足。Gu等［12］将模型式(1)应用到图像超分辨率重建中，得到名为卷积稀疏编码(Convolutional Sparse Coding，CSC)的超分辨率重建方法。

在图像分类中，为了提高分类的精度，人们通常将输入图像通过变换生成一组相关图像，再将该组图像的平均值作为输入进行分类，这里最常见的变换有剪裁与翻转［13］。由于文献［12］中的基于卷积稀疏编码的超分辨率重建方法着重于恢复图像的高频细节部分，高频细节部分通常是人们视觉关注的部分，它们更能直观地反映图像的清晰度;因此，本文在卷积稀疏编码的基础上，将图像的翻转思想用于图像超分辨率重建，即将图像依次进行 90°、180°、270°和 360°翻转作为输入，建立四通道的卷积稀疏编码的超分辨率图像重建方法，以增强图像的轮廓细节特征，增加算法的稳定性。

1 四通道卷积稀疏编码超分辨率重建

本章将阐述四通道卷积稀疏编码超分辨率重建方法。该算法将图像依次翻转90°、180°、270°和360°后作为每一通道的输入。在每一通道，先将输入的低分辨率图像分解为低频和高频两部分［12］，然后分别用卷积稀疏编码算法和三次插值方法对低分辨率图像的高频部分和低频部分进行重建，最后加权求均值获得重建的高分辨率图像。算法的具体流程见图1所示。以下将对每一通道的超分辨率图像重建进行阐述。

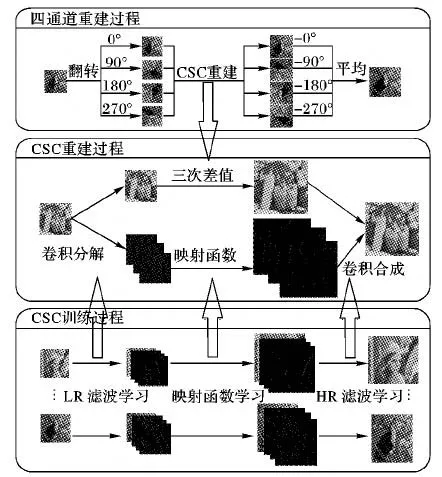
图1 四通道卷积稀疏编码超分辨率重建方法流程Fig.1 Flow chart of four-channel convolutional sparse coding based super-resolution reconstruction method

1.1 低分辨率图像的高频与低频部分分解

为了能够更好地将低分辨图像的纹理和细节信息进行超分辨率重建，本节先将要重建的低分辨率图像Y分为低频部分Yl和高频部分Yh，即Y=Yl+Yh。

为了获得低分辨率图的低频部分Yl，首先利用式(2)来提取低频特征图:

其中:ZY是低分辨率图像Y的低频特征图;fp是大小为3×3的元素全取为1/9的低通滤波;fdh=［－1，1］和fdv=［－1，1］T分别是水平梯度算子和垂直梯度算子。

对于优化问题式(2)，可以通过快速傅里叶变换在傅里叶域中求解得到，即:

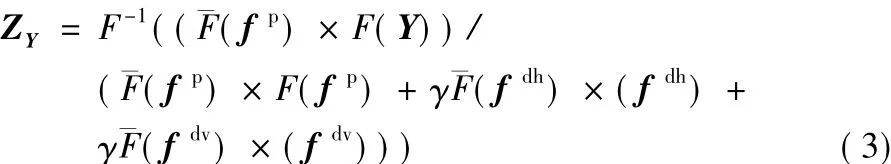
其中:F和F－1分别表示傅里叶变换和傅里叶逆变换;珔F表示傅里叶变换的复共轭。

根据式(3)可以求得低分辨率图Y的低频特征图ZY，由此可以计算得到低分辨率图像Y的低频部分Yl和相应的高频部分Yh:

1.2 低分辨率图像高频部分的超分辨率重建

本节将利用卷积稀疏编码［12］对低分辨率图像的高频部分Yh进行重建。首先利用训练样本得到一组低分辨率滤波，利用这组低分辨率滤波分解高频部分Yh得到低分辨率特征图;其次，利用训练样本建立的低分辨率特征图与高分辨率特征图之间的映射关系来确定高分辨率特征图;最后，根据学习得到的高分辨率滤波和高分辨率特征图重建得到低分辨率图像Y的高频部分Yh的高分辨率图像Xh，具体步骤如下。

1.2.1 基于CSC获取低分辨率特征图

对于给定的训练图片样本对{Pj，Qj)}，其中 Uj是低分辨率图，Vj是相应的高分辨率图。利用下面的卷积稀疏编码模型可以得到低分辨率滤波:1

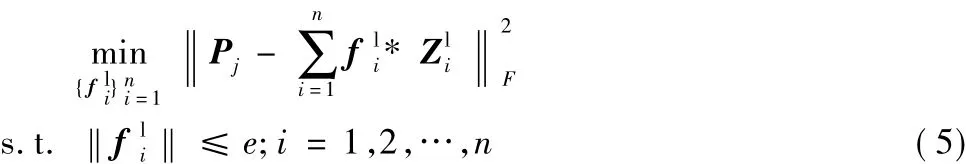
考虑到计算机的内存问题，优化模型式(5)可以通过随机交替方向乘子法(Stochastic Alternating Direction Multiplier Method，SADMM)［14］求解，得到低分辨率滤波。引入增广变量s=fl，拉格朗日变量d，令Zl= ［()T，()T，…，()T］，L为(Zl)TZl特征值的上界，则式(5)的迭代解为:

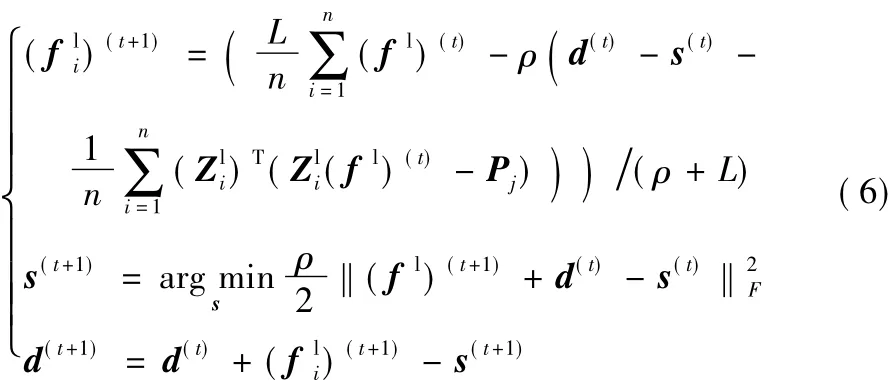
hs.t.≤ 1，i=1，2，…，n

对于优化模型式(7)，可以通过交替方向乘子算法求解得到低分辨率特征图15］。引入辅助变量 Mi=和对偶变量Ui，则式(7)的迭代解为:

这里:

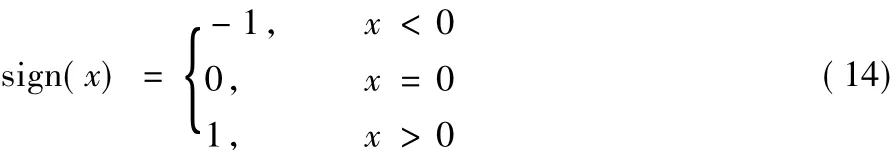
1.2.2 基于CSC获得高分辨率特征图和高分辨率滤波

对于给定的放大倍数k，设高分辨率特征图和低分辨率特征图有如下关系:

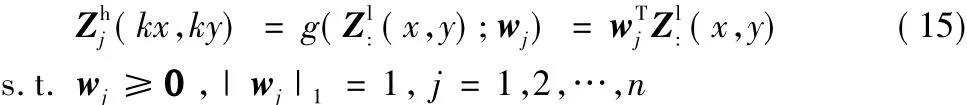
其中e是限制高分辨率滤波的标量。对于优化问题式(16)，也可以通过随机交替方向乘子算法［14］求解。

1.2.3 高频部分和低频部分的高分辨率图

对于低频部分Yl，采用双三次插值进行高分辨率重建，得到相应的高分辨率图Xl。最后，合并高分辨率图Xh和Xl，得到低分辨率图Y的高分辨率图X:

为了加强重建效果，采用后投影法［16－17］对重建好的高分辨率图X进行进一步的处理。

1.3 图像超分辨率重建算法

综合1.1和1.2节的分析，给出四通道卷积稀疏超分辨率重建算法的测试过程，具体算法步骤如下:

步骤2 将低分辨率图像Y分解成低频Yl和高频Yh两部分。

步骤3 对每一通道采用卷积稀疏编码方法重建相应的高分辨率图像的高频部分Xh。

1)通过式(7)求解出高频部分Yh的低分辨率特征图。

2)通过式(15)求解出高频部分Yh的高分辨率特征图。

3)通过式(17)求解出高分辨率图像的高频部分Xh。

步骤4 对每一通道，采用三次插值的方法重建低分辨率图像低频部分Yl的高分辨率图像Xl。

步骤5 将四个通道重建出的高分辨率图像加权求均值输出最终的高分辨率图像X。

2 实验与结果分析

本章中将本文所提的四通道卷积稀疏编码超分辨率重建方法与其他一些超分辨率图像重建方法进行实验比较。

2.1 实验设置

本文中采用文献［6］中的训练集训练低分辨率和高分辨率滤波，即将91张训练图片随机拆成大小为72×72的1000个子块进行训练，这里的低分辨率滤波的尺寸大小为5×5，数量为800个，相应的高分辨率滤波大小为5×k，数量为1200个，其中k为放大倍数。正则化参数γ取30，λ取0.02，对于放大倍数2和3的限制高分辨率滤波的常量e分别取4和9。实验在Intel Xeco CPUE5-2630V3的Matlab R2015b上运行。

本文采用以下两种经典的标准峰值信噪比(Peak Signalto-Noise Ratio，PSNR)和结构相似度(Structural Similarity，SSIM)［18－19］来评价超分辨率重建效果:

其中:

其中:p是图像的行数;q是图像的列数;X是重建的图像;Xori是原始的高分辨率图像。

其中:

其中:α1，α2和α3是权值;xi表示将图像X拉成向量的第i个像素值;μX表示X的亮度估计;σX表示X的对比估计;C1、C2、C3都是常数。在实验中，α1、α2和 α3设置为 1，C1，C2，C3取值为 C1=(K1L)2，C2=(K2L)2，C3=C2/2，其中 L是图像的最大像素值，灰度图像默认值为255，K1K21，取 K1=0.05，K2=0.05。通常情况下，PSNR 值和 SSIM 值越高，表示重建图像的效果越好、结构越准确。

2.2 四通道的优势

本节将本文所提的四通道卷积稀疏编码(Four-Channel based convolutional Sparse Coding，FCSC)和 CSC进行比较。为了保证对比实验的准确性，将采用同样的滤波和映射函数以及相同的正则项参数对测试图像进行恢复。对15幅经典的测试图像进行实验，由于图像的重建结果相似，选取其中的5张测试图像在表1中进行展示。

从表1的实验结果可以看出，采用四通道卷积稀疏编码方法要比单通道上的卷积稀疏编码要重建效果好。

表1 放大因子为2的不同重建方法PSNR对比 dBTab.1 PSNR comparison of different reconstruction methods with magnification factor of 2 dB

2.3 图像超分辨率重建

本节将本文所提方法与一些超分辨率图像重建方法，如固定邻域回归(Anchored Neighborhood Regression，ANR)算法［4］、调整后的固定邻域回归(Adjusted anchored neighborhood regression，A+)算法［5］、SCSR［7］、Zeyde 等［8］提出的基于稀疏表示的单幅图像放大方法(记为Zeyde)、CSC［12］和自适应的稀疏域选择 (Adaptive Sparse Domain Selection，ASDS)方法［20］进行比较。选取常用的15张图像作为测试图像，其相应的PSNR和SSIM值如表2～3所示，其扩大因子分别为2和3。

从表2和表3中可以看出，本文所提的方法在扩大因子2和3的情况下图像的重建效果比其他对比方法均有所提高。在扩大因子2的情况下，本文所提方法能取得较高的PSNR和SSIM值。虽然本文方法并不能保证在每幅测试图像上取得最高值，但是在大部分图像上能取得较好的重建效果。同样地，在扩大因子为3的情况下，相对于其他方法，本文所得方法所得的效果比较好。其中2幅图像的重建结果如图2和图3中所示。

2.4 抗噪性实验

实际生活中采集到的图像往往存在噪声干扰，因而算法是否具有一定的抗噪性将会直接影响到重建图像的质量。为了验证本文所提方法的抗噪性能，将对含有少量噪声的图像进行测试。在实验中，先对测试图像分别添加了均值为0.1、方差为0.02的高斯白噪声，其超分辨率重建实验结果如表4所示。

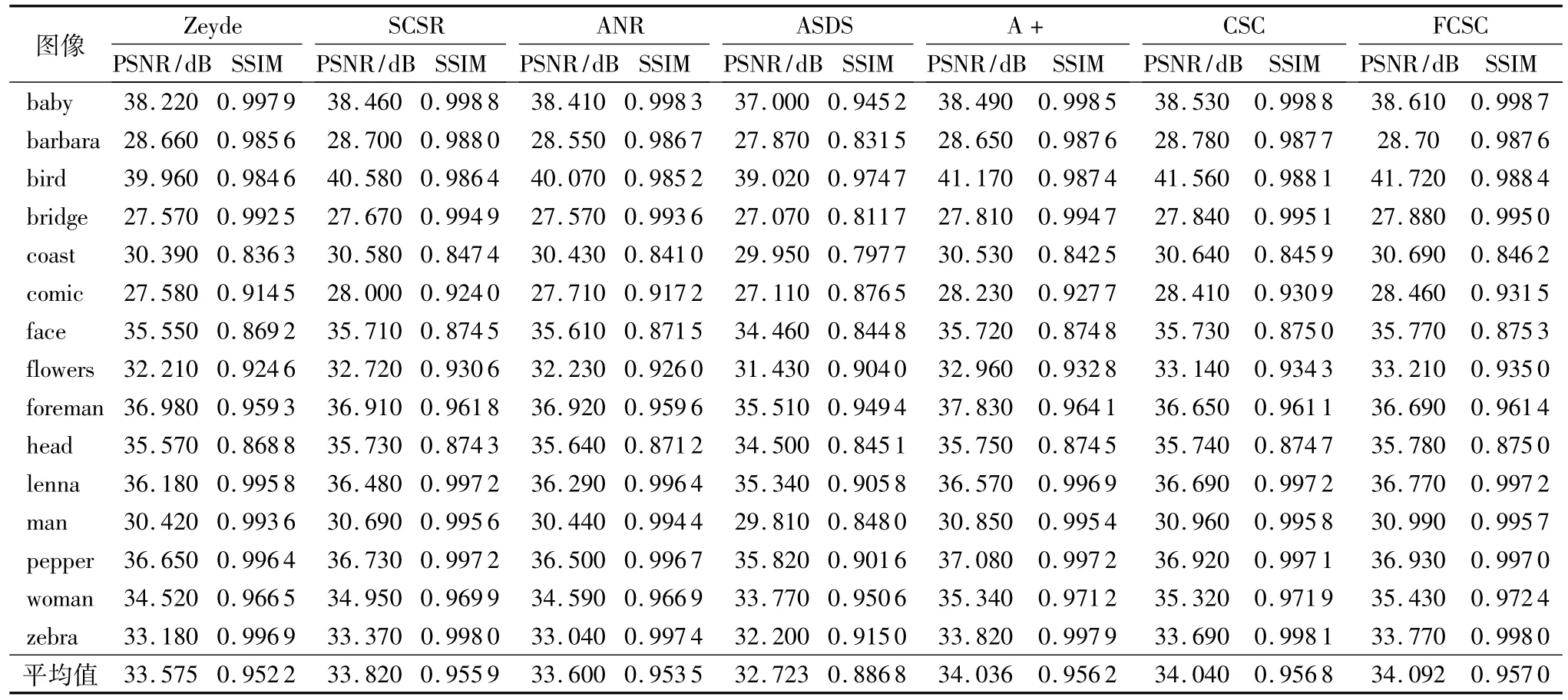
表2 放大因子为2时不同图像重建方法重建性能对比Tab.2 Reconstruction performance comparison of different image reconstruction methods with magnification factor of 2

表3 放大因子为3时不同图像重建方法重建性能对比Tab.3 Reconstruction performance comparison of different image reconstruction methods with magnification factor of 3

图2 放大因子为2时，不同图像重建方法在图像pepper上的重建效果比较Fig.2 Reconstruction effect comparison of different image reconstruction methods on image pepper with magnification factor of 2

图3 放大因子为3时，不同图像重建方法在图像man上的重建效果比较Fig.3 Reconstruction effect comparison of different image reconstruction methods on image man with magnification factor of 3

表4 放大因子为3时不同图像重建方法在高斯噪声下的重建性能对比Tab.4 Reconstruction performance comparison of different image reconstruction methods under Gaussian noise with magnification factor of 3

从表4中可以看出，虽然本文所提方法的SSIM值低于传统的CSC模型，但是比其他重建方法要更稳定。另外，本文所提方法的PSNR值高于传统的CSC模型，表明本文的方法重建的图像在结构上具有更好的相似性。

表5是测试图像添加密度为0.01的椒盐噪声的比较结果。从表5可以看出，本文所提方法在抵抗椒盐噪声的性能上均优于其他超分辨率重建方法。

本文所提的方法采用四通道并行的方式来重建超分辨率图像，因而主要的计算量集中在通过卷积稀疏编码模型求解稀疏特征图上。文献［12］指出，卷积稀疏编码模型每一次迭代求解稀疏特征图的复杂度主要由快速傅里叶变换决定，且复杂度为Ο(KN log N)，其中K为滤波个数，N为输入图像的像素点的个数。

表6是本文所提的超分辨率重建方法FCSC与其他重建方法在bird图像上所用的时间。

从表 6 可以看出，Zeyde［8］、ANR［4］和 A+［5］的方法所用的时间很少，不足 1 s;SCSR［7］需要 56 s，而 CSC［12］和本文所提的方法所用的时间超过1 min，分别为74 s和76 s，主要是在滤波分解求解特征图时花了较多的时间，ASDS［20］则用了最长的时间。

表5 放大因子为3时不同图像重建方法在椒盐噪声下的重建性能对比Tab.5 Reconstruction performance comparison of different image reconstruction methods under pepper＆ salt noise with magnification factor of 3

表6 不同图像重建方法的重建时间对比 sTab.6 Reconstruction time comparison of different image reconstruction methods s

3 结语

本文针对图像分辨率较低的问题，提出了四通道卷积稀疏编码超分辨率重建方法。该方法采用并行的四通道对输入的低分辨率图像的高频部分进行卷积稀疏编码重建，再通过均值化有效地提高模型的稳定性、增强图像的结构相似性，克服重叠补丁对图像一致性破坏的缺陷。实验比较结果表明，本文所提的方法比一些经典的超分辨率重建方法在PSNR、SSIM和抗噪性上具有更好的重建效果。

本文在对低分辨率图像的高频部分进行稀疏卷积编码时，正则化参数选取经验值。下一步将讨论正则化参数对所有图片的自适应性。