一块简支石墨烯片动力响应的小尺度效应研究

谢根全， 王建平， 张琦珑

(1. 湖南科技大学 土木工程学院， 湖南 湘潭 411201； 2. 绵阳职业技术学院， 四川 绵阳 621000)

纳米材料具有高强度和很好的储能性，在化学领域具有很好的催化效果等优点，因而具有很好的应用前景。为了充分利用纳米材料的优良性质，研究这种材料的物理和力学性质显得十分重要。因为纳米材料的小尺度效应和表面效应，如果用经典连续介质力学方法研究纳米材料的力学问题会导出不精确甚至错误的结论。值得庆幸的是Eringen等[1]提出的非局部弹性理论能够克服经典连续介质力学的这一缺陷。 Zhang等[2]应用非局部弹性理论研究了多壁碳纳米管的屈曲问题Xie等[3-5]研究了碳纳米管的小尺度效应和振动特性。Snchez-Portal等[6]基于非局部弹性和高阶剪切理论研究了单层石墨烯片的屈曲。 Zhang等[7]应用杂交非局部梁模型研究了微观/纳米梁的弯曲、屈曲以及振动。 Reddy[8]提出了可用于梁和板的经典弯曲和剪切变形的非局部非线性理论。 Fang等[9]基于非局部理论研究了双壁碳纳米管的非线性振动。Liang等[10]对石墨烯片的非局部小尺度参数进行了预测。最近，Miandoab等[11]应用非局部和应变梯度模型研究了静电驱动的硅纳米梁。

本文将非局部模型引入石墨烯片的动力响应研究中， 研究了石墨烯片动力响应的小尺度效应。

1 理论公式

1.1 非局部应力

在Eringen[12]的非局部弹性理论模型中，Eringen认为弹性体内某点的应力不仅与该点的应变有关而且与弹性体内其它点的应变有关，这是因为纳米材料内的原子或分子之间的长程力相互作用引起的，由非局部理论得到的结论与晶体动力学的原子理论以及声子散射的实验观察一致。非局部弹性体的本构方程最一般的形式是整个影响区域的积分形式。

对于均质各向同性材料, 其本构方程为

(1)

式中： “:”为双点积；C0为经典各向同性连续介质的弹性模量矩阵；σ(x)为在x点非局部应力张量；ε(x′)为弹性体内任意点x′处的应变张量；核函数α(|x′-x|,τ)为非局部模量, |x′-x|为欧几里得距离,τ=e0a/l中的e0为适合所有材料的常数,a为一个内部特征长度(如原子间距离， 晶格空间, 颗粒间距等)，l为一个外部特征长度(如裂纹长度，波长等)。式(1)中的体积积分是对整个弹性体而言的。 但是，虽然文献[10]对“扶手椅”和“锯齿形”石墨烯片的非局部小尺度参数做了预测，而且作者认为小尺寸参数与边界条件有关，没有对螺旋形石墨烯片的小尺寸参数进行预测。为了研究简支石墨烯片的小尺度效应和螺旋角对小尺度效应的影响，基于非局部弹性理论的概念，我们选择石墨烯片的基本六边形单元作为研究对象，如图1所示。

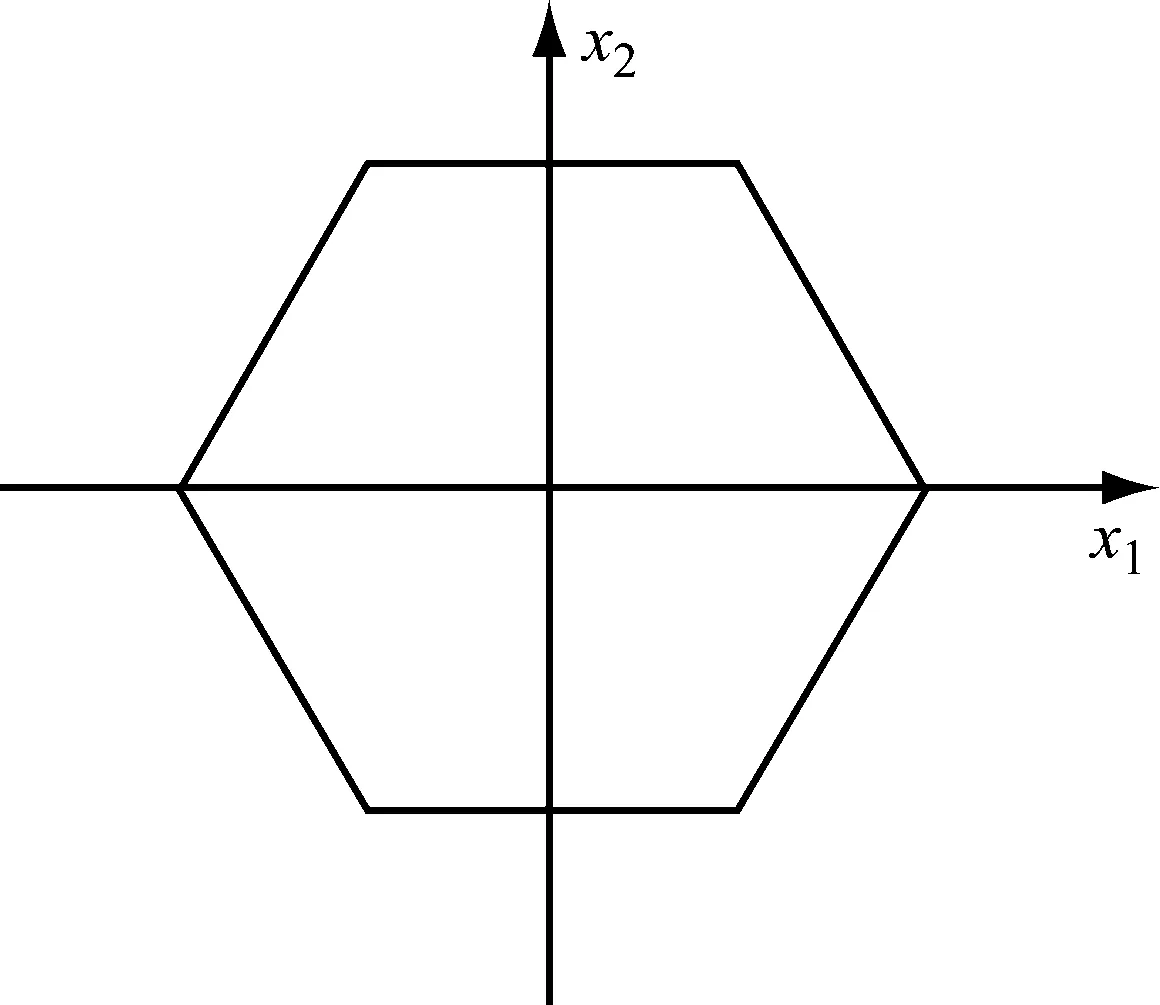
图1 石墨烯片的一个代表单元

六边形代表单元内一点(x1,x2)处的应力分量可以展开成泰勒级数形式

(2)

式(2)两边对六边形代表单元积分，并求平均值，根据单元关于坐标的对称性，并略去2阶以上的高阶项为

(3)

式中：l为C-C键长；〈σij(x1,x2)〉为非局部应力。

对式(3) 求逆有

(4)

2.2 几何方程

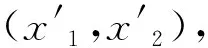
整体坐标系中，石墨烯片的几何方程为

εi′j′=-zw,i′j′

(5)

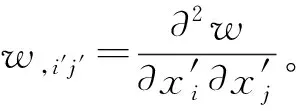
根据应变变换关系，局部坐标系中的应变张量为

εij=lij′εi′j′li′j

(6)

其中,

(7)

εij=-zwij

(8)

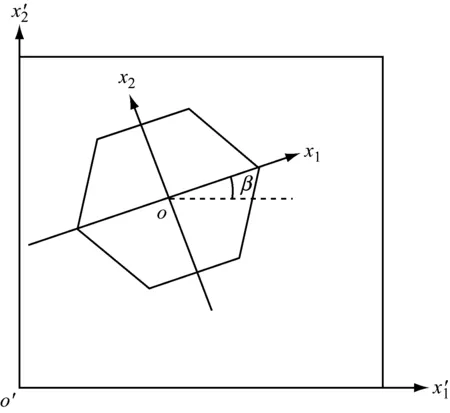
图2 螺旋形石墨烯片

1.3 非局部本构方程

基于式(4), 石墨烯片的非局部本构方程为

(9)

式中：E为石墨烯的杨氏模量；μ为泊松比。

式(9)能近似表示为

(10)

将式(6)代入式(10)中

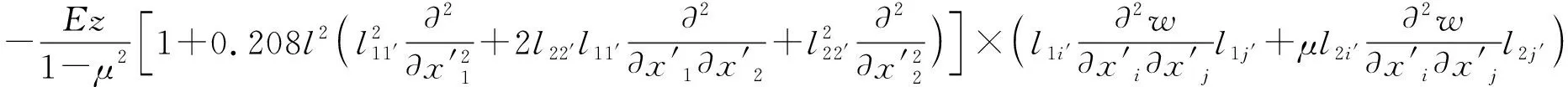
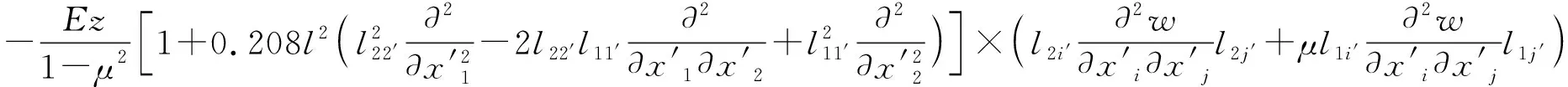
(11)

(12)

1.4 动力学方程

忽略横向剪切变形能，石墨烯片的应变能为

(13)

石墨烯片振动的动能为

(14)

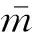
假设施加在石墨烯片上的均布力集度为q，忽略体力做功，外力做功为

Wq=∬AqwdA

(15)

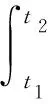
(16)

(17)

2.5 动力学方程求解

设薄板自由振动的挠度为

(18)

将式(18)代入式(16)，并且令q=0，得石墨烯片自由振动微分方程为

(19)

将动载荷展开成振型函数的级数形式

(20)

把微分方程式(16)的解答设为

(21)

将式(20)和式(21)代入式(16)得到

(22)

将式(19)代入式(22)的左边，然后比较两边的Wm的系数，得到为

(23)

常微分式(23)的解为

Tm=Amcosωmt+Bmsinωmt+τm(t)

(24)

式中：τm(t)为任一特解。

2 数值计算

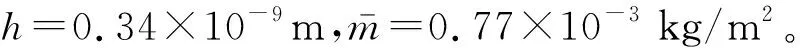
对于简支石墨烯片，其振型函数取为

(25)

将式(24)、式(25)代入式(21)，得到

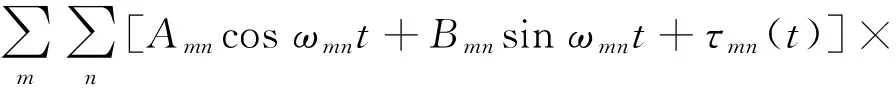
(26)

假设在石墨烯片上施加幅值为q0均布余弦动载荷。将动载荷幅值q0展开成振型函数的级数

(27)

根据三角函数的正交性，有

(28)

假设初始位移和初始速度都为0，石墨烯片的动挠度为

(29)

当l=0时，式(29)的解为石墨烯片的经典理论解。

因为基于经典连续介质力学和非局部弹性力学所得的石墨烯片的固有频率不一样，两种方法所得的最大动挠度所对应的时间点就不一样，为了研究小尺度效应，将小尺度效应定义为基于经典理论和非局部理论的石墨烯片中心点动挠度的最大值之比，即小尺度效应因子为

(30)

式中：wcd和wnd分别为基于经典和非局部理论石墨烯片中心点动挠度的最大值。

为了研究石墨烯片动力响应的小尺度效应，应用遗传算法得到时间范围为t=[0,40]×π/ωm内的中心点动挠度最大值，计算了各种长宽和螺旋角以及不同频率激励下石墨烯片动力响应的小尺度因子。

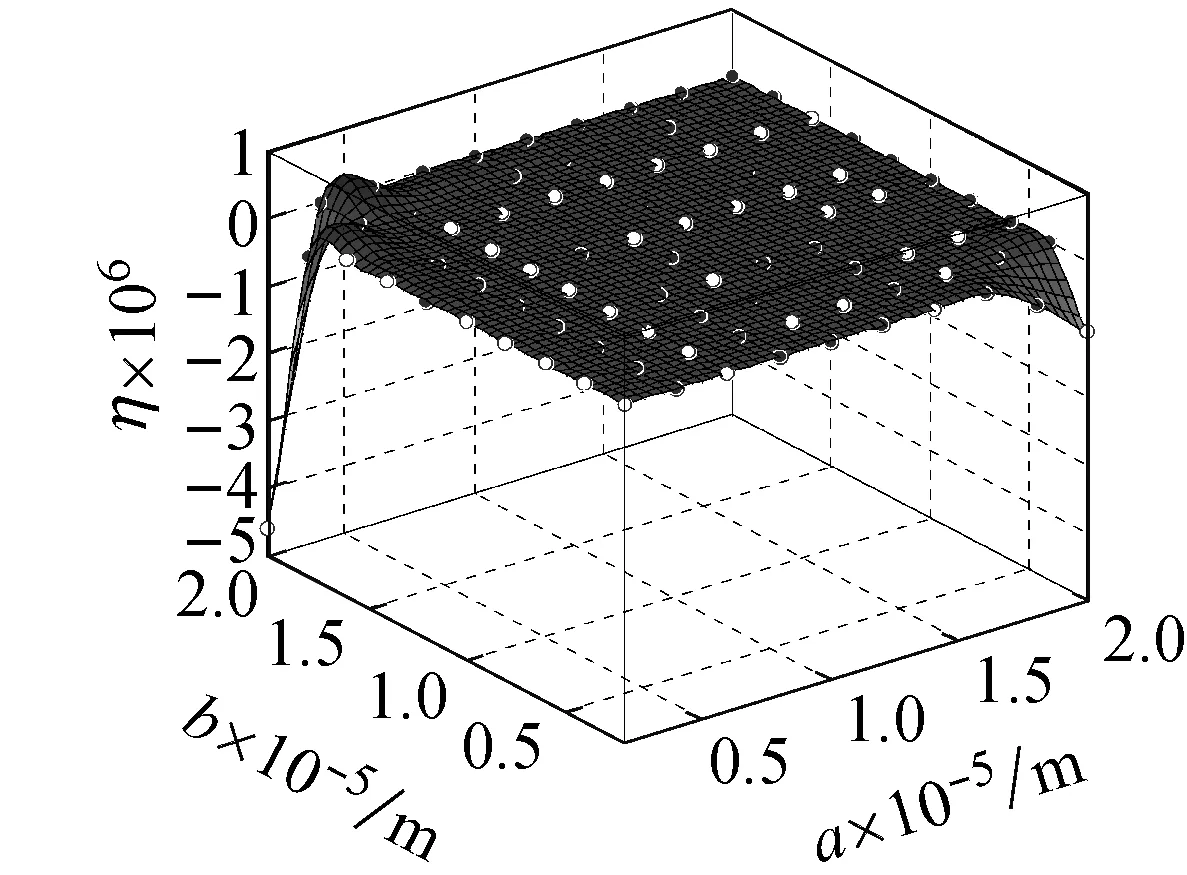
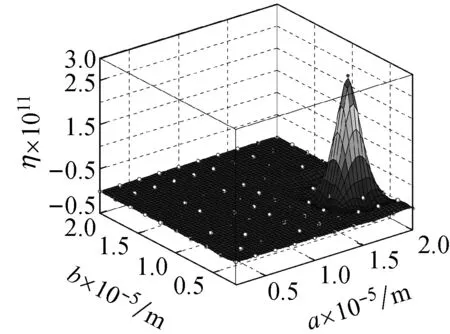
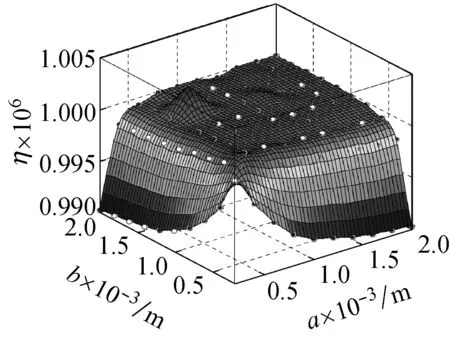
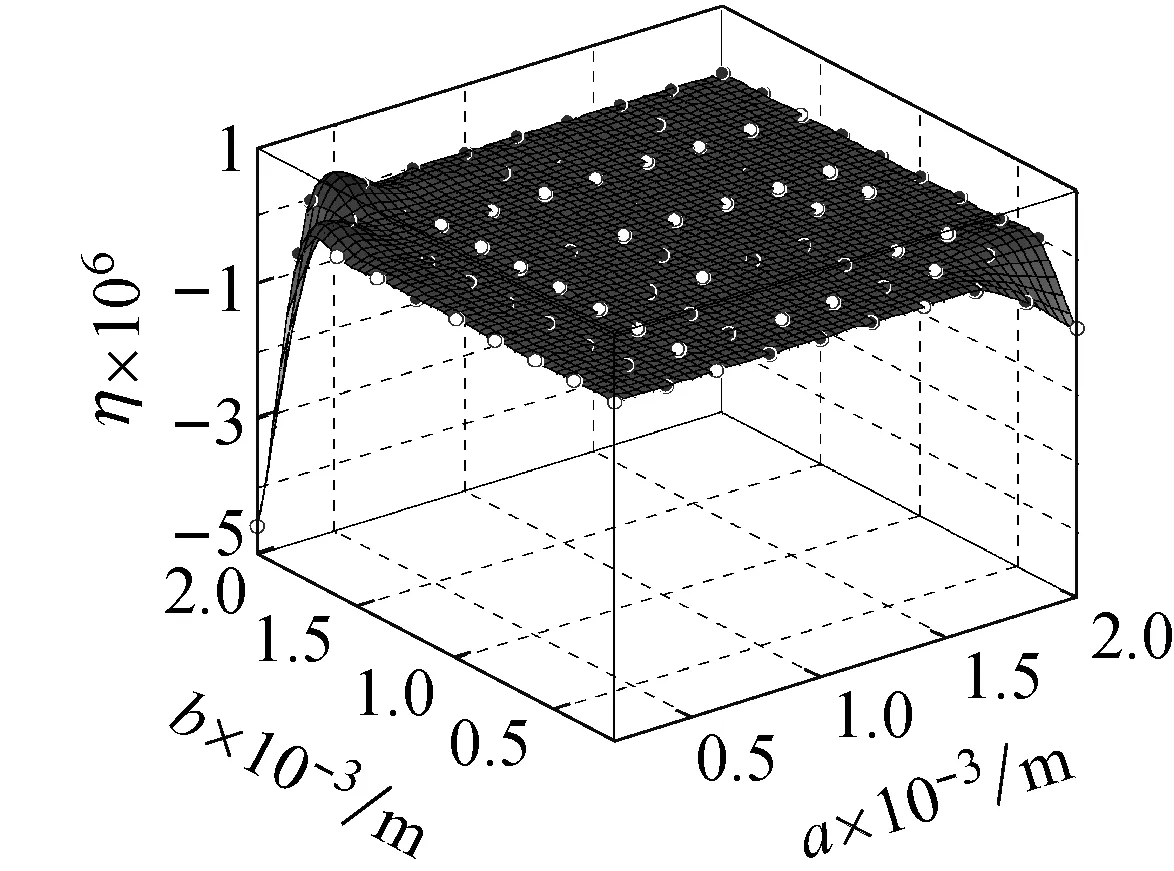
图3～图8表示在频率为ωm×107的简谐激励下，螺旋角分别为0°,π/16,2π/16,3π/16,4π/16的不同边长的石墨烯片的中心点的动挠度的小尺度因子，从图3(a)～图8(a)可以看出：当石墨烯片的长度或者宽度小于20 μm时，动力响应的小尺度效应较大，随着它的长度和宽度增大，小尺度效应减小；从图3(b)～图8(b)可以看出：当石墨烯片的长、宽都达到1 mm时，动力响应的小尺度因子接近于1，小尺度效应基本消失。我们从图3～图8的比较还发现石墨烯片的螺旋角对小尺度效应因子有很大影响，我们从式(17)可以看出，石墨烯片的螺旋角从0°变化到π/2，它的动挠度的小尺度因子关于π/4对称。从图6和图8的比较也可看出，当螺旋角为3π/16和5π/16时，石墨烯片的动挠度的小尺度因子是相同的，依此类推，螺旋角为2π/16和6π/16的石墨烯片、螺旋角为π/16和7π/16的石墨烯片以及螺旋角为0和8π/16的石墨烯片分别具有相同的挠度。

(a)

(b)

图3 螺旋角为0°的不同边长的石墨烯片的小尺度因子

Fig.3 Small size factor of graphene sheet with different side length and helical angle 0°

(a)

(b)

图4 螺旋角为 π/16 的不同边长的石墨烯片的小尺度因子

Fig.4 Small size factor of graphene sheet with different side length and helical angle π/16

(a)

(b)

图5 螺旋角为 2π/16 的不同边长的石墨烯片的小尺度因子

Fig.5 Small size factor of graphene sheet with different side length and helical angle 2π/16

为了研究激振频率对石墨烯片小尺度效应的影响，我们任意选取三个不同数量级的激励频率和螺旋角为0°的石墨烯片为研究对象，限于篇幅，其它螺旋角的石墨烯片没有列出，它们也有和螺旋角为0°的石墨烯片的一样结果。

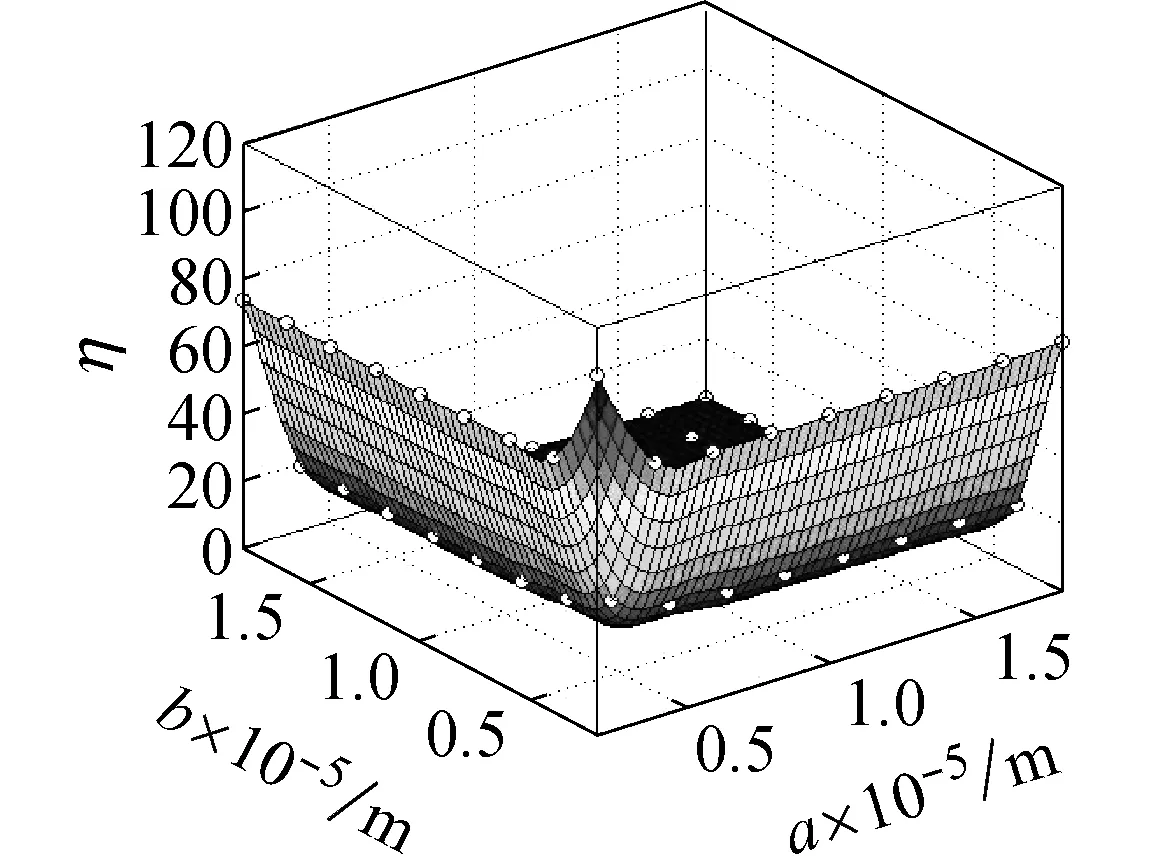
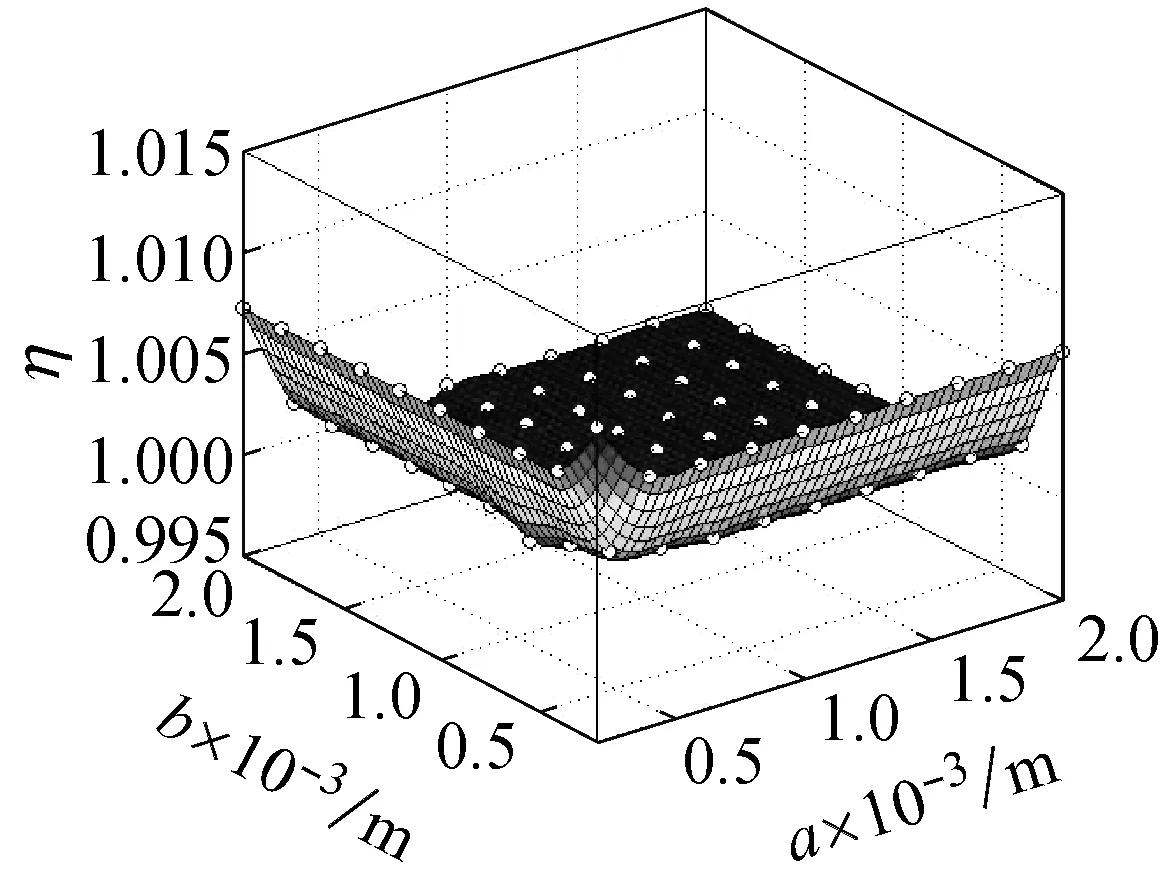
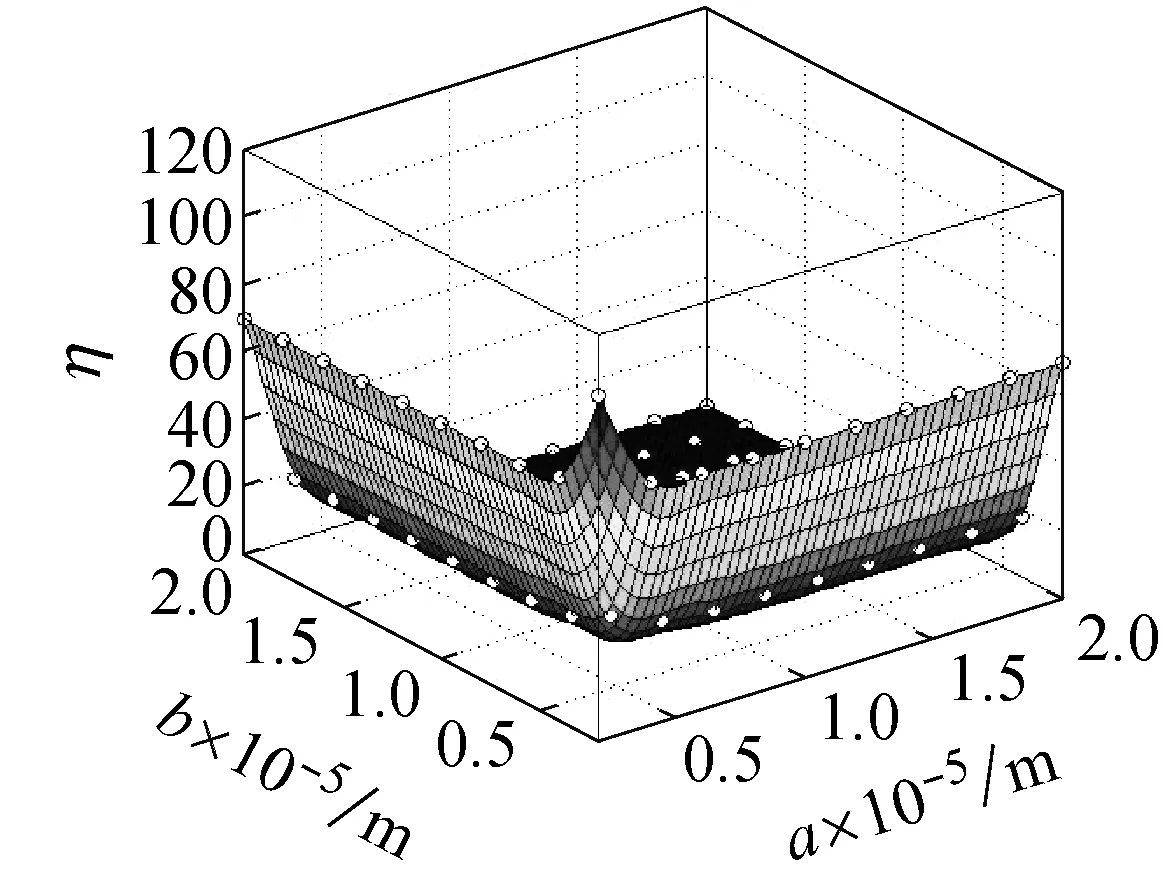
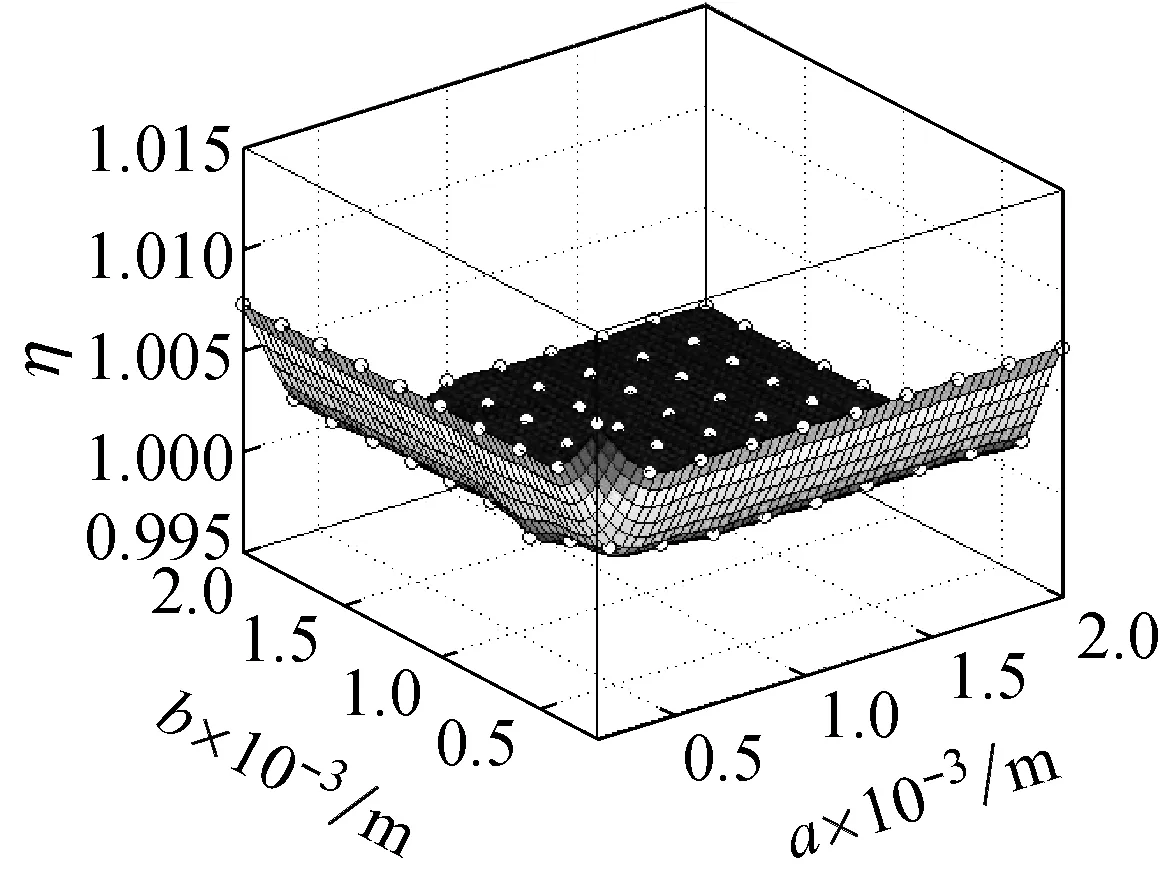
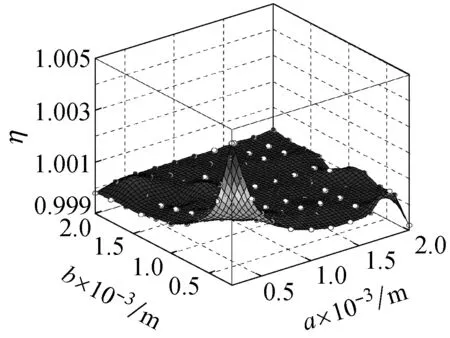
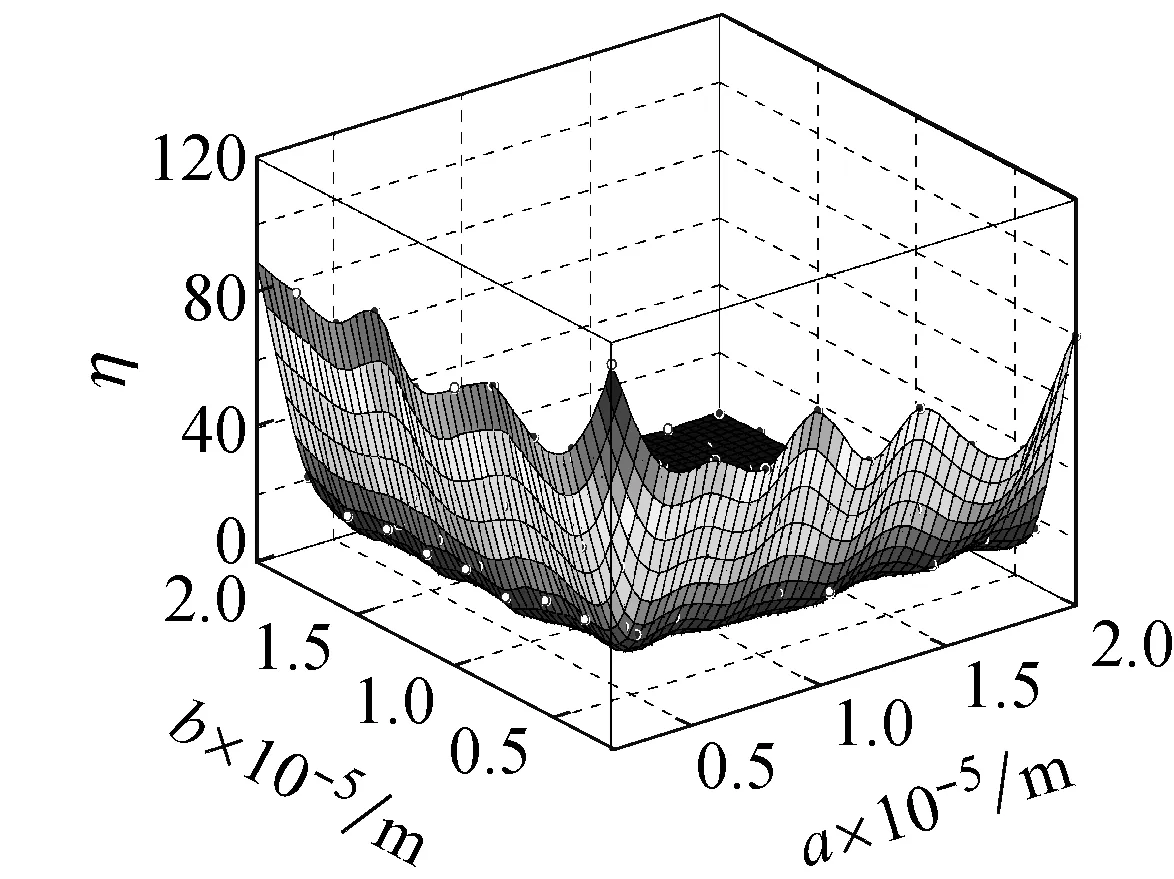
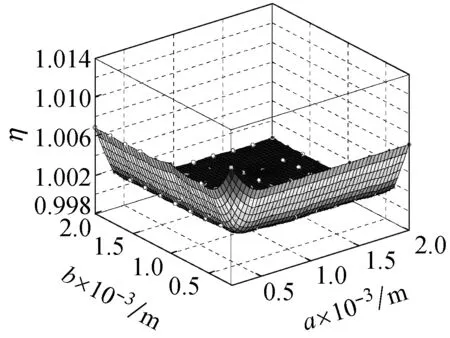
图9所示为在频率ω=ωm×10-10的简谐激励下，螺旋角为0°的不同边长的石墨烯片的中心点的动挠度的小尺度因子，从图9(a)可知，当激振力的频率为ωm×10-10时，石墨烯片的两边长都介于0.5×10-5～2×10-5m时，其小尺度效应因子介于0～120，小尺度效应十分明显。从图9(b)可知，当激振力的频率为ωm×10-10时，石墨烯片的两边长都介于0.5×10-3～2×10-3m时，其小尺度效应因子介于0.998～1.008，相比图9(a)小尺度效应明显减小。

(a)

(b)

图6 螺旋角为3π/16的不同边长的石墨烯片的小尺度因子

Fig.6 Small size factor of graphene sheet with different side length and helical angle 3π/16

(a)

(b)

图7 螺旋角为4π/16的不同边长的石墨烯片的小尺度因子

Fig.7 Small size factor of graphene sheet with different side length and helical angle 4π/16

(a)

(b)

图8 螺旋角为 5π/16 的不同边长的石墨烯片的小尺度因子

Fig.8 Small size factor of graphene sheet with different side length and helical angle 5π/16

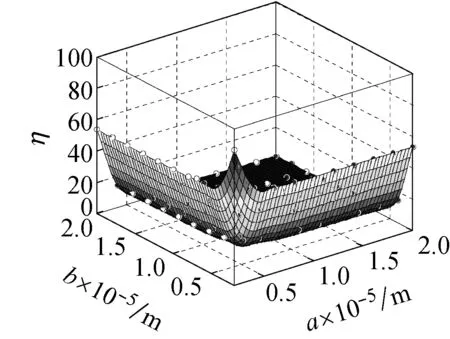
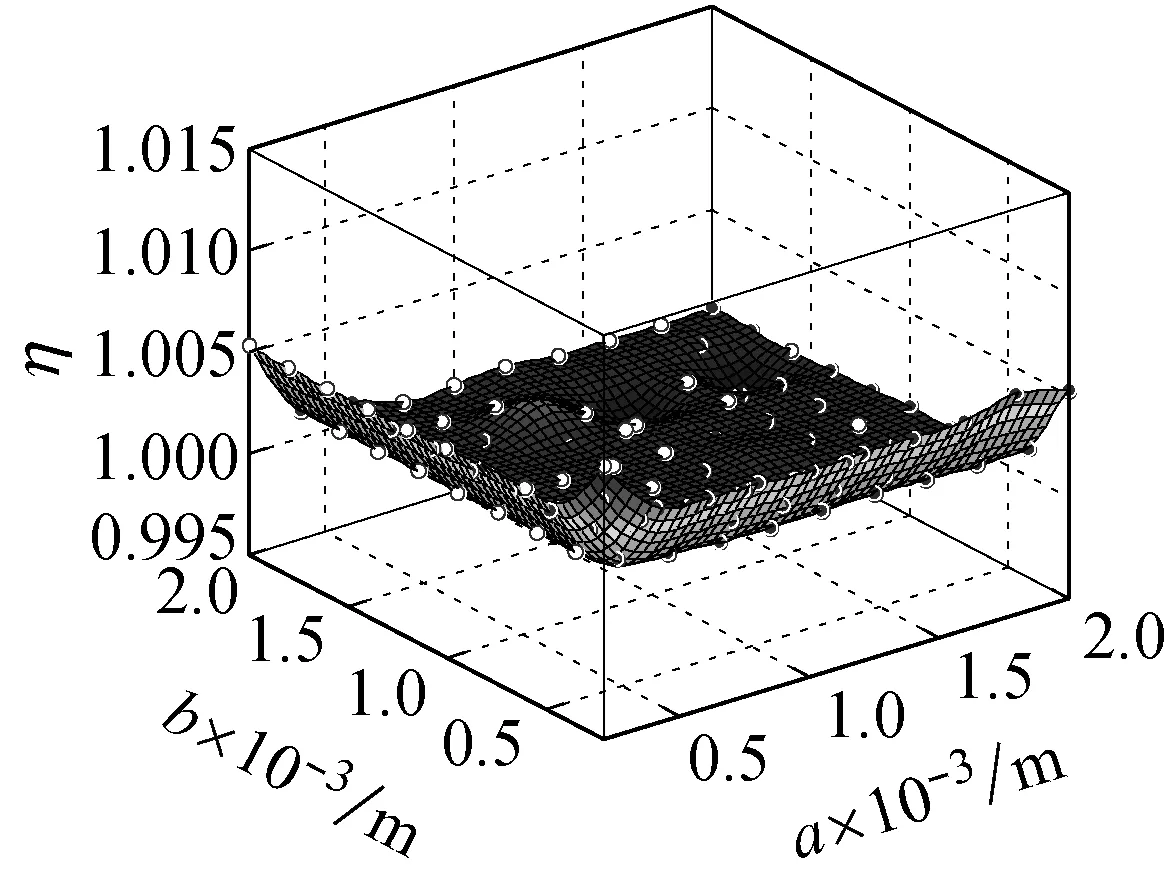
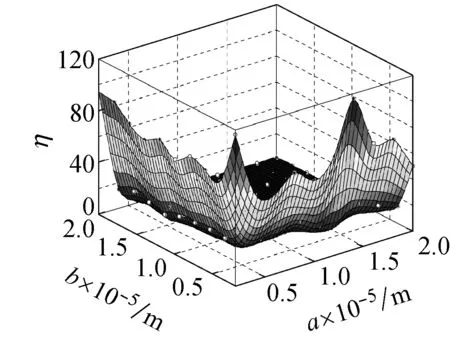
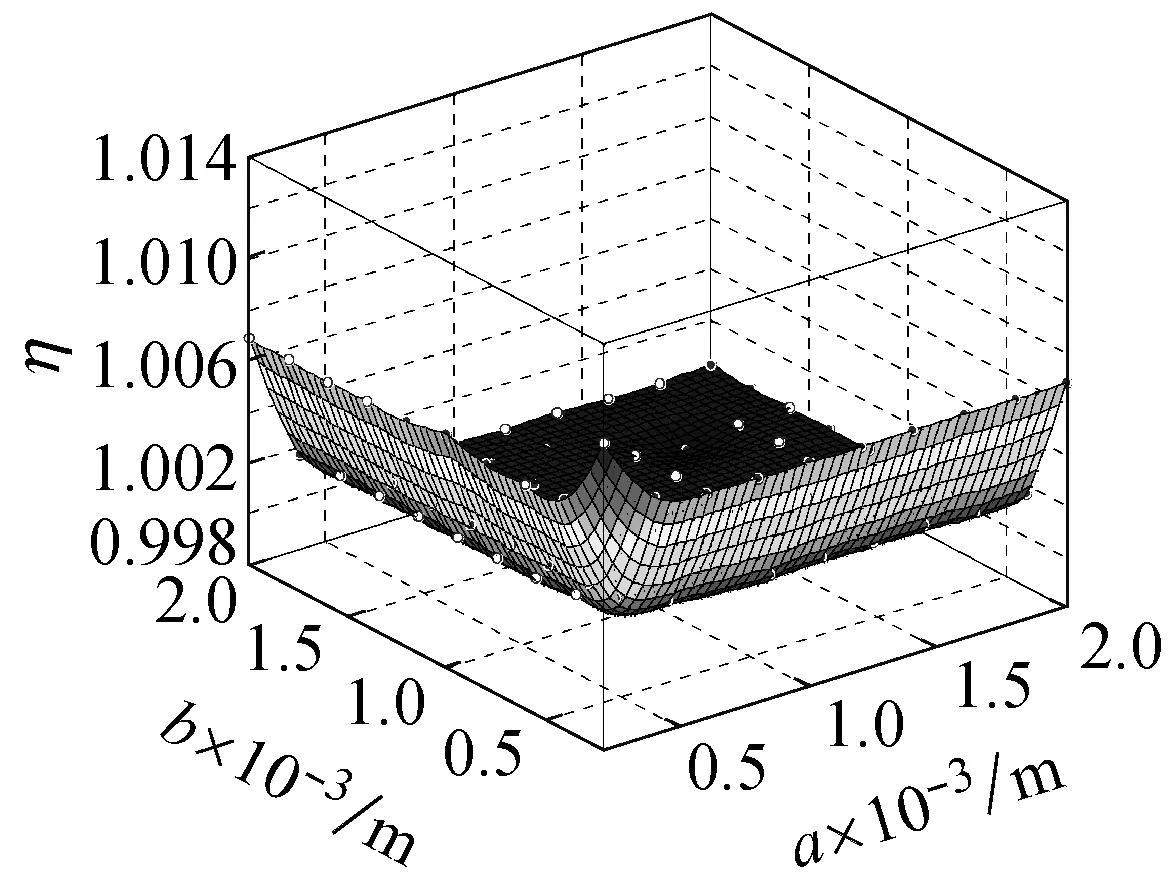
图10所示为在频率ω=ωm×103的简谐激励下，螺旋角为0°的不同边长的石墨烯片的中心点的动挠度

的小尺度因子，从图10(a)可知，在频率为ωm×103的简谐激励下，石墨烯片的两边长都介于0.5×10-5～2×10-5m时，其小尺度效应因子介于0～120之间,小尺度效应十分明显。从图10(b)可看出，当激振力的频率为ωm×103时，石墨烯片的两边长都介于0.5×10-3～2×10-3m时，其小尺度效应因子介于0.998～1.008，相比图10(a)小尺度效应明显减小。

图11所示为在频率ω=ωm×5的简谐激励下，螺旋角为0°的不同边长的石墨烯片的中心点的动挠度的小尺度因子，从图11(a)可知，在频率为ωm×5的简谐激励下，石墨烯片的两边长都介于0.5×10-5～2×10-5m时，其小尺度效应因子介于0～100。从图11(b)可看出，在频率为ωm×5的简谐激励下，石墨烯片的两边长都介于0.5×10-3～2×10-3m，其小尺度效应因子介于0.998～1.008，小尺度效应基本消失。

(a)

(b)

图9 螺旋角为0°的不同边长的石墨烯片的小尺度因子

Fig.9 Small size factor of graphene sheet with different side length and helical angle 0°

(a)

(b)

图10 螺旋角为0°的不同边长的石墨烯片的小尺度因子

Fig.10 Small size factor of graphene sheet with different side length and helical angle 0°

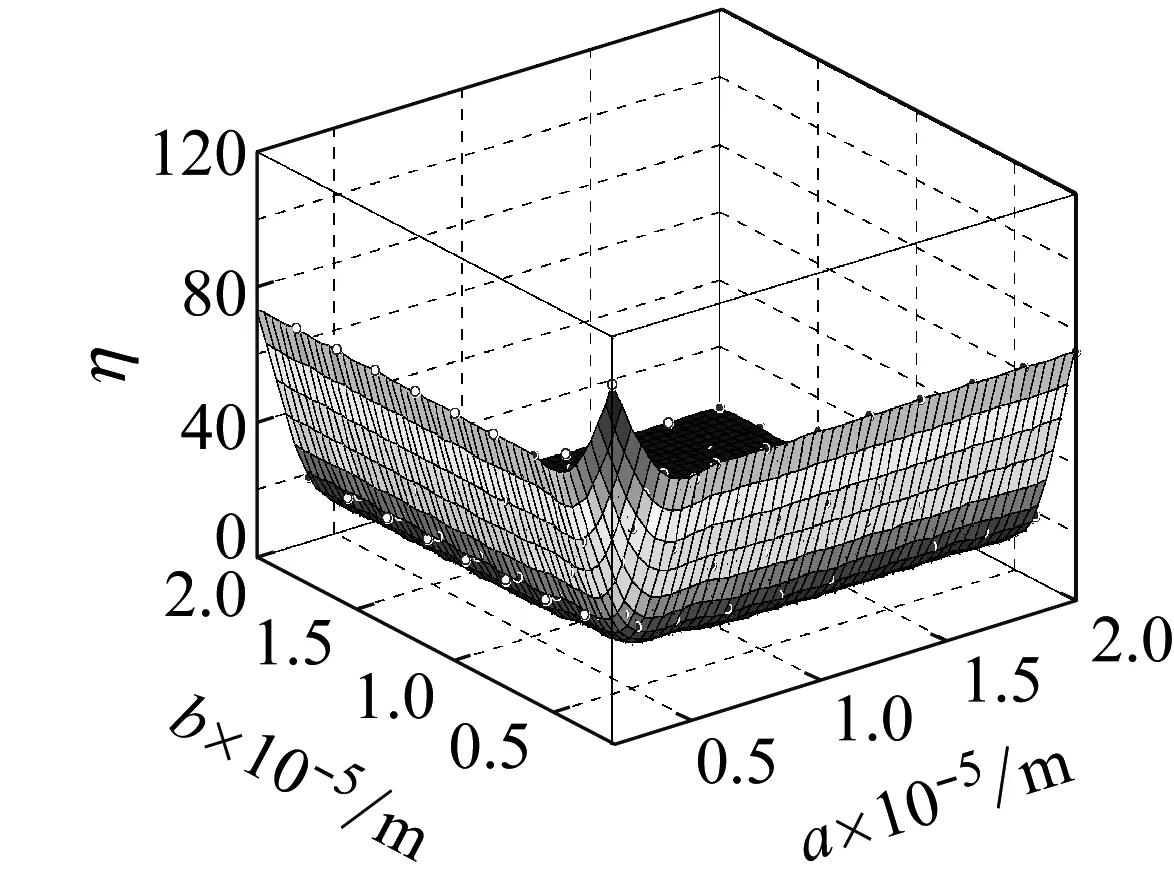
(a)

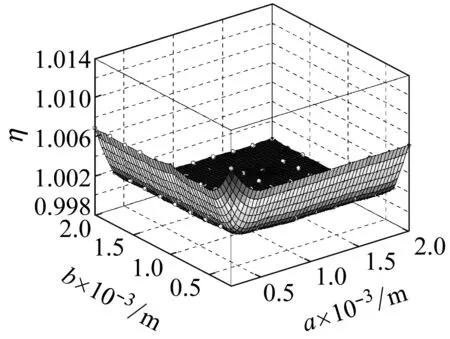
(b)

图11 螺旋角为0°的不同边长的石墨烯片的小尺度因子

Fig.11 Small size factor of graphene sheet with different side length and helical angle 0°

比较图3(a)、图9(a)、图10(a)和图11(a)可知，当石墨烯片的边长都小于2×10-5m时，小尺度因子都很大，且激振力的频率对小尺度效应的影响非常大。

比较图3(b)、图9(b)、图10(b)和图11(b)可知，当石墨烯片的边长都大于1×10-3m时，小尺度因子接近于1，且激振力的频率对小尺度效应的影响非常小，可以忽略不计。

3 结 论

基于非局部弹性理论，建立了简支石墨烯片的动力学微分方程，在初始挠度和初始速度都为0的初始条件下，对微分方程求解，得到了它的动挠度，定义了小尺度因子为基于经典理论和非局部理论的石墨烯片中心点动挠度的最大值之比，因为两种方法所得的石墨烯片的固有频率不同，所以石墨烯片中心点动挠度达到最大值所对应的时间点不同，我们应用遗传算法求得基于两种理论的最大动挠度，进而得到小尺度因子。

根据数值计算结果可以得出以下结论：

(1) 当石墨烯片的边长都小于2×10-5m时，无论激振力的频率是多大，小尺度因子都很大，小尺度效应十分明显；当石墨烯片的边长都小于2×10-5m时，激振力的频率对石墨烯片的小尺度效应有明显的影响。

(2) 当石墨烯片的两边长都大于1 mm时，小尺度因子与1十分接近，小尺度效应基本消失，且激励频率的大小对小尺度效应因子的影响很小，可以忽略不计。

(3) 石墨烯片的螺旋角对它的小尺度效应有影响，石墨烯片的螺旋角从0°变化到π/2，它的动挠度的小尺度因子关于π/4对称。