多点刚性耦合产品包装运输系统间接逆向子结构分析

孟天涯， 李明宇， 郭 栋， 王 军，3

(1. 江南大学 机械工程学院， 江苏 无锡 214122； 2. 重庆理工大学 汽车零部件先进制造技术教育部重点实验室, 重庆 400054；3. 江苏省食品先进制造装备技术重点实验室， 江苏 无锡 214122)

逆向子结构分析是通过耦合系统以及部分子结构的动态特性反求未知子结构动态特性的方法。该方法在运输包装等领域具有很高的实用价值。

在包装运输过程中，产品的损伤检测成为了一大难题，主要有以下原因：① 被包装产品的不可视性。大多数包装都不是透明的，产品破损与否不能通过肉眼实时监测到，而且材料、结构的细微变化也不是视觉可以传达的；② 不可能每次检测都要打开产品包装，这将造成极大的人力物力资源的浪费。此时，产品的振动特性作为一项重要的判定指标，在包装件的运输过程中，具有重要的损伤指示意义。在振动模态分析领域，很多研究成果已经被熟知且应用于实践，如动态子结构分析、有限元分析、模态分析等[1-2]。上述方法虽然取得了很好的发展，但针对运输包装损伤检测的特定应用条件，上述方法并不能取得突出的效果。在众多振动领域的分析方法之中，Zhen等[3-6]提出的能够从系统水平的动态特性反求部件水平动态特性的逆子结构方法，很适合运输包装过程中的损伤监测。该方法基于试验实测频响函数 (Frequency Response Function, FRF)，在中低频范围内有着优秀的预测精度，且适用于不方便拆分的耦合系统中未知子结构的动态研究。其后，Lu等[7-17]对该方法进行了修正、完善与发展。上述研究都是基于两个条件：① 组成耦合系统的子结构之间通过柔性连接相互耦合；② 系统水平的频响函数全都可以测得。然而，在实际运输过程中：① 中大型产品与运载体之间在多数情况下都是刚性连接的；② 产品与运载体的耦合界面处的空间结构一般较为复杂，使得耦合界面处的频响函数难以直接测得。逆子结构理论得到了发展[18]，讨论[19]和应用[20]，但界面传函的难测问题一直存在。王启利等[21]将虚拟质量法应用于耦合界面处频响函数的测量，解决了单点刚性耦合系统耦合界面处频响函数的测量问题，使得逆向子结构分析得以顺利进行。

本文在以上研究的基础上：① 进一步研究了多点刚性耦合系统的逆向子结构分析问题；② 提出了间接逆向子结构分析方法，无需耦合界面相关的系统水平频响函数，即可直接求得未知子结构在耦合界面处的动态特性，具有计算量小，应用方便的优点。随后针对不同的耦合系统组成，分别提出了两种不同的间接逆向子结构分析方法。最后用两种不同的集总参数模型分别代表不同的子结构构成情况，成功校验了该方法的可行性。

1 间接逆子结构理论公式

耦合系统如图1所示，由子结构A与子结构B通过多点刚性耦合在一起。

图1 耦合系统示意图

基于线性叠加原理，得到方程如下

{XS}=[HF]{FS}+[HR]{R}c(x)

(1)

式中：[HF] 为部件水平的频响函数矩阵；[HR]为子结构A和B在耦合界面处的频响函数矩阵； {FS} 为外部激励力矩阵； {R}c(x)为子结构A和子结构B之间的相互作用力矩阵； {XS}为耦合系统的位移矩阵。

系统水平动态特性的方程可写为

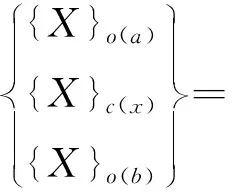
(2)

部件水平的动态特性频响函数矩阵展开为

[HF]=

(3)

(4)

其余的矩阵可展开为

(5)

{R}c(x)=[D]×

(6)

(7)

(8)

将式(2)～式(8)代入式(1)，展开得到

(9)

经式(9)可得

[HS]o(a)i(a)=[HA]o(a)i(a)-[HA]o(a)c(a)[D]×

[HA]c(a)i(a)

(10)

经变换得

[HA]o(a)i(a)-[HS]o(a)i(a)

(11)

(12)

式(12)经矩阵变换得

[HB]c(b)c(b)=

[HA]o(a)c(a)-[HA]c(a)c(a)

(13)

(2) 当[HA]o(a)c(a)和[HA]c(a)i(a)不为方阵时，式(11)等号两边分别左乘[HA]c(a)i(a)，右乘[HA]o(a)c(a)得

[HA]c(a)i(a)[HA]o(a)c(a)=[HA]c(a)i(a)×

([HA]o(a)i(a)-[HS]o(a)i(a))[HA]o(a)c(a)

(14)

经式(14)得

([HA]o(a)i(a)-[HS]o(a)i(a))[HA]o(a)c(a)×

(15)

最后整理得

[HB]c(b)c(b)=([HA]c(a)i(a)[HA]o(a)c(a))×

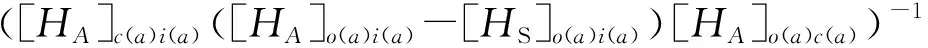
([HA]c(a)i(a)[HA]o(a)c(a))-[HA]c(a)c(a)

(16)

式(13)和式(16)即为间接逆向子结构分析公式。其中，式(13)针对已知子结构A的耦合自由度与内部自由度数量相同，式(16)针对已知子结构B的耦合自由度与内部自由度数量不同。

2 验 证

为验证多点刚性耦合系统间接逆向子结构分析公式应用于产品包装运输系统的可行性，建立模拟运输包装系统的集总参数模型如图2所示。图2(a)用于验证式(13)，图2(b)用于验证式(16)，其中，子结构B为产品，子结构A1,A2分别代表不同的运载体情况，运载体A1的耦合自由度与内部自由度数目相等(对应式(13))，运载体A2的耦合自由度小于内部自由度数目(对应式(16))。

验证步骤如下：

步骤1首先根据图2中的集总参数模型建立系统及子结构的质量、刚度、阻尼矩阵，见式(18)～式(32)。

步骤2根据频响函数的定义式(17)，将子结构A1,A2,B及系统S1,S2的质量、刚度、阻尼矩阵分别代入，求得各子结构及系统的频响函数，从而得到了产品B在耦合界面处的频响函数给定值。

(a)子结构A1内部自由度数目与耦合自由度数目相等

(b) 子结构A2内部自由度数目大于耦合自由度数目

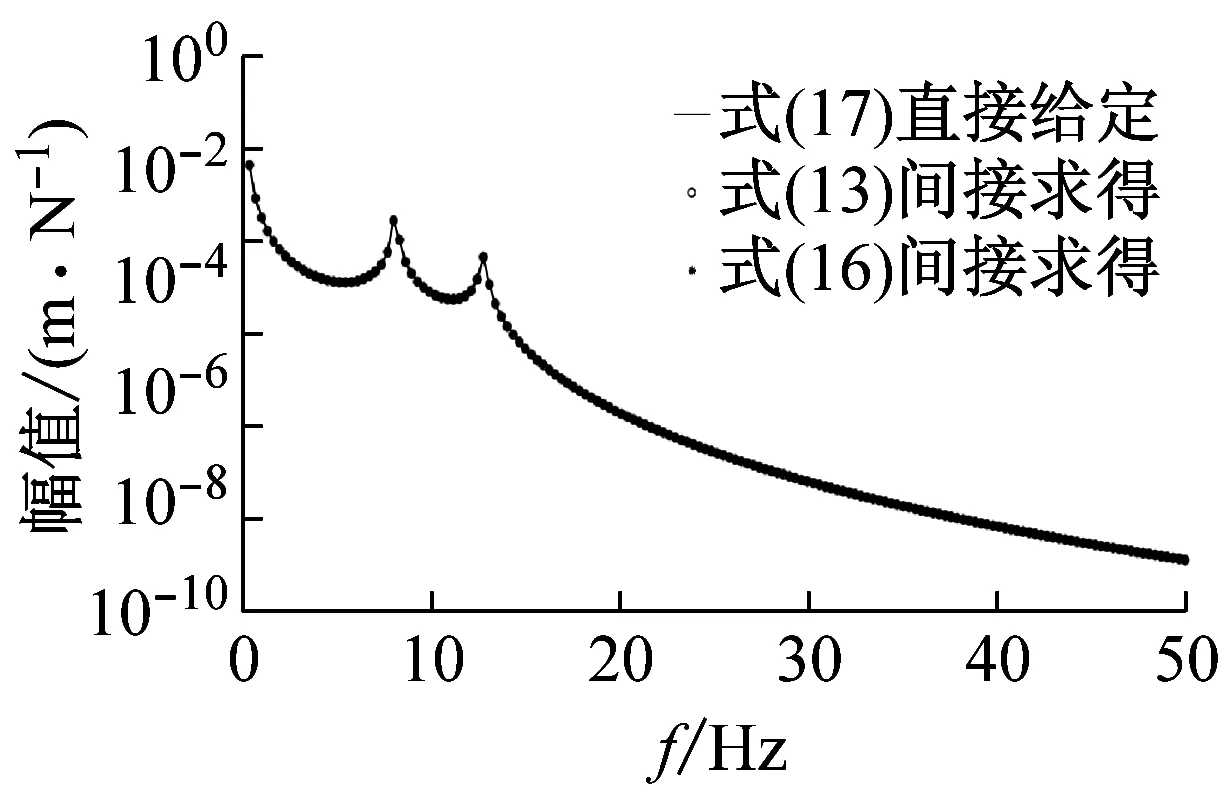
步骤3将所得频响函数分别代入式(13)和式(16)，间接预测产品耦合界面处的频响函数[HB]c(b)c(b),与直接根据式(17)给出的[HB]c(b)c(b)作对比，如图3所示。

集总参数模型的详细参数如表1所示。

(17)

(18)

(19)

表1 集总参数模型具体参数

(20)

(21)

(22)

(23)

(24)

(25)

(26)

(27)

(28)

(29)

(30)

(31)

(32)

(a) HB, c(b1)c(b1)

(b) HB,c(b2)c(b1)

(c) HB,c(b2)c(b2)

如图3所示，根据式(13)与式(16)间接求得的产品耦合界面频响函数与式(17)直接给出的频响函数完全吻合，验证了本文针对多点刚性耦合系统提出的间接逆向子结构方法的正确性。且一旦求得产品耦合界面处的频响([HB]c(b)c(b))，根据王启利的研究, 产品的所有频响都可在避免测量系统耦合界面响应的基础上获得。

3 结 论

逆向子结构分析理论在近几年取得了飞速发展，该理论能够通过系统及部分子结构的动态特性反求未知子结构的动态特性，在运输包装破损监测，机械参数辨识等方面有着重要的应用与广阔的前景。本文针对多点刚性耦合运输包装系统提出了避免测量系统耦合界面处频响函数的间接逆向子结构分析方法，解决了逆向子结构理论在应用过程中最大的难点之一。通过集总参数模型对该方法进行了校验，校验结果证明了该方法的可行性，为逆子结构理论在运输包装领域的应用提供了更大的潜力和发展空间。